Конспект урока «Возрастание и убывание функции» по алгебре для 11 класса

Муниципальное общеобразовательное учреждение

Копорская средняя общеобразовательная школа

Ленинградской области

КОНСПЕКТ УРОКА

по алгебре и началам математического анализа.

Класс: 11

Учитель: Ефремова Анна Егоровна

2012/2013 учебный год

Рано или поздно всякая правильная математическая

идея находит применение в том или ином деле.

А.Н. Крылов

Урок алгебры и начал математического анализа в 11 классе

Тема урока: Возрастание и убывание функции

Место урока: второй урок из раздела «Применение производной к исследованию функций»

Цели урока:

1. Отрабатывать навыки применения теоремы (достаточные условия возрастания и убывания функции).

2. Развивать навыки самоконтроля, внимательности; развивать мыслительную деятельность учащихся.

3. Способствовать воспитанию точности, аккуратности, уважению к труду одноклассников, ответственности за результаты своего труда и труда одноклассника.

Ожидаемые результаты (прокомментированы детям в начале урока):

• Учащиеся должны знать и уметь применять теорему о достаточных условиях возрастания и убывания для функций, заданных с помощью формулы, а также для функций, заданных графически.

Ход урока:

1. Актуализация знаний (Устная работа). Учащиеся комментируют решение, проговаривают формулы дифференцирования, а учитель записывает решение на доске.

1. Найти производную функции:

1. 

2. 

3. 

4. 

5. 

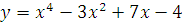
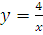
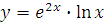
6. . Найти

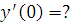
2. Решите неравенство, если .

3. На рисунке 1 изображен график функции

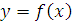
на интервале (-5; 7). (рис. 1.)

Вопросы:

• Вспомните определение возрастающей или убывающей функции на заданном промежутке.

• Назовите промежутки возрастания функции. Сколько их?

• Назовите промежутки убывания функции. Сколько их?

2. Отработка навыков применения теоремы о достаточных условиях возрастания и убывания функции по графику.

1. На рисунке 2 изображен график производной функции, 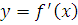на интервале (-8; 5).

Вопросы (спроецированы на доске):

• Что нужно знать, чтобы ответить по этому графику на вопросы, аналогичные предыдущим?

• Сформулируйте теорему о достаточных условиях возрастания и убывания функции.

• Как вы понимаете слова достаточные условия на интуитивно-бытовом уровне? Например, для покупки карандаша стоимостью три рубля пяти рублей достаточно, а двух рублей недостаточно.

• Кто из математиков сформулировал теорему о достаточных условиях возрастания и убывания функции? Ответ готовили дома: Великий математик Г. Лейбниц (1646-1716). В классе висит его портрет, обратить внимание детей на это. Более подробный материал можно найти на сайте uchitel.ru.

• Вспомните еще раз теорему о достаточных условиях возрастания и убывания функции. На рисунке 2 с помощью проектора появится штриховка при ответе на вопросы.

Вопросы для работы с графиком 2:

1. Сколько промежутков возрастания?

2. Назовите и покажите их.

3. Назовите длину большего промежутка возрастания.

4. Назовите длину меньшего промежутка убывания.

5. При каком значении x на отрезке [-3; -1] функция принимает наименьшее значение?

6. При каком значении x на отрезке [-6; -5] функция принимает наибольшее значение?

7. Теперь вернемся к графику 1. Назовите точки, в которых f’(x)>0, f'(x). Какую теорему нужно использовать при ответе на данный вопрос?

3. Отработка навыков применения теоремы о достаточных условиях возрастания и убывания функции, заданных формулой.

Найти промежутки монотонности функций, заданных формулами (стр. 101):

№3- 5)

№4 -4) ,

Проговаривают алгоритм исследования непрерывной функции на монотонность и записывают решение на доске и в тетрадях .

№6 a) Примечание: из учебника -дополнительный, повышенного уровня сложности, для тех учащихся, кто справился раньше. Решение данного задания можно проверить, оно есть у учителя на рабочем столе.

3. Работа в парах ( взаимопроверка, взаимооценка, взаимопомощь). «Сейчас вы отвечаете за знания друг друга. Ставите цель: устранить все пробелы в знаниях по этой теме. Задаёте вопросы друг другу, помогаете друг другу. Можно обращаться к учителю, если будут вопросы.»

Карточки даны одинакового уровня. Для тех, кто решит раньше, дается дополнительное задание №7 стр. 102 – из учебника. Его решение можно проверить, оно есть у учителя на рабочем столе.

Карточки:

1. Учебник: №4 (3) стр. 101

2. Работа с графиком по вопросам (чтение графика) –рис. 3.

На рисунке 3 изображен график функции производной функции на интервале (-6; 7).

Вопросы:

1. Сколько промежутков возрастания имеет функция ?

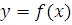2. Сколько промежутков убывания имеет функция ?

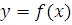3. При каком значении x на отрезке [-2; 2] функция принимает наибольшее значение?

5. Проверка работы в парах. Самоконтроль.

Задания решал одновременно ученик на обратной стороне доски. Учитель проверяет. Теперь учащиеся проверяют своё решение. (отмечают правильное решение в тетради значком «+»). Снова повторяем теорему о достаточных условиях возрастания и убывания функции.

Учитель спрашивает у учащихся, а зачем надо уметь выполнять задания, над которыми мы сегодня работаем? Ответ дети готовили дома. Теперь высказывают свои мнения.

Если не скажут, то дополнить: Многие функции, графиками которых являются кривые, описывают многие важные физические и технические процессы.

Вопрос учителя: Кто считает, что тема усвоена и можно работать над решением заданий части С из КИМов ЕГЭ? Учитель выдал задания учащимся

Задания:

Решите неравенства:

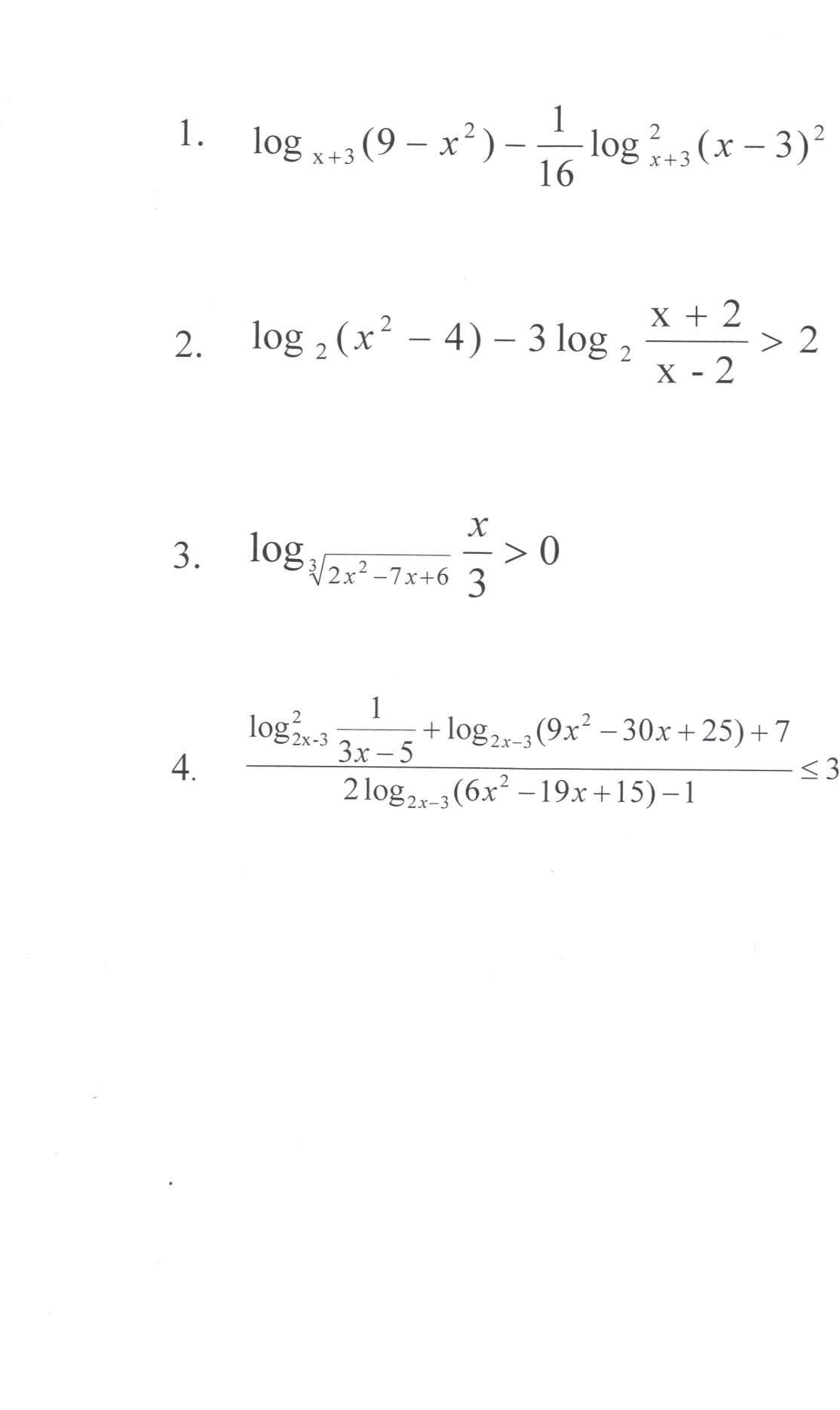
Идея решения:

1. Формулы: разность квадратов и логарифмов степени.

2. Модуль?

3. О.Д.З. помогает избавиться от модуля. Логарифм произведения.

4. Замена переменной с последующим решением рационального неравенства.

5. Учитываем О.Д.З.

Эти учащиеся работают над данными заданиями группами. Если нужна консультация учителя, то они просят об этом. Остальные учащиеся работают вместе с учителем с материалом, размещенном на сайте http://mathege.ru (открытый банк заданий ЕГЭ).

Учитель напоминает, что в Кодификаторе элементов содержания по математике для составления КИМов (код раздела 4) идет речь о тех заданиях, которые мы сегодня рассматривали. Продолжаем закреплять навыки применения достаточных условий возрастания и убывания функции. Повторяем теорему.

Используем прототипы B8 №27488, №27492, №27500.

Разбираем устно! Рассуждают с проговариванием правил.

Вопрос: Готовы ли вы поработать самостоятельно?

VI. Контроль знаний.

Самостоятельная работа: (5 мин) Если будут учащиеся, которые не готовы к самостоятельной работе, то с ними индивидуально работает учитель.

Прототипы B8 №27487, №27491, №27499.

Работы все сдают на проверку. Оценки выставляются в журнал с учетом работы в парах, индивидуальной работы.

VII. Подведение итога урока:

Сформулируем теорему. Все ли усвоили тему. Донесете ли ее до ЕГЭ.

Рефлексия.

VIII. Выдача домашнего задания:

1. Просмотреть прототипы (5) по теме урока на сайте http://mathege.ru

2. Учебник: стр. 101 №4 (2)-обязательно, стр.102 №8 (по желанию).

Список использованной литературы

1. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин]; под ред. А.Б. Жижченко. – 3-е изд. – М.: Просвещение, 2011. – 336 с.: ил.

2. Федорова Н.Е. Изучение алгебры и начал математического анализа в 11 классе: кн. для учителя / Н.Е. Федорова, М.В. Ткачева. – М.: Просвещение, 2009. – 159 с.: ил.

3. Панферов В.С., Сергеев И.Н. Отличник ЕГЭ. Математика. Решение сложных задач; ФИПИ – М.: Интеллект-Центр, 2010. – 80 с.

4. http://mathege.ru