Конспект урока «Метод интервалов» по алгебре для 10 класса
Конспект урока алгебры в 10-м классе
Сизых Галины Дмитриевны
учителя математики МБОУ
«Качульская средняя
общеобразовательная школа»
по теме
"Метод интервалов"
Место и роль урока в изучаемой теме:
данный урок второй в теме “Применение непрерывности и производной”.
Цели урока:
1. Общая дидактическая цель:
создание условий для развития и самостоятельного применения исследовательских умений учащихся, приобретения новых знаний с использованием ранее изученного материала.
2. Триединая дидактическая цель:
Образовательный аспект: создать условия для самостоятельного приобретения знаний по теме.
Развивающий аспект: развивать навыки анализа, синтеза.
Воспитательный аспект: воспитывать внимание, интерес к математике.
Формы организации учебной деятельности: индивидуальная, групповая.
Методы обучения:
исследовательский,
частично-поисковый,
репродуктивный.
Средства обучения.
Алгебра и начала анализа 10-11кл. – А.Н. Колмогоров. М: Просвещение, 2011.
Виды контроля: самоконтроль, контроль учителя.
Ход урока
-
Организационный момент.
Вводная беседа.
Пояснить правила работы с листом самоконтроля. (Приложение 1)
Плюсом отмечать те моменты, которые правильно выполнены или хорошо поняты. Где допущены ошибки или выполнено неверно – минус. Отмечать на каждом этапе, итоговую оценку поставить самим
II. Повторение:
1. Какую функцию называют непрерывной на промежутке I?
(Если функция непрерывна в каждой точке этого промежутка).
2. Сформулируйте свойство непрерывных функций.
(Если на интервале (а; в) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак).
На этом свойстве основан метод решения неравенств с одной переменной. О нём и пойдёт речь на сегодняшнем уроке.
III. Изучение нового материала.
Сообщить тему урока: «Метод интервалов»
1. Главная цель урока: научиться решать неравенства методом интервалов.
2. Пусть функция f непрерывна на интервале (а; в) и обращается в нуль в конечном числе точек этого интервала. По свойству непрерывных функций (а; в) разбивается на интервалы, в каждом из которых непрерывная функция f сохраняет постоянный знак.
Чтобы определить этот знак, достаточно вычислить значение функции f в какой-либо одной точке из каждого интервала.
3. Пример:
При рассмотрении примера записать алгоритм решения в тетрадь.
Решим неравенство 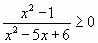
Рассмотрим функцию F(x) = 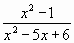
1. Найдем область определения функции:
Вся числовая прямая, кроме нулей знаменателя:
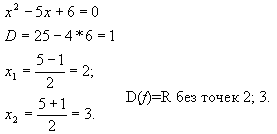
2. Найдём нули функции:
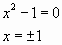
3. Отметим на числовой прямой найденные точки:

4. Определим знаки функции в каждом интервале:

Неравенство нестрогое, поэтому числа -1 и 1 (нули функции f) являются решениями неравенства.
5. Запишем ответ в виде объединения промежутков:
Ответ:
![]()
IV. Закрепление нового материала.
Тренировочные упражнения:
№ 244 (а, г)
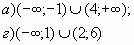
№ 245(а, б)
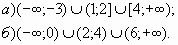
№246 (в)
![]()
№ 248 (б)
![]()
№ 249 (б)
![]()
Дополнительно: с 126 пример 2, № 243 (в)
V. . Домашнее задание.
П. 18, № 244 (б); № 245 (г); № 246 (б); № 248 (а); № 249 (в); № 243 (б, в).
Подготовиться к самостоятельной работе (Приложение 2).
VI Подведение итогов.
Учитель обобщает пройденный материал. Выполни задания:
1. Сформулируй свойство непрерывных функций.
(Если на интервале (а; в) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак)
2. Повтори план решения неравенств методом интервалов.
-
Найти область определения функции.
-
Найти нули функции.
-
Отметить на числовой прямой найденные точки.
-
Определить знаки функции в каждом интервале.
-
Записать ответ в виде объединения промежутков.
Ответьте на последний вопрос в листе самоконтроля. Оцените свою работу и сдайте листы.
Приложение 1
Лист самоконтроля
При работе на каждом этапе работы оцени свою работу:
Плюсом отметь те моменты, которые правильно выполнены или хорошо поняты. Где допущены ошибки или выполнено неверно – минус. Отметку делай на каждом этапе, итоговую оценку поставь сам(а).
| 1 вопрос | 2 вопрос | |
| Новый материал (с примером) | | |
| № 244 | а | г |
| № 245 | а | б |
| № 246 | Самостоятельно в | |
| № 248 | б | |
| № 249 | б | |
| Достиг(-ла) ли я цели урока? (подчеркни) | Да, нет | Оценка |
Приложение 2
Самостоятельная работа № 1
по теме «Метод интервалов»
-
Решите неравенство
(х-1)(х-2)(х-4)
Ответ: (-∞; 1)Ụ (2;4)
-
Решите неравенство:
(х-1)2(х-2)2(3-х)≤0
Ответ: {1;2} Ụ [3;+∞).
-
Решите неравенство:
![]() ≤0
≤0
Ответ: [1;2]Ụ(3;+∞).
4. Решите неравенство:
![]() ≥0
≥0
Ответ: [-11;2) Ụ (0;+∞).
5.Решите неравенство:
![]() ≥0
≥0
Ответ: {-2}Ụ(-1;0)Ụ(0;1)Ụ(1;2]Ụ[3;+∞).
Самостоятельная работа №2
по теме «Метод интервалов»
(Работа в группах)
Группа 1. Решите неравенства:
-
(х+3)(х+2)х(х-1)>0;
-
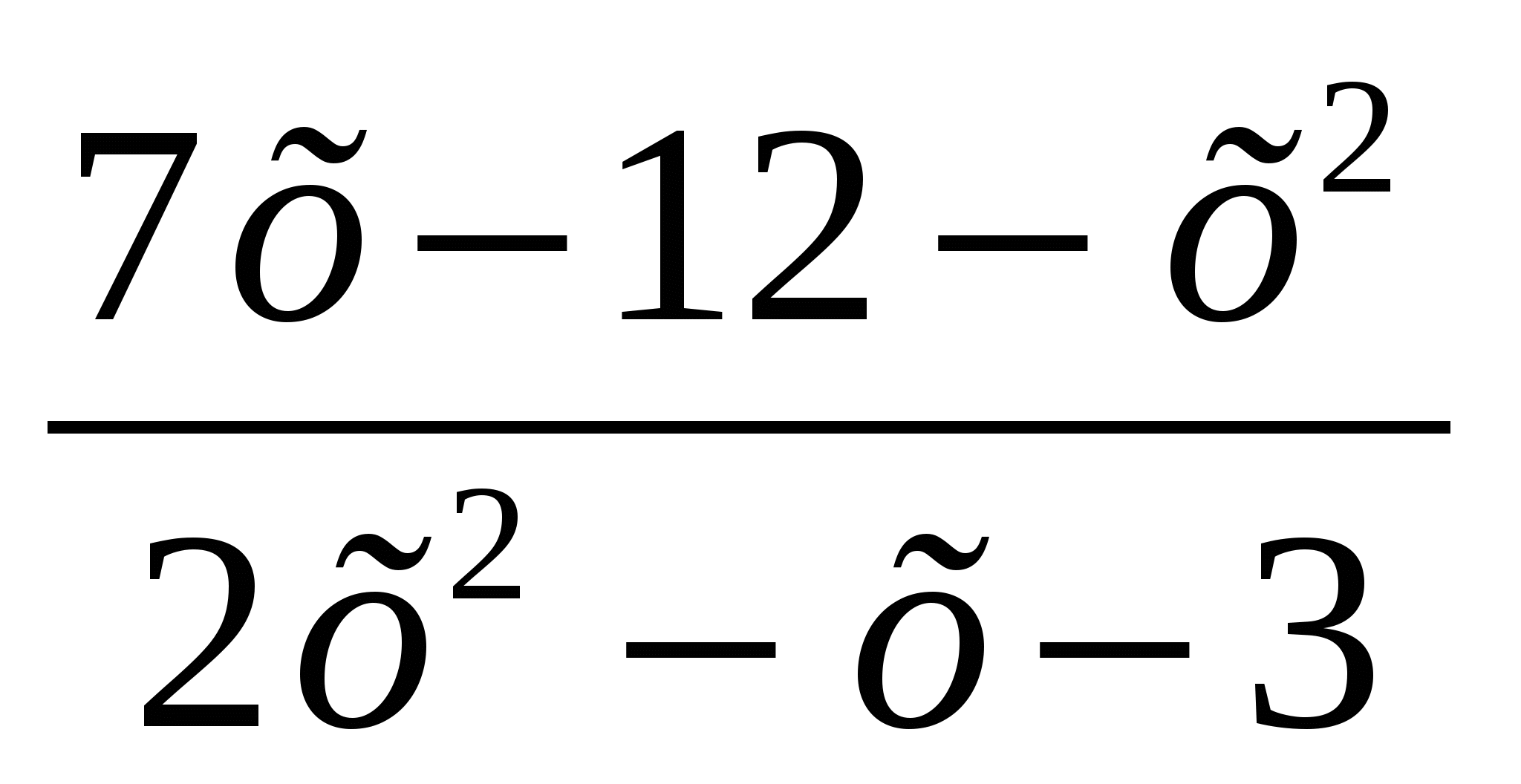
-
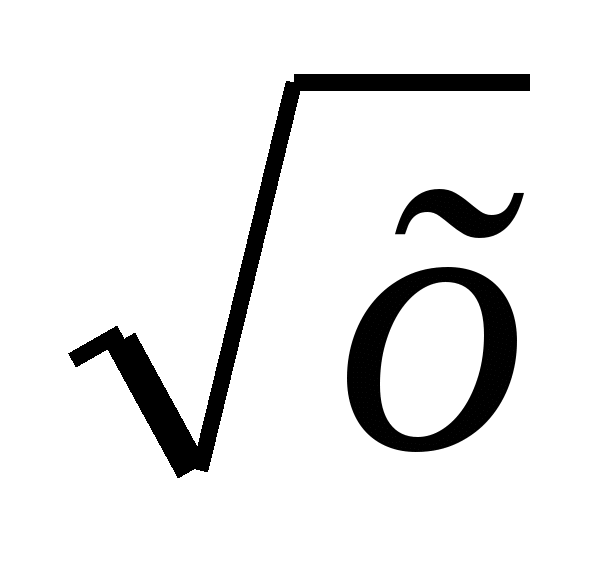 (х+2)
(х+2)
Группа 2. Решите неравенства:
1. ![]()
2. (х-3)![]()
3. (х+4)2(х+5)2(х-6)(х+3)≤0.
Группа 3. Решите неравенства:
1. ![]() ≤0;
≤0;
2. (х2-16)![]() ≤0;
≤0;
3. (х-2)3(х+1)(х-1)2(х2+2х+5)
Список использованной литературы
1 Алгебра и начала анализа 10-11кл. – А.Н. Колмогоров. М: Просвещение, 2011.
2Уравнения и неравенства в школьном курсе математики. – П.В.Чулков. М: Педагогический университет «Первое сентября»2010.
Использованные материалы и Интернет-ресурсы
Автор и источник заимствования неизвестен
Здесь представлен конспект к уроку на тему «Метод интервалов», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

