Конспект урока «Особые приёмы при решении трансцендентных неравенств методом интервалов» по алгебре для 11 класса
Павлюк Ирина Владиславовна
учитель математики
МБОУ гимназия №19 г. Липецка
Методическая разработка «Особые приёмы при решении трансцендентных неравенств методом интервалов»
Алгебра и начала анализа
11 класс
Тема урока*. Метод интервалов в решении трансцендентных неравенств.
Цели урока:
-
Выработка творческого подхода к использованию теоретического материала вообще и свойств монотонных функции в частности.
-
Овладение новым методом решения трансцендентных неравенств.
-
Развитие навыков решения неравенств.
Программно-методическое обеспечение: Математика. ЕГЭ-2006. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2005. - [1],
Математика. ЕГЭ-2009. Часть II. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2009. - [2].
План урока:
-
Постановка цели урока.
-
Разбор домашнего задания и постановка проблемы.
-
Актуализация знаний.
-
Формулирование положений нового метода.
-
Решение неравенств из домашней работы новым способом.
-
Самостоятельное (с обсуждением и корректировкой) решение неравенств.
-
Решение задач с использованием рассматриваемого метода.
-
Итоги урока и домашнее задание.
Ход урока.
-
Постановка цели урока.
В классе (раздать задания):
К пункту 6:
№2 а) ![]() б)
б) ![]() .
.
К пункту 7:
№3 Функция ![]() определена, строго возрастает и отрицательна на всей числовой прямой. Найдите все значения х, удовлетворяющие неравенству
определена, строго возрастает и отрицательна на всей числовой прямой. Найдите все значения х, удовлетворяющие неравенству
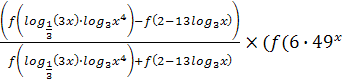 +20
+20![]() . ([1], Вариант10 С3).
. ([1], Вариант10 С3).
№4 Найдите все значения x при каждом из которых выполняется хотя бы одно из неравенств ![]() или
или ![]() ([2], Вариант5 С3)
([2], Вариант5 С3)
-
Анализ домашней работы
На предыдущем уроке учащимся было предложено в домашней работе продумать возможные пути решения неравенств:
№1 а) ![]() б)
б) ![]() .
.
№1 (а) ![]()
![]()
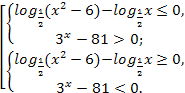
№1 (б)
![]()
![]()
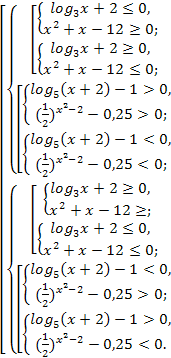
Очевидно, что решения получаются громоздкими и следует поискать другой поход.
3. Актуализация знаний.
Заметим, что множители, входящие в левые части неравенств содержат выражения, соответствующие монотонным функциям (логарифмической и показательной). Вспомним определения возрастающей и убывающей функций.
Опр.1: Функция ![]() называется возрастающей, если для
называется возрастающей, если для ![]() и
и ![]() имеет место
имеет место ![]()
![]()
![]() .
.
Опр.2: Функция ![]() называется убывающей, если для
называется убывающей, если для ![]() и
и ![]() имеет место
имеет место ![]()
![]()
![]() .
.
4. Решение неравенств из домашней работы новым способом.
№1 (а)
| Соответствующая функция | Эквивалентное выражение | Условия | |||
| f(t) | D(f) | монотонность | |||
|
|
|
| убывающая |
|
|
|
|
| R | возрастающая |
| нет |
![]()
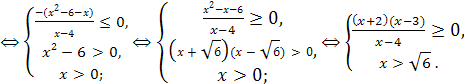
Ответ. ![]() ;3]
;3]![]()
№1 (б)
| Соответствующая функция | Эквивалентное выражение | Условия | |||
| f(t) | D(f) | монотонность | |||
|
|
|
| возрастающая |
|
|
|
|
|
| возрастающая |
|
|
|
|
| R | убывающая |
| нет |
![]()
![]()
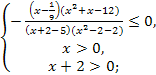
![]()
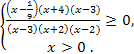
Ответ. ![]() ]
]![]()
№2 (а)
|
| |
| | |
Одз: 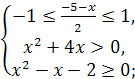
![]()
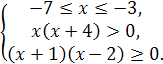 Итак,
Итак, ![]() .
.
Отметив, что при ![]() :
: ![]() , получим уравнение
, получим уравнение
![]() .
.
Функция ![]() - убывающая с
- убывающая с ![]() , функция
, функция ![]() - убывающая с
- убывающая с ![]() , функция
, функция ![]() - возрастающая с
- возрастающая с ![]() .
.
Заменив выражение ![]() на эквивалентное -(
на эквивалентное -(![]() , выражение
, выражение ![]() на эквивалентное
на эквивалентное ![]() и выражение
и выражение ![]() на эквивалентное
на эквивалентное ![]() , и учитывая Одз, получим равносильную систему:
, и учитывая Одз, получим равносильную систему:
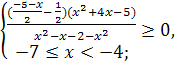
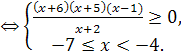
![]()
Ответ. ![]()
№2(б) ![]()
![]()
![]() .
.
Логарифмическая функция ![]() на
на ![]()
Заметим, что для существования решения неравенства необходимо выполнение условия ![]() , то есть
, то есть ![]() . А при
. А при ![]() :
: ![]() и логарифмическая функция с соответствующим основанием возрастает на своей области определения.
и логарифмическая функция с соответствующим основанием возрастает на своей области определения.
Получим равносильную систему:
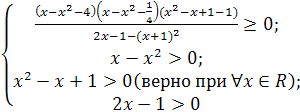
![]()
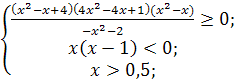 Учитывая, что
Учитывая, что ![]() и
и ![]() получим
получим ![]()
![]()
Ответ. ![]()
5. Самостоятельное (с обсуждением и корректировкой) решение неравенств.
№2 (а)
|
| |
| | |
Одз: 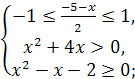
![]()
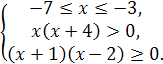 Итак,
Итак, ![]() .
.
Отметив, что при ![]() :
: ![]() , получим уравнение
, получим уравнение
![]() .
.
Функция ![]() - убывающая с
- убывающая с ![]() , функция
, функция ![]() - убывающая с
- убывающая с ![]() , функция
, функция ![]() - возрастающая с
- возрастающая с ![]() .
.
Заменив выражение ![]() на эквивалентное -(
на эквивалентное -(![]() , выражение
, выражение ![]() на эквивалентное
на эквивалентное ![]() и выражение
и выражение ![]() на эквивалентное
на эквивалентное ![]() , и учитывая Одз, получим равносильную систему:
, и учитывая Одз, получим равносильную систему:
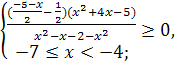
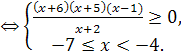
![]()
Ответ. ![]()
№2(б) ![]()
![]()
![]() .
.
Логарифмическая функция ![]() на
на ![]()
Заметим, что для существования решения неравенства необходимо выполнение условия ![]() , то есть
, то есть ![]() . А при
. А при ![]() :
: ![]() и логарифмическая функция с соответствующим основанием возрастает на своей области определения.
и логарифмическая функция с соответствующим основанием возрастает на своей области определения.
Получим равносильную систему:
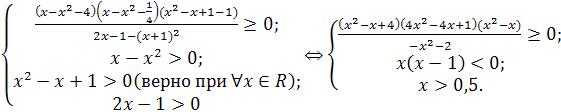 Учитывая, что
Учитывая, что ![]() и
и ![]() получим
получим ![]()
![]()
Ответ. ![]()
6. Решение задач с использованием рассматриваемого метода.
№3 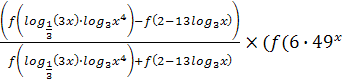 +20
+20![]() .
.
Так как по условию ![]() – возрастающая функция и
– возрастающая функция и ![]() , то можем заменить
, то можем заменить ![]() на эквивалентное
на эквивалентное ![]() , а
, а ![]() +20
+20![]() - на эквивалентное
- на эквивалентное ![]() +20
+20![]()
Кроме того по условию ![]() принимает только отрицательные значения, то
принимает только отрицательные значения, то ![]()
Получим неравенство, равносильное заданному:
![]() +20
+20![]() )
)![]()
![]() +17
+17![]() .
.
Учитывая, что ![]() +17
+17![]() при
при ![]() , получим:
, получим:
![]() ; (
; (![]() ;
; ![]() ;
; ![]() .
.
Так как ![]() - возрастающая функция с
- возрастающая функция с ![]() , то получим равносильную систему:
, то получим равносильную систему: ![]()
![]()
Ответ. [![]()
№4
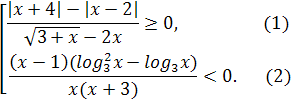
Рассмотрим неравенство (1). С учётом необходимого условия ![]() получим
получим ![]() , что равносильно совокупности
, что равносильно совокупности
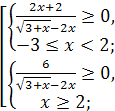
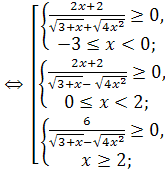
![]()
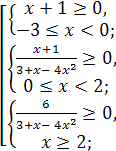
![]()
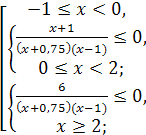
![]()
![]()
![]()
![]()
![]()
Рассмотрим неравенство (2).
![]()
![]()
![]()
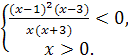
![]()
![]()
![]()
Итак, 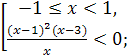
![]()
Ответ. ![]()
7. Итоги урока и домашнее задание.
№5 Найдите все значения x, удовлетворяющие неравенству ![]() , при каждом из которых выполняется хотя бы одно из неравенств
, при каждом из которых выполняется хотя бы одно из неравенств ![]() ,
, ![]() . ([2], Вариант6 С3)
. ([2], Вариант6 С3)
№6 Функция ![]() определена и строго убывает на всей числовой прямой. Найдите все значения x, удовлетворяющие неравенству
определена и строго убывает на всей числовой прямой. Найдите все значения x, удовлетворяющие неравенству
![]() . ([1], Вариант10 С3).
. ([1], Вариант10 С3).
Программно-методическое обеспечение: Математика. ЕГЭ-2006. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2005. - [1],
Математика. ЕГЭ-2009. Часть II. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2009. - [2].
* Материал рассчитан на 2 часа (сдвоенный урок)
Здесь представлен конспект к уроку на тему «Особые приёмы при решении трансцендентных неравенств методом интервалов», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.


