Презентация "Методы решения тригонометрических уравнений" (10 класс) по математике – проект, доклад
Презентацию на тему "Методы решения тригонометрических уравнений" (10 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
Методы решения тригонометрических уравнений
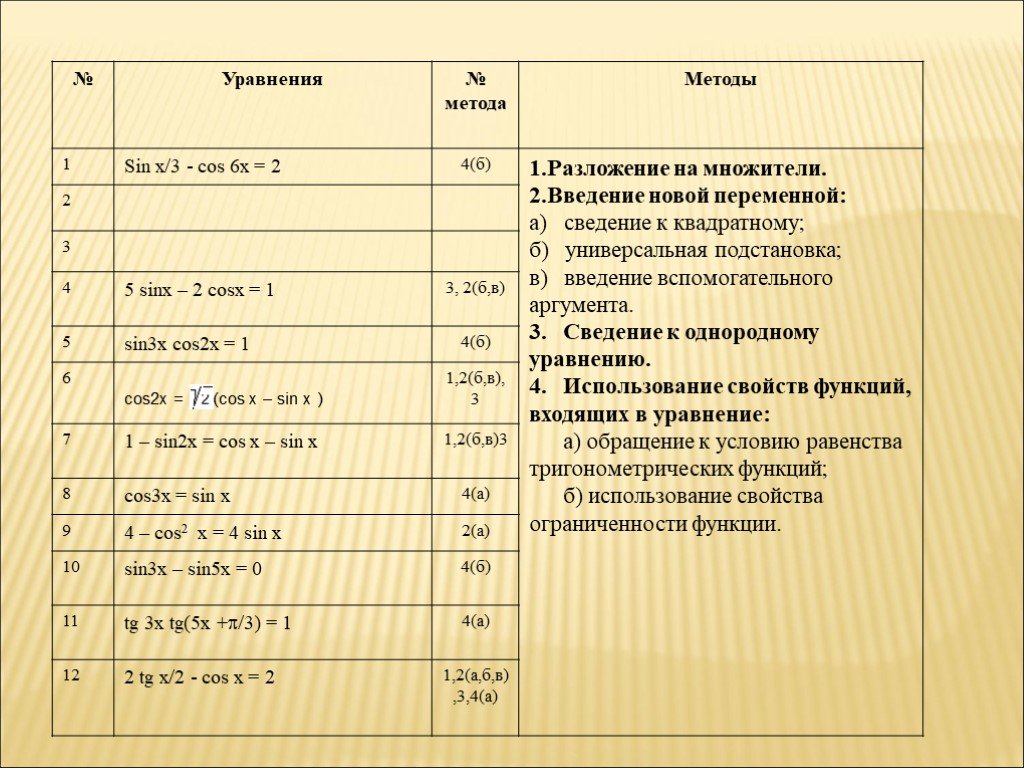
Восемь способов решения одного тригонометрического уравнения. 1.Приведение уравнения к однородному. 2.Разложение левой части уравнения на множители. ...Методы решения тригонометрических уравнений
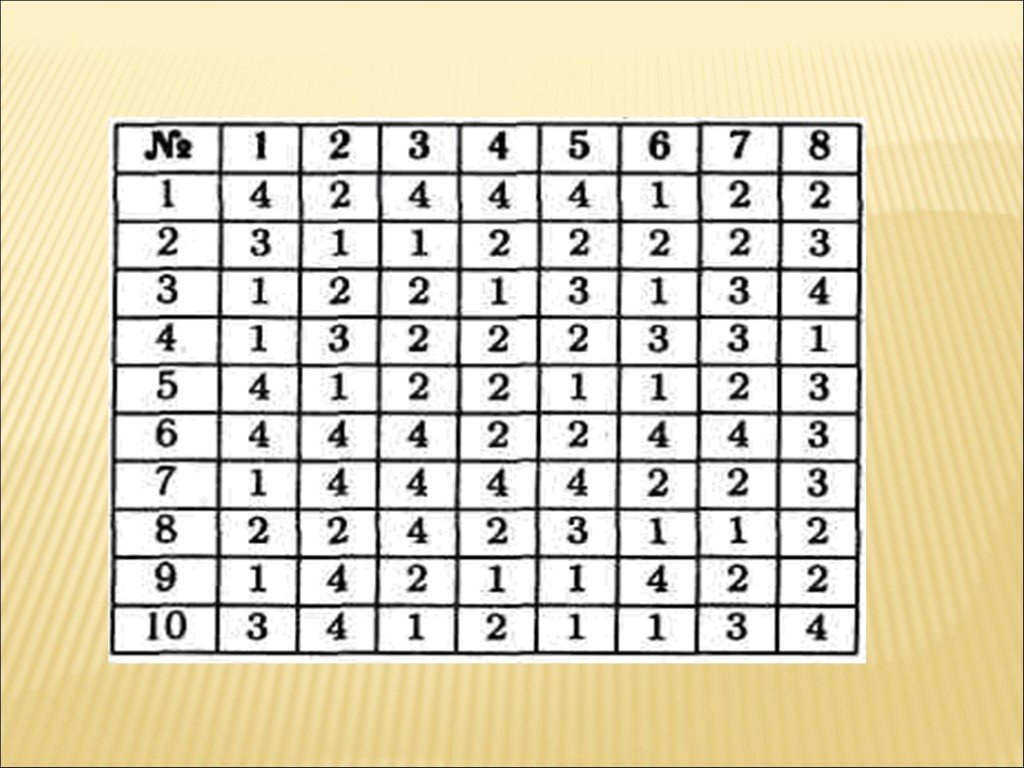
«Думай о смысле, а слова придут сами». Льюис Кэрролл. Методы решения тригонометрических уравнений Указать метод решения уравнения:. . . . . . Методы ...Методы решения тригонометрических уравнений
«Счастливый случай». 1 гейм «Разминка». 1. Решение уравнения вида cos x=a при |a| > 1? 2. При каком значении а, уравнение cos x =a имеет решения? ...Методы решения тригонометрических уравнений
«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию». Я. А. Коменский. Арксинус. ...Методы решения уравнений
Результат учения равен произведению способности на старательность. Если старательность равна нулю, то и все произведение равно нулю. А способности ...Методы решения уравнений высших степеней
Учитель математики Мурзабаева Фарида Мужавировна. Виды уравнений высших степеней. Уравнения третьей степени. Уравнения четвертой степени. Уравнения ...Аналитический и численный методы решения систем уравнений с параметром
АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...Аналитические методы решения логарифмических уравнений
Цели урока:. Обобщить и систематизировать изученные методы решения логарифмических уравнений Выявить особенности каждого метода Выяснить, всегда ли ...Методы решения уравнений с одной переменной
Тема урока: «Решение уравнений с одной переменной». Цели урока: закрепить знания и умения решений квадратных уравнений; повторить основные методы ...Общие методы решения квадратных уравнений
При решении квадратных уравнений часто применяется метод разложения на множители (с помощью вынесения за скобки общего множителя, формул сокращенного ...Параллельные методы решения систем линейных уравнений
Н.Новгород, 2005 г. Основы параллельных вычислений: Матричное умножение © Гергель В.П. 2 из 44. Постановка задачи Метод Гаусса Последовательный алгоритм ...Примеры решения тригонометрических уравнений
Примеры решения тригонометрических уравнений. Проверочная работа В заданиях 1-6 найдите значения аркфункций в заданиях 7-15 запишите решения простейших ...Методы решения систем уравнений
Под кейсом понимается несколько страниц текста, материал из учебника, различные презентации, видеоматериал. Ответ:. . . Обратимся к кейсу. Если х=0, ...Методы решения иррациональных уравнений
Метод возведения в степень.Пример 1. Ответ: 2. Пример 2. Ответ: 3. Пример 3. Метод составления смешанной системы.
Ответ: 7.
Решение уравнений ...
Методы решения систем линейных уравнений 1- ой степени
Проверка домашнего задания. Устная работа. Какие способы решения систем линейных уравнений мы знаем? Сколько их? Какой из способов самый наглядный? ...Методы решения систем линейных уравнений с двумя переменными
Инженер-электрик: "Это уравнения напряжения или токов в электрической цепи с активными сопротивлениями." Инженер-строитель: "Это уравнения, связывающие ...Методы решения логарифмических уравнений
Цель:. Систематизировать знания учащихся о решении логарифмических уравнений. Сформировать умения решать логарифмические уравнения. Показать возможности ...Методы решений тригонометрических уравнений
Цели урока:. Рассмотреть тригонометрические уравнения, решаемые с помощью: понижения степени введения вспомогательного угла и др. Разминка. Arcsin(a), ...Методы решения логарифмических уравнений
Задачи урока распределяются по 3 уровня:. 1 уровень – уметь решать простейшие логарифмические уравнения, применяя определение логарифма, свойства ...Общие методы решения уравнений
Обобщение и систематизация знаний об общих методах решения логарифмических, показательных, иррациональных и тригонометрических уравнений. Развитие ...Конспекты
Методы решения тригонометрических уравнений
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 5 с углубленным изучением отдельных предметов. городского ...Методы решения тригонометрических уравнений
МОУ «Ангоянская средняя общеобразовательная школа». Открытый урок. по алгебре и началам анализа. 10 класс. Тема:. Методы решения тригонометрических ...Общие методы решения тригонометрических уравнений
. ГБОУ ООШ с. Малое Ибряйкино. Похвистневского района Самарской области. Конспект урока для 10 класса на тему. «Общие методы ...Основные методы решения тригонометрических уравнений
. МАТЕМАТИКА 11 класс. Тема: Основные методы решения тригонометрических уравнений. Цели урока:. Обобщить и систематизировать полученные знания ...Общие методы решения тригонометрических уравнений
. Муниципальное общеобразовательное учреждение. Малоибряйкинская основная общеобразовательная школа. Похвистневского района Самарской области. ...Виды уравнений. Методы решения уравнений
ГАОУ НПО Профессиональный лицей № 59. Оренбургская область, Красногвардейский район, с. Плешаново. Виды уравнений. Методы решения уравнений. ...Общие методы решения логарифмических и показательных уравнений
11 класс. Тема урока: Общие методы решения логарифмических. и показательных уравнений. Веками люди над их открытием трудились, Показательная ...Методы решения иррациональных уравнений
Урок семинар - практикум в 11-м классе по алгебре и началам анализа. Тема: «Методы решения иррациональных уравнений». Цели и задачи урока:. . ...Методы решения уравнений и неравенств
Тема: «Методы решения уравнений и неравенств». 9 класс. ГБОУ СОШ №1968. Учитель математики: Осина И.В. Г.Москва. Тип урока. :. Урок обобщения ...Методы решения квадратных уравнений
Организационная информация. . . Тема урока. . Квадратные уравнения: методы решения. . . Предмет. . Алгебра. . . Класс. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 июня 2019
Категория:Математика
Классы:
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию