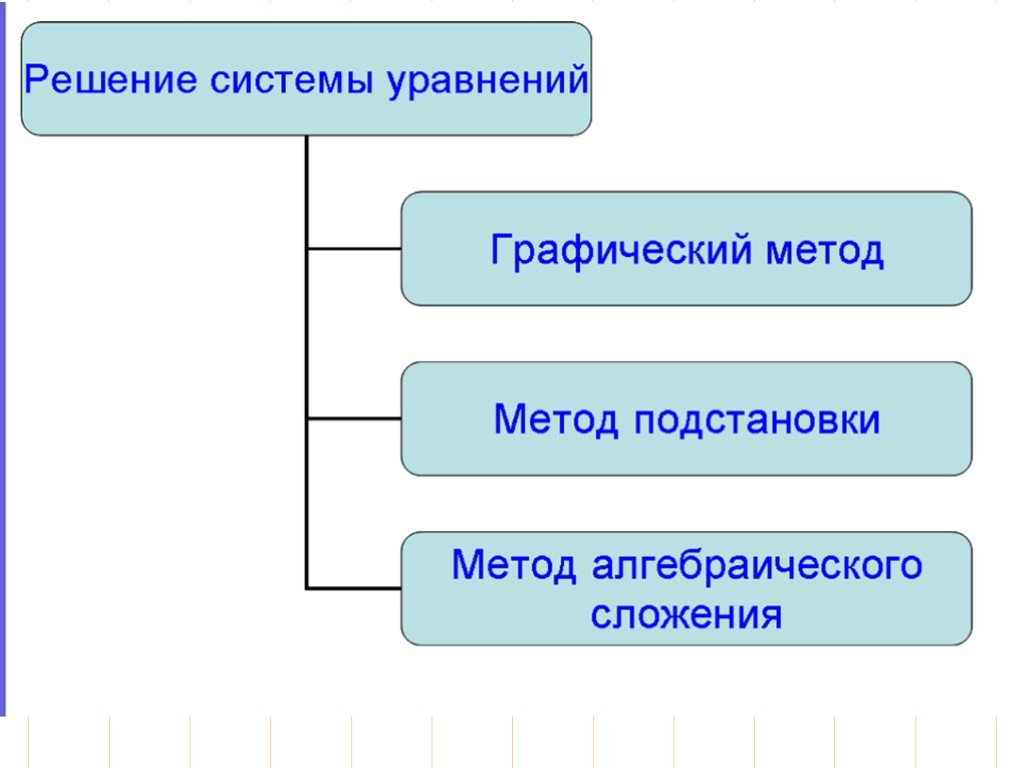
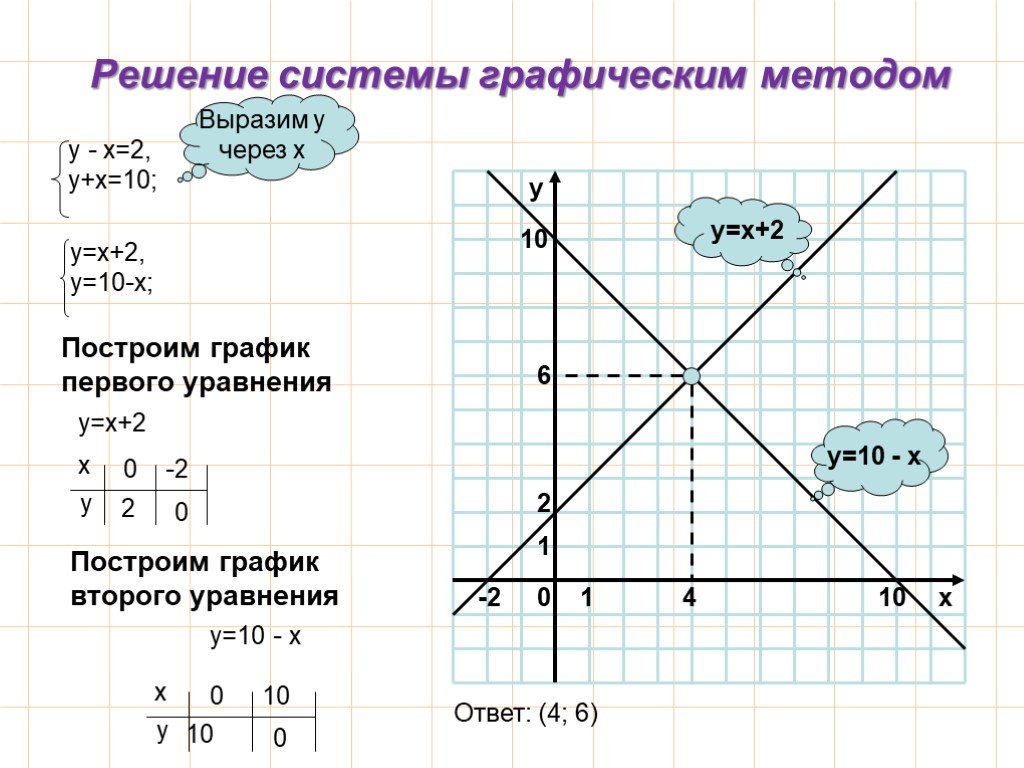
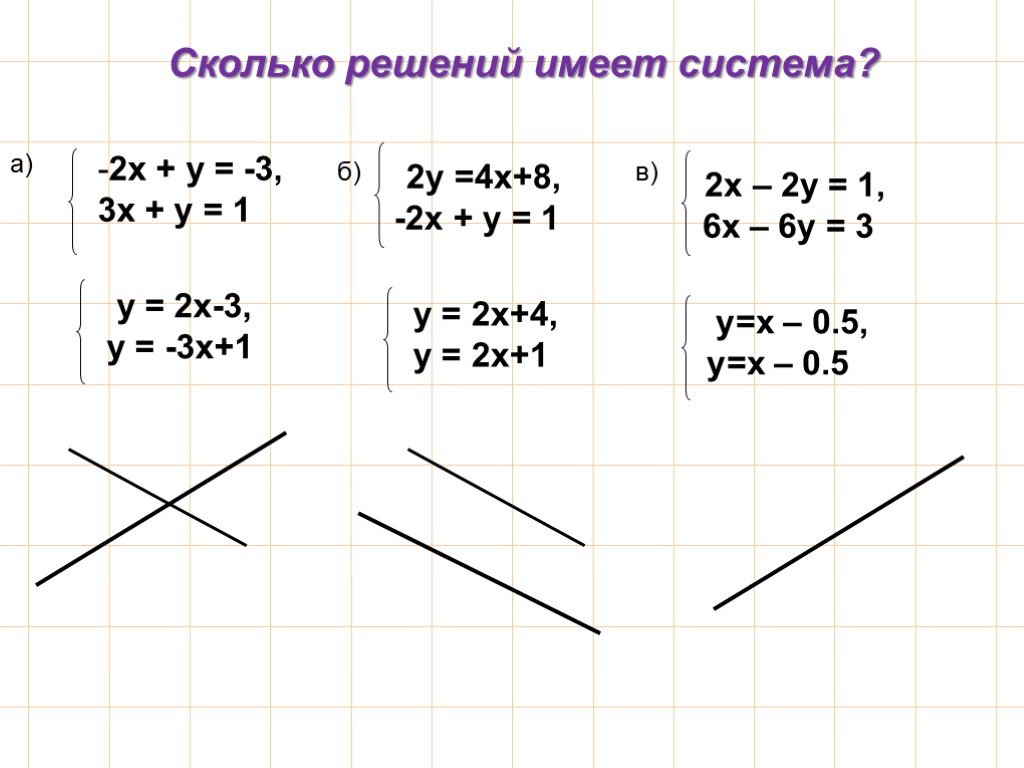
Презентация "Методы решения систем линейных уравнений с двумя переменными" по математике – проект, доклад
Презентацию на тему "Методы решения систем линейных уравнений с двумя переменными" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).
Слайды презентации
Список похожих презентаций
Аналитический и численный методы решения систем уравнений с параметром
АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Аналитические методы решения логарифмических уравнений
Цели урока:. Обобщить и систематизировать изученные методы решения логарифмических уравнений Выявить особенности каждого метода Выяснить, всегда ли ...10 способов решения квадратных уравнений
История развития квадратных уравнений. Квадратные уравнения в Древнем Вавилоне: Х2+Х=3/4 Х2-Х=14,5. Как составлял и решал Диофант квадратные уравнения. ...8 класс "Решение квадратных уравнений"
. . . . . . «Уравнение – это золотой ключ, открывающий все математические тайны». . Цель: привести в систему знания о квадратных уравнениях и умение ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...7 способов решения тригонометрического уравнения
Математики видят ее в:. гармонии чисел и форм, геометрической выразительности, стройности математических формул, решении задач различными способами, ...Алгоритм решения неравенств
Для любых двух простейших чисел а и в выполняется одно из двух условий: либо а больше в (а>в), либо а меньше в (а. Возникает задача: найти все – значения ..."Взаимное расположение прямых в пространстве. Угол между двумя прямыми
«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия». Дьердье Пойа, венгерский математик. ...Алгоритмы с ветвлениями
Найди ошибку. Вставить ключ в замочную скважину. Достать ключ из кармана. 3. Вынуть ключ. 4. Повернуть ключ два раза против часовой стрелки. Найди ...Алгоритмы работы с величинами
Цель:. Познакомиться с понятием «величина» и показать ее назначение в программировании. 1. Как называется алгоритм, записанный на «понятном» компьютеру ...Алгоритмы внутренних точек с приближенным решением вспомогательной задачи
1939 – линейное программирование (Канторович). 1947 – симплекс-метод (Данциг). 1967 – метод внутренних точек (Дикин). 1984 – полиномиальный МВТ (Кармаркар). ...Алгоритм с ветвлениями и циклами.
Линейный алгоритм. "Соберись в школу" Начало Конец Встань Умойся Сделай зарядку Оденься Позавтракай Собери портфель. Ветвление. "Раскрась крышу дома". ...«Действия с обыкновенными дробями (2)»
Урок по теме «Действия с обыкновенными дробями». На острове Дробей. 1. Сократите дроби. 2. Исключите целую часть из числа. 3. Переведите число в неправильную ...Алгебраические дроби с разными знаменателями
Повторить правила сложения и вычитания числовых дробей с разными знаменателями; Изучить правила сложения и вычитания алгебраических дробей с разными ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ..."Все действия с обыкновенными дробями"
Великие открытия ученых математиков ХХ века. «Математика является значительно большим, чем наука, поскольку она является языком науки». Нильс Бор, ...«Действия с дробями»
Цели урока:. Устный счет. Какая часть каждой фигуры окрашена? Есть ли на чертежах ошибки? Найдите их и назовите ошибку. Нет ли в чертежах ошибок? ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...«Закрепление изученого» (Сложение и вычитание с переходом через десяток в пределах 20)
Цели урока:. 1. Закрепить знания о сложении и вычитании с переходом через десяток в приделах 20. 2. Упражняться в решении задач изученных видов. План ...Конспекты
Виды уравнений. Методы решения уравнений
ГАОУ НПО Профессиональный лицей № 59. Оренбургская область, Красногвардейский район, с. Плешаново. Виды уравнений. Методы решения уравнений. ...Взаимное расположение графиков линейных функций
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа №10. Урок алгебры для 7 класса. «Взаимное расположение ...Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Взаимное расположение графиков линейных функций
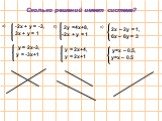
Тема:. Взаимное расположение графиков линейных функций. Тип урока. : Совершенствование знаний, умений, и навыков. Цели урока:. Выяснить ...Виды тестов и способы их решения
2.5 Конспект урока с аспектным анализом. Тема: Виды тестов и способы их решения. Цель:. - познакомить учащихся с целью проведения ЕГЭ по математике;. ...Взаимное расположение графиков линейных функций
ПЛАН-КОНСПЕКТ УРОКА Конспект урока по теме: «Взаимное расположение графиков линейных функций». . ФИО (полностью). . Чичерова Татьяна ...Взаимное расположение графиков линейных функций
Муниципальное образовательное учреждение средняя общеобразовательная школа № 33 с углубленным изучением отдельных предметов. Дзержинского района ...Взаимное расположение графиков линейных функций
Тема урока: « Взаимное расположение графиков линейных функций». Цель урока:. закрепить умения и навыки нахождения углового коэффициента, познакомить ...Взаимное расположение графиков линейных функций
Учитель: Короленко Евгения Николаевна. Конспект урока по алгебре 7 класса. Тема «Взаимное расположение графиков линейных функций». Цели:. Образовательные:. ...Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций. Учитель: Мисник И.Ю., г Уссурийск. Тип урока: изучение нового материала. Цели урока:. Образовательная. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:7 февраля 2019
Категория:Математика
Содержит:25 слайд(ов)
Поделись с друзьями:
Скачать презентацию