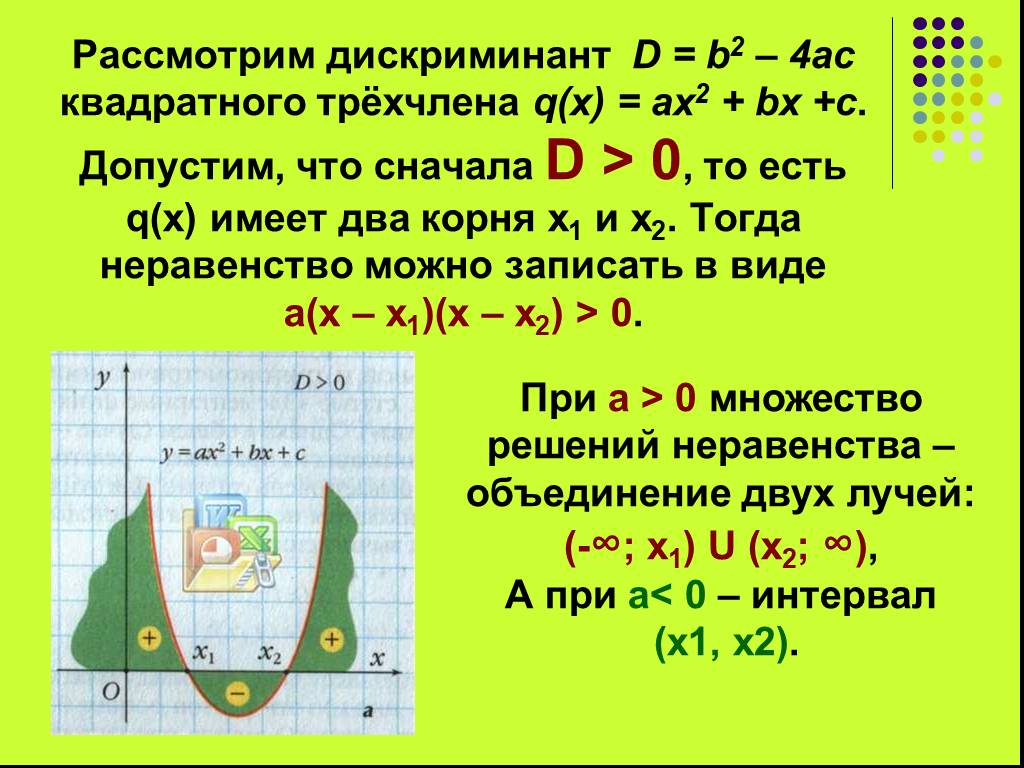
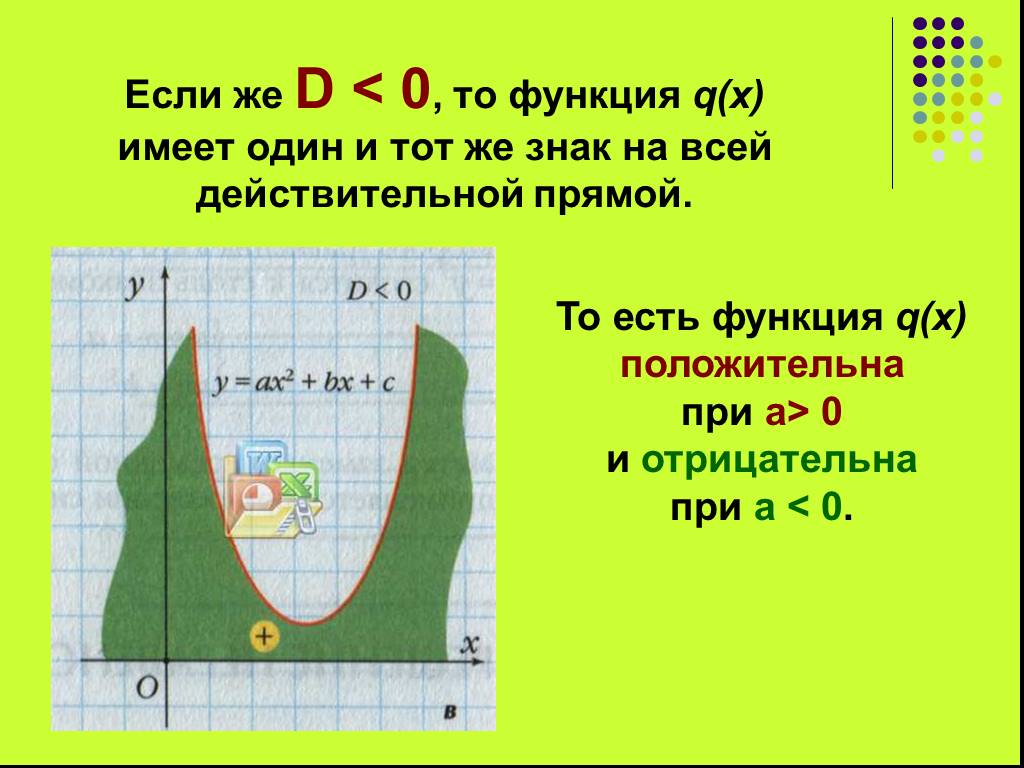
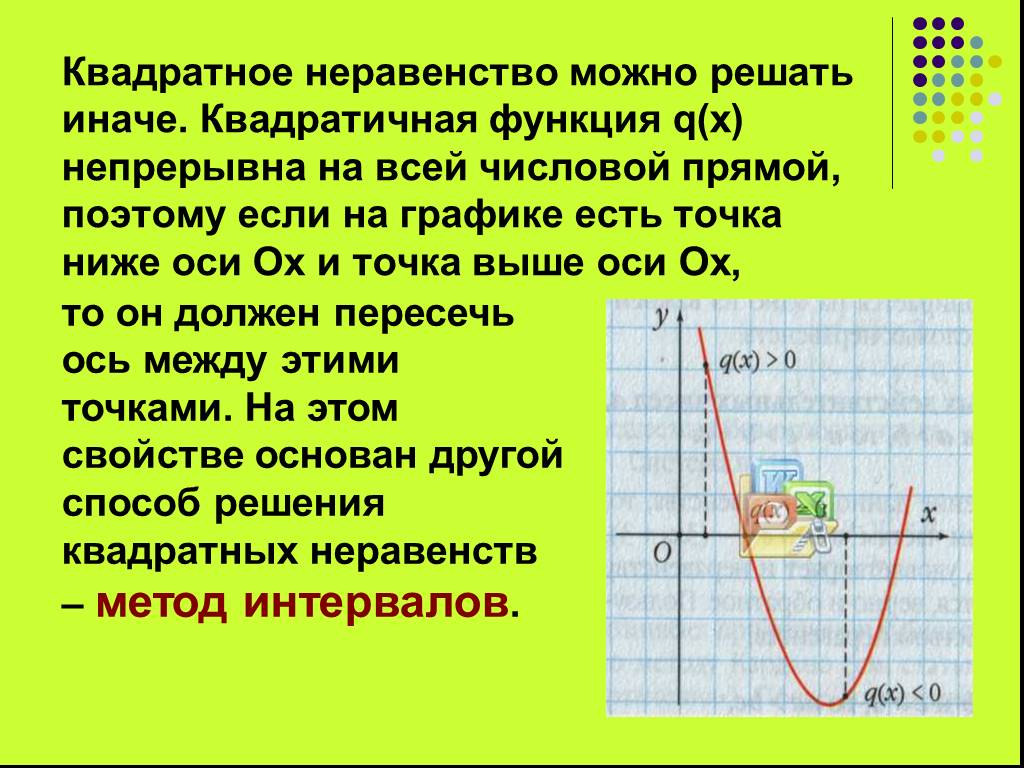
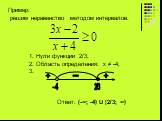
Презентация "Алгоритм решения неравенств" по математике – проект, доклад
Презентацию на тему "Алгоритм решения неравенств" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
решение неравенств первой степени с одной переменной (графический способ решения)
Тема: решение неравенств первой степени с одной переменной (графический способ решения). ах + в > o cх + d. Цели урока: Повторить свойства числовых ...Неравенства и их решения
Неравенство Решить неравенство. Совокупность неравенств. Неравенства Алгебраические Трансцендентные рациональные иррациональные. Пример: Решить неравенство ...Метод интервалов решения неравенств
Решение неравенства. Решением неравенства с неизвестным х называют число, при подстановке которого в это неравенство вместо х получается верное числовое ...Методы решения неравенств с одной переменной
1. Алгебраические методы решения. Если исходить из определения неравенства, в котором в обеих частях записаны выражения с переменной, то при решении ...Блок-схема для решения квадратных неравенств
Неравенства второй степени вида. D. D=0 x=m m. D>0 m n. . . . . . . . Нет решения. . . . . . . . . Тренажер. решение квадратных неравенств. Варианты ...Графический способ решения неравенств
График – говорящая линия, которая может о многом рассказать. М.Б. Балк. №1 №3. Шумит волна, звенит струна, Гитара поёт и поёт. Поёт о той, что вновь ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач
Объект исследования: Теорема Пифагора и пифагоровы тройки. Предмет исследования: Применение пифагоровых троек для быстрого решения геометрических ...Способы решения систем линейных уравнений
Презентация составлена учителем математики МОУ «СОШ» п. Аджером Корткеросского района Респубрики Коми Мишариной Альбиной Геннадьевной. Способы решения:. ...Решение уравнений и неравенств, содержащих модуль
Чем больше я знаю, Тем больше умею.Правильно! Запишите число противоположное данному:.
7 – 7 – 4 4 –(–5) – 5 –(+3) 6 – 2 9 8 +(–6) –(–2) –(+9) ...
Решение простейших тригонометрических неравенств
11.09.2019. На Оу отмечаем значение. и соответствующие точки на окружности. Выделяем нижнюю часть окружности (обход совершаем против часовой стрелки). ...Решение неравенств методом интервалов
0 x y. Пусть графиком функции y=f(x) является некоторая гладкая кривая:. y=f(x). Очевидно, что D(f)=E(f)=. Обратим свое внимание на значения аргумента ...Решение неравенств второй степени с одной переменной
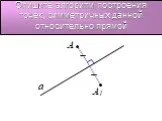
Тема урока « Решение неравенств второй степени с одной переменной». План урока. Повторение по теме «Квадратичная функция и её свойства» Изучение нового ...Алгоритм построения точек, симметричных данной относительно прямой
Постройте точки, симметричные данным относительно прямой. A1 B B1. Существует ли на плоскости точка, для которой нет точки, симметричной ей относительно ...Решение иррациональных неравенств
Содержание. Теория: - определение - свойства - способы решения Задания для решения вместе Задания для самостоятельной работы Задания для работы в ...Аналитический и численный методы решения систем уравнений с параметром
АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...Аналитические методы решения логарифмических уравнений
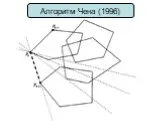
Цели урока:. Обобщить и систематизировать изученные методы решения логарифмических уравнений Выявить особенности каждого метода Выяснить, всегда ли ...Алгоритм Чена (1996)
. 1 Розділимо множину P на n/m непересічних підмножин Pi 2 Побудуємо опуклі оболонки CH (Pi) 3 Знайдемо точку p_start, яка буде гарантовано включена ...Алгоритм с ветвлениями и циклами.
Линейный алгоритм. "Соберись в школу" Начало Конец Встань Умойся Сделай зарядку Оденься Позавтракай Собери портфель. Ветвление. "Раскрась крышу дома". ...Конспекты
Применение метода интервалов для решения неравенств
Применение метода интервалов для решения неравенств. . . 9-й класс. Цель урока:. рассмотреть применение метода интервалов для решения неравенств ...Свойства уравнений и воспроизвести алгоритм решения уравнений, содержащих переменную в обеих частях
Муниципальное казённое общеобразовательное учреждение. «Средняя общеобразовательная школа №1 г.Суздаля». Учитель математики: Плотникова Татьяна ...Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Нестандартные методы решения уравнений и неравенств. Использование области определения функций
Тема урока: Нестандартные методы решения уравнений и неравенств. Использование области определения функций. . ФИО (полностью). . Кривошеин ...Нестандартные способы решения показательных и логарифмических уравнений и неравенств
Тема: Нестандартные способы решения. показательных и логарифмических уравнений. и неравенств.(11 класс). Капацына Людмила Константиновна, СШЛ №23 ...Методы решения уравнений и неравенств
Тема: «Методы решения уравнений и неравенств». 9 класс. ГБОУ СОШ №1968. Учитель математики: Осина И.В. Г.Москва. Тип урока. :. Урок обобщения ...Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции
Конспект урока по алгебре и началам анализа по теме. «Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции». . ...Квадратное неравенство. Графический способ решения
Автор:. Перханова Валентина Кирилловна. Полное название образовательного учреждения. : Иркутская область, Ольхонский район, п. Бугульдейка, МКОУ ...Методы решения показательных и логарифмических уравнений и неравенств
Тема урока: «Методы решения показательных и логарифмических уравнений и неравенств». Тип урока:. . Цели урока: урок обобщения и систематизации ...Уравнение. Понятие корня уравнения. Алгебраический способ решения задач
Конструкт урока по математике. 5 класс. . . Омарова Гульнара Кавыевна. МКОУ «СОШ №13». с. Мариинск. ГО Ревда. Пояснительная ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 мая 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию