Конспект урока «Квадратное неравенство. Графический способ решения» по математике для 9 класса
Автор: Перханова Валентина Кирилловна
Полное название образовательного учреждения: Иркутская область, Ольхонский район, п. Бугульдейка, МКОУ «Бугульдейская СОШ»
Предмет : математика
Класс: 9
Тема урока: Квадратное неравенство. Графический способ решения
Цель урока: исследования свойств квадратичной функции с использованием эскиза графика функции
Задачи урока:
-
Образовательные – усвоение алгоритма построения геометрической модели (эскиза) графика квадратичной функции на основе ее аналитической модели; установление связей между этими моделями для решения квадратных неравенств
-
воспитательные – развитие понятийного мышления; развитие произвольных мыслительных процессов, направленных на решение 4 стадий поставленной задачи:
1. подготовка
2. созревание решения
3.вдохновение
4.проверка найденного решения
Развитие познавательных интересов учащихся через активную поисковую деятельность
-
развивающие – вовлечение учащихся в процесс творческого мышления через индивидуальную самостоятельную деятельность на уроке
Учебно-методическое обеспечение: Алгебра 9 класс: учебник для общеобразовательных учреждений/А45Х [Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова]; под редакцией С.А. Теляковского. – 17 изд. – М.:Просвещение, 2012. – 271 с.
Время реализации урока: 45 мин
Авторский медиапродукт:
1. программа для подготовки презентаций MS PowerPoint, графический редактор Advanced Grapher
2. вид медиапродукта: наглядная презентация
Необходимое оборудование и материалы для урока-занятия: компьютер, видеопроектор, экран, листы формата А4 с подготовленными шаблонами координатной плоскости, цветные фломастеры, демонстрационные таблицы с формулами вычисления дискриминанта и корней квадратного уравнения, таблица квадратов, демонстрационные плакаты с графиками квадратичной функции.
План проведения урока:
| Временная реализация | |
| Организационный | 1 мин. |
| Актуализация знаний | 4 мин |
| Мотивация учебной деятельности | 5 мин |
| Изучение новой темы | 10 мин |
| Закрепление нового материала. | 20 мин |
| Итог урока | 5 мин |
Ход урока:
-
Этап. Организационный. Подготовка класса к уроку, концентрация внимания, дисциплина, собранность.
-
Актуализация знаний. Слово учителя.
Этап проверки домашнего задания – одно из условий обучения, где знания приобретаются в форме повторного открытия. Домашнее задание прошлого урока представлено на слайде 4. 
Метод проверки – самопроверка. На экране учителем будут представлены графики в программе Advanced Grapher.
В фронтальном режиме идет опрос на поставленные вопросы задания. Актуализируем необходимые знания:
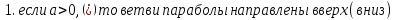
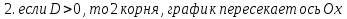
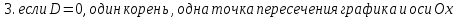
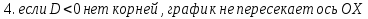
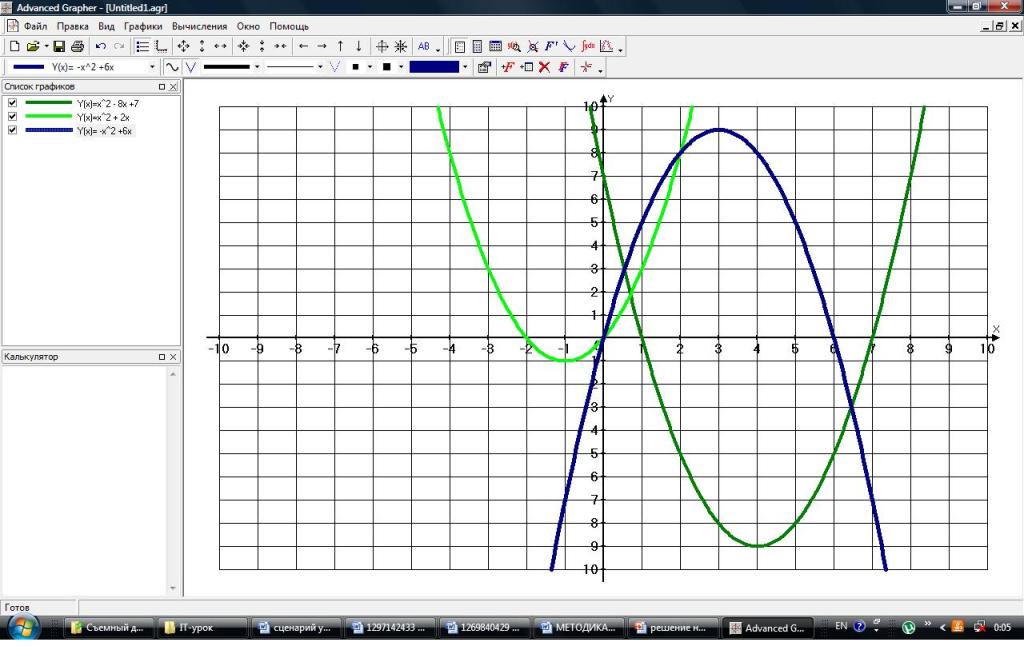
Пример проверки домашнего задания. Слайд 5
-
Этап мотивации учебной деятельности. Сообщение темы урока – слайд 6
Мотивация учебной деятельности: учащимся предлагается ответить на вопросы учителя:
-
Возможно ли, зная знак старшего коэффициента a квадратного трехчлена
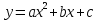 и корней квадратного уравнения
и корней квадратного уравнения 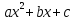 = 0 схематически построить график?
= 0 схематически построить график?
Ответ: да, зная направление ветвей параболы. Направление ветвей зависит от знака старшего коэффициента а.
-
Аналогичны ли записи
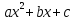 > 0 и y> 0. Ответ: да
> 0 и y> 0. Ответ: да
Вместе с учащимися формулируем вывод: задача о решении неравенства может быть переформулирована в задачу о нахождении промежутков,( т.е значений переменной х) на которых функция ( т.е. значения переменной у) принимает либо отрицательные значения, либо положительные, т.е. исследуем функцию.
-
Обязательно ли вычислять координаты вершины параболы при решении неравенства? Вместе с учащимися формулируем вывод: для построения эскиза графика функции достаточно построить ось симметрии параболы и на ней отметить координату вершины в зависимости от направления ветвей.
Учитель обобщает все выводы в один общий: нужно установить связь между геометрической моделью и аналитической моделью квадратичной функции .Для этого необходимо провести исследование свойств графика.
В тетради записывается алгоритм построения эскиза графика функции для решения неравенств:
-
Найти корни уравнения в зависимости от значения дискриминанта
-
Определить направление ветвей параболы в зависимости от знака коэффициента а.
-
Построить ось симметрии параболы. Отметить на ней примерно координату вершины параболы, зная направление ветвей.
-
Провести параболу через данные точки
-
Определить промежутки, на которых функция отрицательна или положительна (y>0 или y
-
Формируем понятие квадратного неравенства.
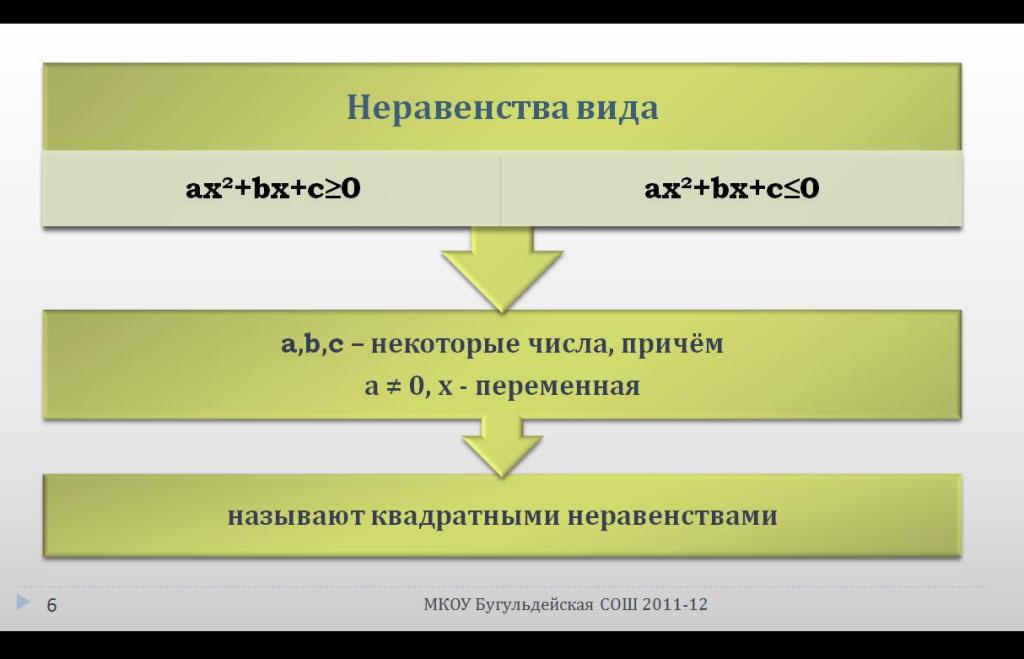
Слайд 7
-
Этап. Закрепление материала.
Слайд 8, 9, 10. Разбираем пример, когда D>0. Проговариваем все пункты построения, учащиеся строят график на готовых шаблонах координатной плоскости. Учитель одновременно показывает в программе Advanced Grapher все этапы построения.
Слайд 11, 12. Разбираем пример, когда D=0. Оформляем решение на готовых шаблонах.
Слайд 13, 14. Разбираем случай, когда DОформляем решение на готовых шаблонах.
Слайд 15. Обобщаем и систематизируем изученный материал.
Слайд 17,18,19,20,21. Самостоятельная исследовательская работа. На базе приобретенных в ходе исследования свойств квадратичной функции знаний, усложняем задание – активизируем мыслительные процессы. Задание от обратного: зная промежутки значений переменной х определить знак неравенства. Работу выполняют на готовых шаблонах. Проверку осуществляет учитель в программе Advanced Grapher. На экране учащиеся сверяют ответы и оценивают задание:
+ верно выполнено
- не верно выполнено
Подсчитывается количество баллов. Все задания верно выполнены – 4 балла.
-
Рефлексия. Слайд 23,24 Устное задание. Подведение итога урока. Оценивание по количеству набранных баллов. Домашнее задание.
Здесь представлен конспект к уроку на тему «Квадратное неравенство. Графический способ решения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

