Конспект урока «Графический способ решения уравнений в среде Microsoft Excel 2007» по математике

Графический способ решения уравнений в среде Microsoft Excel 2007

Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.

Цели и задачи урока:

• повторение изученных графиков функций;

• повторение и закрепление графического способа решения уравнений;

• закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;

• формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;

• формирование мышления, направленного на выбор оптимального решения;

• формирование информационной культуры школьников.

Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.

Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).

Ход урока

Организационный момент.

Слайды 1-3 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).

Объявление темы урока.

1. Устная работа (актуализация знаний).

Слайд 4 - Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):

у = 6 - х; у = 2х + 3; у = (х + 3)²; у = -(х - 4)²; .

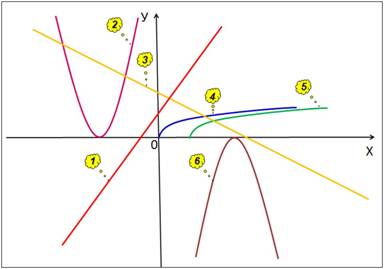
Рис. 1.

Слайд 5 Графический способ решения уравнений вида f(x)=0.

Корнями уравнения f(x)=0 являются значения х₁, х₂, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).

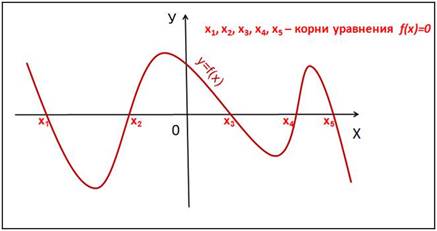
Рис. 2.

Слайд 6

Найдите корни уравнения х²-2х-3=0, используя графический способ решения уравнений (Рис.3).

Ответ: -1; 3.

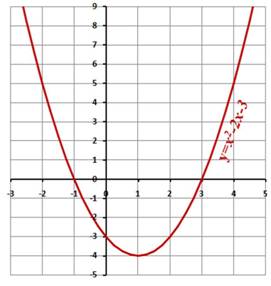
Рис. 3.

Слайд 7 Графический способ решения уравнений вида f (x)=g (x).

Корнями уравнения f(x)=g(x) являются значения х₁, х₂, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):

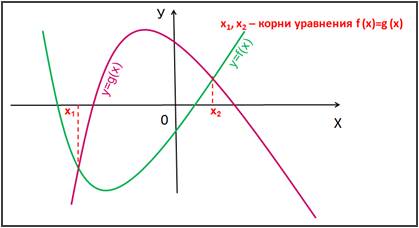
Рис. 4.

Слайд 8 Найдите корни уравнения , используя графический способ решения уравнений (Рис. 5).

Ответ: 4.

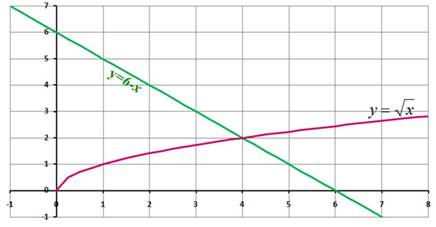
Рис. 5.

2. Объяснение нового материала. Практическая работа.

Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).

I. Графический способ решения уравнений вида f(x)=0 в Excel.

Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.

Слайд 9

Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение -х²+5х-4=0.

Для этого: построить график функции у=-х²+5х-4 на промежутке [ 0; 5 ] с шагом 0,25; \найти значения х точек пересечения графика функции с осью абсцисс.

Выполнение задания можно разбить на этапы:

1 этап: Представление функции в табличной форме (рис. 6):

Рис. 6.

Для этого:

• в ячейку А1 ввести текст Х, в ячейку A2 — Y;

• в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;

• выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).

Рис. 7.

• в ячейку B2 ввести формулу =-(B1^2)+5*B1-4;

При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.

После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул - сама формула (Рис. 8):

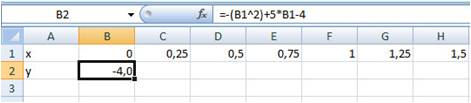
Рис. 8.

• скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.

2 этап: Построение диаграммы типа График.

Для этого:

• выделить диапазон ячеек B2:V2;

• на вкладке Вставка|Диаграммы|График выбрать вид График;

• на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси - откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;

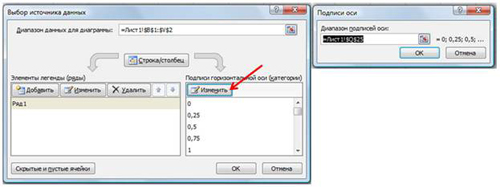
Рис. 9.

• на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:

Интервал между делениями: 4;

Интервал между подписями: Единица измерения интервала: 4;

Положение оси: по делениям;

Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);

• самостоятельно изменить ширину и цвет линии для вертикальной оси;

• на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.

Примерный результат работы приведен на рис. 10:

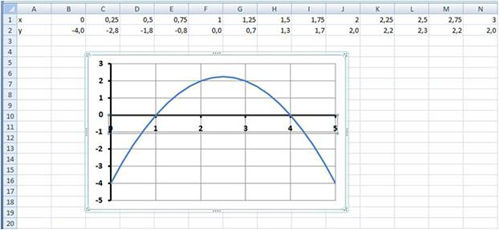
Рис. 10.

3 этап: Определение корней уравнения.

График функции у=-х²+5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х²+5х-4=0 имеет два корня: х₁=1; х₂=4.

II. Графический способ решения уравнений вида f(x)=g(x) в Excel.

Слайд 10

Пример 2: Решить графическим способом уравнение .

Для этого: в одной системе координат построить графики функций у₁= и у₂=1-х на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки пересечения графиков функций.

1 этап: Представление функций в табличной форме (рис. 1):

• Перейти на Лист2.

• Аналогично Примеру 1, применив приемы копирования, заполнить таблицу. При табулировании функции у₁= 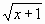воспользоваться встроенной функцией Корень (Рис. 11).

Рис. 11.

2 этап: Построение диаграммы типа График.

• Выделить диапазон ячеек (А2:V3);

• Аналогично Примеру 1 вставить и отформатировать диаграмму типа График, выбрав дополнительно в настройках горизонтальной оси: вертикальная ось пересекает в категории с номером 5.

Примерный результат работы приведен на Рис. 12:

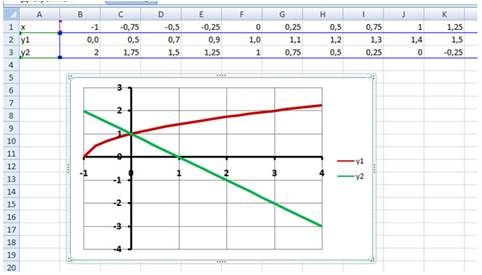
Рис. 12.

3 этап: Определение корней уравнения.

Графики функций у₁= и у₂=1-х пересекаются в одной точке (0;1) и, следовательно, уравнение имеет один корень – абсцисса этой точки: х=0.

III. Метод Подбор параметра.

Слайд 12

Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.

Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.

Слайд 13

Пример 3: Разберем метод Подбор параметра на примере решения уравнения -х²+5х-3=0.

1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.

Построить график функции у=-х²+5х-3, отредактировав полученные в Примере 1 формулы.

Для этого:

• выполнить двойной щелчок по ячейке B2, внести необходимые изменения;

• с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.

Все изменения сразу отобразятся на графике.

Примерный результат работы приведен на Рис. 13:

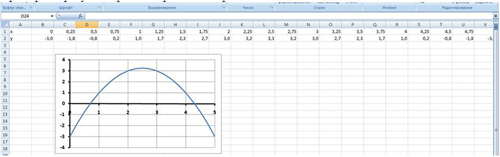
Рис. 13.

2 этап: Определение приближенных значений корней уравнения.

График функции у=-х²+5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х²+5х-4=0 имеет два корня.

По графику приближенно можно определить, что х₁≈0,7; х₂≈4,3.

3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.

1) Начать с поиска более точного значения меньшего корня.

По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.

• Выделить ячейку Е2;

• перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;

В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.

В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).

Щелкнуть по кнопке ОК.

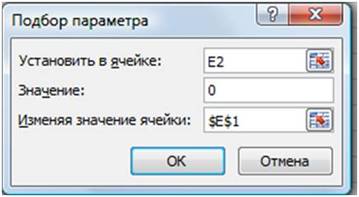
Рис. 14.

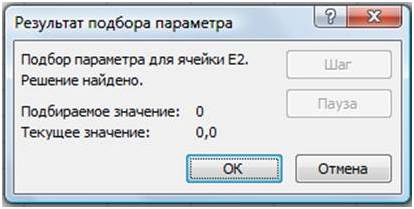
Рис. 15.

• В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:

• В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).

Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).

Итак, первый корень уравнения определен с заданной точностью: х₁≈0,6972.

2) Самостоятельно найти значение большего корня с той же точностью. (х₂≈4,3029).

IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).

При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.

3. Закрепление изученного материала. Самостоятельная работа.

Слайд 14

Задание: Используя метода Подбор параметров, найти корни уравнения с точностью до 0,001.

Для этого:

• ввести функцию у= 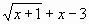и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):

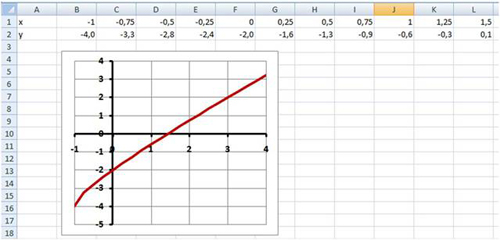
Рис. 16.

• найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);

• найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).

4. Итог урока.

Слайд 15 Проверка результатов самостоятельной работы.

Слайд 16 Повторение графического способа решения уравнения вида f(x)=0.

Слайд 17Повторение графического способа решения уравнения вида f(x)=g(x).

Выставление оценок.

5. Домашнее задание.

Слайд 18 .

Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х²-5х+2=0 с точностью до 0,01.

6. Рефлексия.

Слайд 19.