Конспект урока «Общие методы решения уравнений» по математике

Конспект занятия по теме «Общие методы решения уравнений»

2 урока по 45 минут

Цели урока

Обучающие: обобщить ранее накопленные теоретические знания по теме «Общие методы решения уравнений»;

развивающие: развивать у учащихся умения анализировать задачу перед выбором способа ее решения; развивать навыки исследовательской деятельности, синтеза, обобщения; учить сопоставлять условия;

воспитывающие: предоставить учащимся возможность осознать значимость себя, почувствовать уверенность в своих силах.

На уроке используются: компьютер, интерактивная доска Smart Board.

I этап урока – организационный (1 минута)

Учителем сообщается тема урока и цели урока.

II этап урока (10 минут)

Актуализация знаний: повторяются методы решения показательных, логарифмических, иррациональных уравнений; теоремы о равносильных уравнениях ( на доске вывешивается плакат: теоремы о равносильности уравнений).

Ш этап урока

Общие методы решения уравнений.

1. Замена уравнения h(f(x)) = h(g(x)) уравнением f(x) = g(x) (слайд № 2)

Этот метод используется

а) при решении показательных уравнений переходим от

уравнений а^f(x) = a^g(x) (a>0, а=1) к уравнению f(x) = g(x)

С помощью интерактивной доске рассматривается решение уравнения (решает один ученик на доске)

2^{5х – 7} = 2³.

б) при решении логарифмических уравнений переходим от уравнения log_af(x) = log_ag(x) (a>0, а=1) к уравнению f(x) = g(x) ( f(x)>0, g(x) >0)

С помощью интерактивной доске рассматривается решение уравнения (решает один ученик на доске)

log ₇ (x + 6) = log ₇ (x² - 5x -10)

в) при решении иррациональных уравнений переходим от уравнения √f(x) = √g(x) к уравнению f(x) = g(x)

С помощью интерактивной доске рассматривается решение уравнения (решает один ученик на доске)

Этот метод можно применять только в случае монотонности функции h(x), т.к. иначе возможна потеря корня

Пример. (2х+2)² = (5х-9)²

2х + 2 = 5х - 9

х = 11/3

х = 1 - корень уравнения

Весь класс решает вместе с доской номера из учебника (показательное, логарифмическое и иррациональное уравнения).

№1682(а), 1683(б), 1712 (б)

2. Метод разложения на множители (слайд № 3)

Прежде чем переходить к этому методу, следует вспомнить способы разложения на множители: вынесение за скобки общего множителя, способ группировки, с помощью формул сокращенного умножения.

Учитель показывает использование этого способа на интерактивной доске на примере № 1692 (а):

2^х ∙ 4х – 4 + 2^х = 0.

Все вместе с доской решают номера из учебника

№ 1690 (б), 1693 (а).

3. Метод введения новой переменной (слайд № 4)

Учитель показывает применение этого метода на примере № 1697 (а):

Для закрепления выполняются номера № 1699 (б), 1690 (в,г)

4. Функционально-графический метод.

а) для начала рассматривается графический метод (слайд № 5)

Идея этого метода решения уравнения f (x) = g(x), очень проста: нужно построить графики уравнений y = f (x) и y = g(x) и найти абсциссы точки(точек) их пересечения (если такие существуют).

Учитель рассматривает на интерактивной доске решение уравнения

б) использование свойств функций

построение графиков можно заменить ссылкой на какие-либо свойства функций. Например:

- если одна функция y = f (x) возрастает, а другая y = g(x) – убывает, то уравнение f (x) = g(x) либо не имеет корней либо имеет один корень (который можно найти подбором) ;

- если на промежутке Х наибольшее значение одной из функций y = f (x),

y = g(x) равно А и наименьшее значение другой функции тоже равно

А, то уравнение f (x) = g(x) равносильно на промежутке Х системе

уравнений: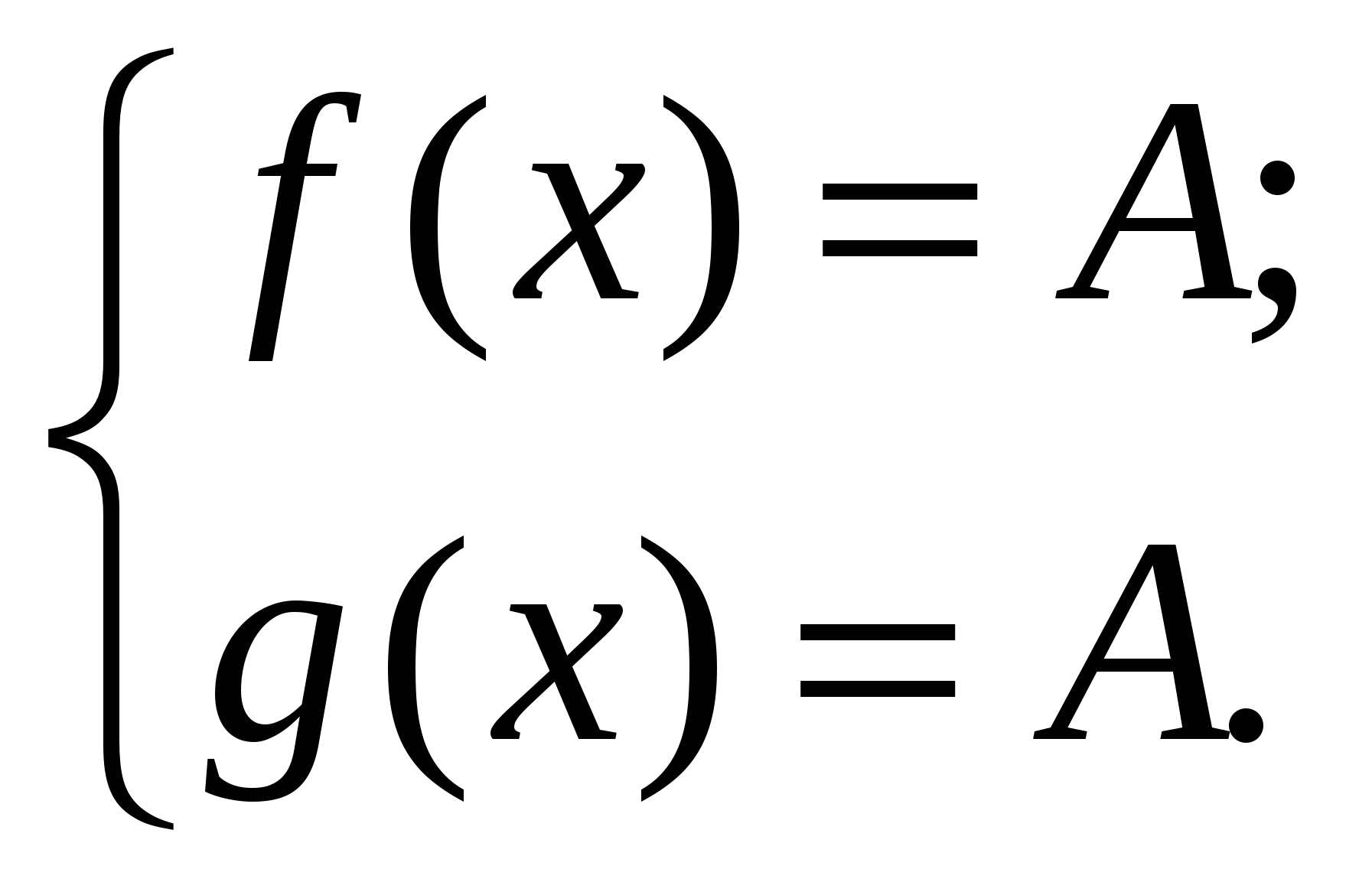

Учитель рассматривает выполнение № 1741 (а) (слайд № 6) и

Решение уравнения (слайд № 7)

IV этап - подведение итогов

Обобщаются методы решения уравнений (слайд 8).

Учитель еще раз обращает внимание, на те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. Отмечает наиболее успешную работу на уроке отдельных учащихся, при необходимости выставляет отметки.

Домашнее задание: по учебнику А.Г. Мордковича

№№ 1682 (б), 1687 (а), 1694 (б), 1703 (а), 1741 (а)