Конспект урока «Способы решения систем двух уравнений с двумя неизвестными» по математике для 7 класса

Открытый урок в 7 классе

Тема урока: «Способы решения систем двух уравнений с двумя неизвестными»

Девиз урока: «Учиться нелёгко, но интересно».

Цели урока:

1. Обобщить знания, умения и навыки учащихся по способам решения систем двух линейных уравнений с двумя переменными и применять эти знания при решении текстовых задач.

2. Развивать логическое мышление учащихся.

3. Вырабатывать умение сравнивать, делать выводы, делать самопроверку.

Оборудование: презентация, экран, мультимедиа.

1. Организационный момент.

Постановка цели урока. Создание условий для успешной совместной деятельности.

- Здравствуйте, ребята! Тема нашего урока: «Способы решения систем двух уравнений с двумя неизвестными». Мы сегодня на уроке продолжим решать системы различными способами. У вас будет возможность проверить себя, как вы умеете применять эти способы при выполнении различных заданий.

2. Проверка домашнего задания.

А сейчас проверим как вы выполнили «Домашнее задание». Поменяйтесь пожалуйста тетрадями с соседом по парте и проверьте решение друг у друга.

№658 ( 2 балла) (Слайд №3)

х га в день – бороновал первый тракторист.

у га в день бороновал второй тракторист.

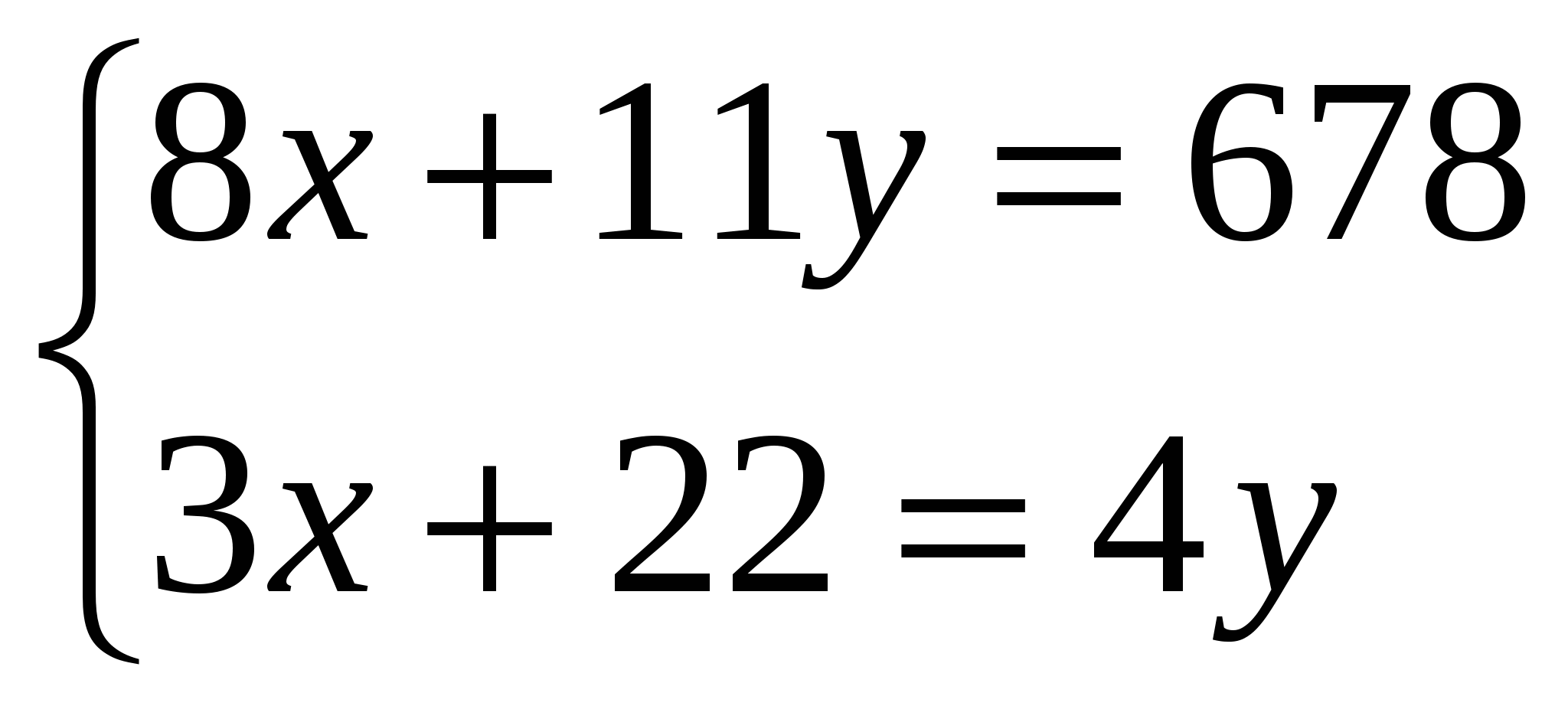
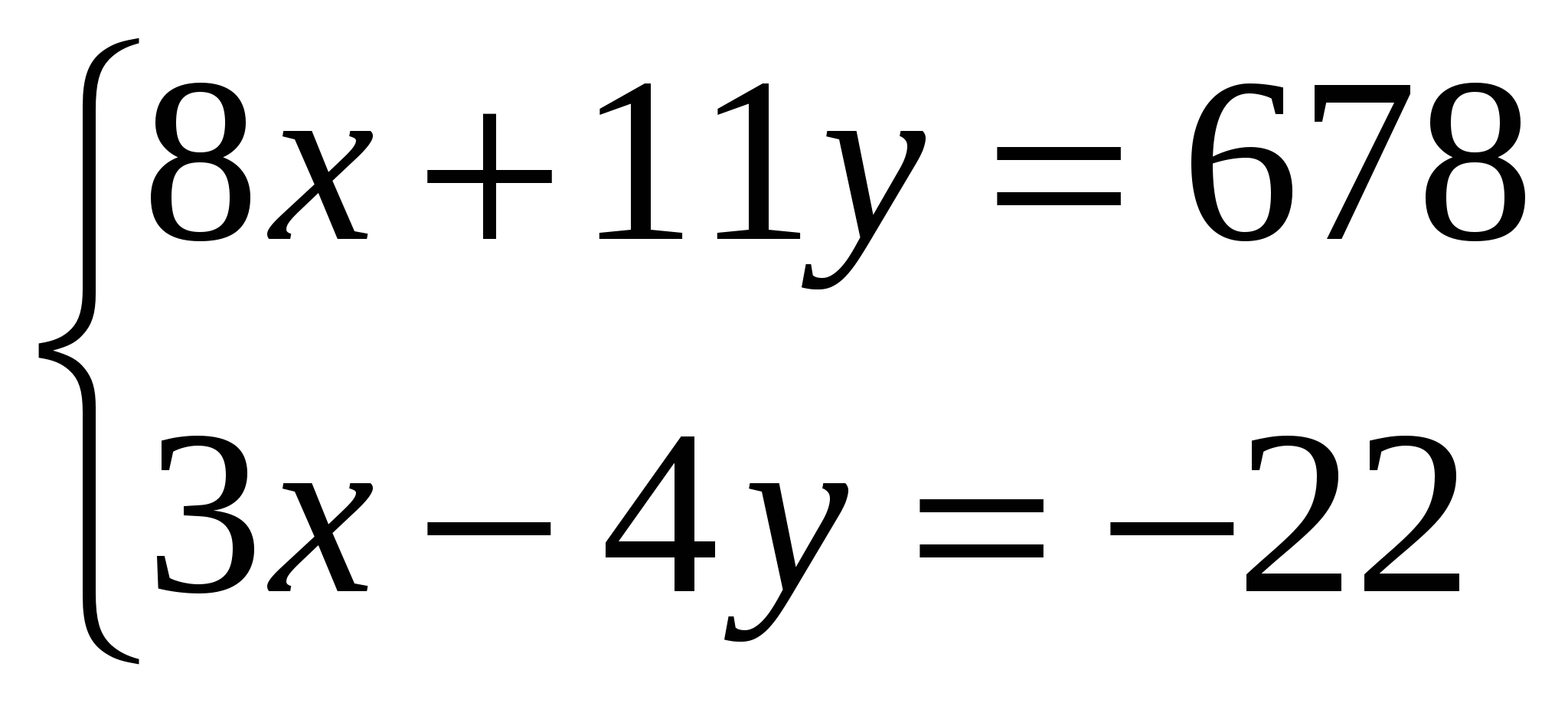
=-65; _х=-2470; _у=-2210; х= = 38; у = = 34

Ответ: 38 га в день бороновал первый тракторист

34 га в день бороновал второй тракторист

№666 ( 2 балла) (Слайд №4)

х деталей – изготовил в январе первый цех

у деталей – изготовил в январе второй цех

1,15х деталей – изготовил в феврале первый цех

1,12у деталей – изготовил в феврале второй цех

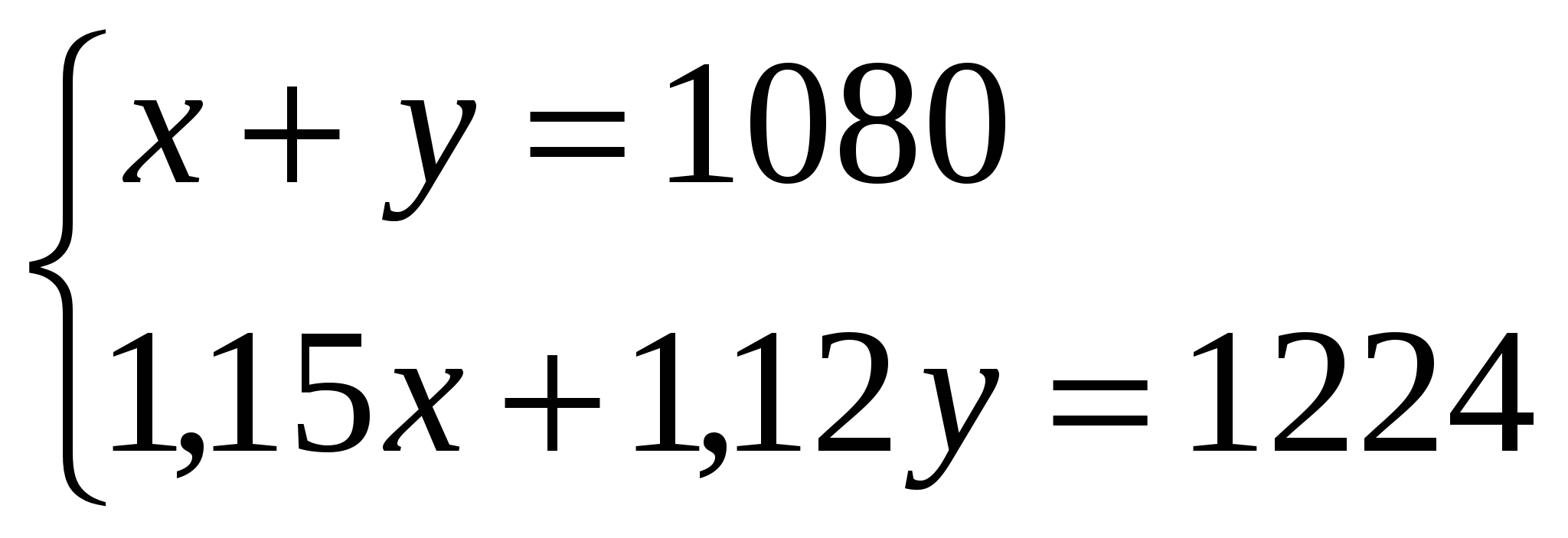
х = 1080 –у; 1,15 (1080 – у) + 1,12у = 1224; 1242 – 1,15у + 1,12у = 1224;

- 0,03у = - 18; у = 600; х = 1080 – 600; х = 480

480 ⋅ 1,15 = 552 детали – изготовил в феврале первый цех

600 ⋅ 1,12 = 672 детали – изготовил в феврале второй цех.

Ответ: 552 детали, 672 детали.

III. Обобщение и систематизация знаний.

2.1 Устные упражнения. (правильный ответ – 1балл)

-Мы с вами в течение нескольких уроков решали системы уравнений различными способами.

-Прежде всего давайте вспомним, что называется решением системы уравнений с 2-мя переменными?

( Решением системных уравнений с двумя переменными называется такая пара чисел х и у, которая при подстановке в эту систему обращает каждое ее уравнение в верное равенство)

-А что значит решить систему уравнений?

( Решить систему уравнений- значит найти все её решения или установить , что решений нет) .

-Какие способы решения систем вы знаете?

( Способ подстановки, способ сложения, способ определителей, графический способ решения систем уравнений).

1. Составьте задачу используя систему уравнений: (Слайд №5)

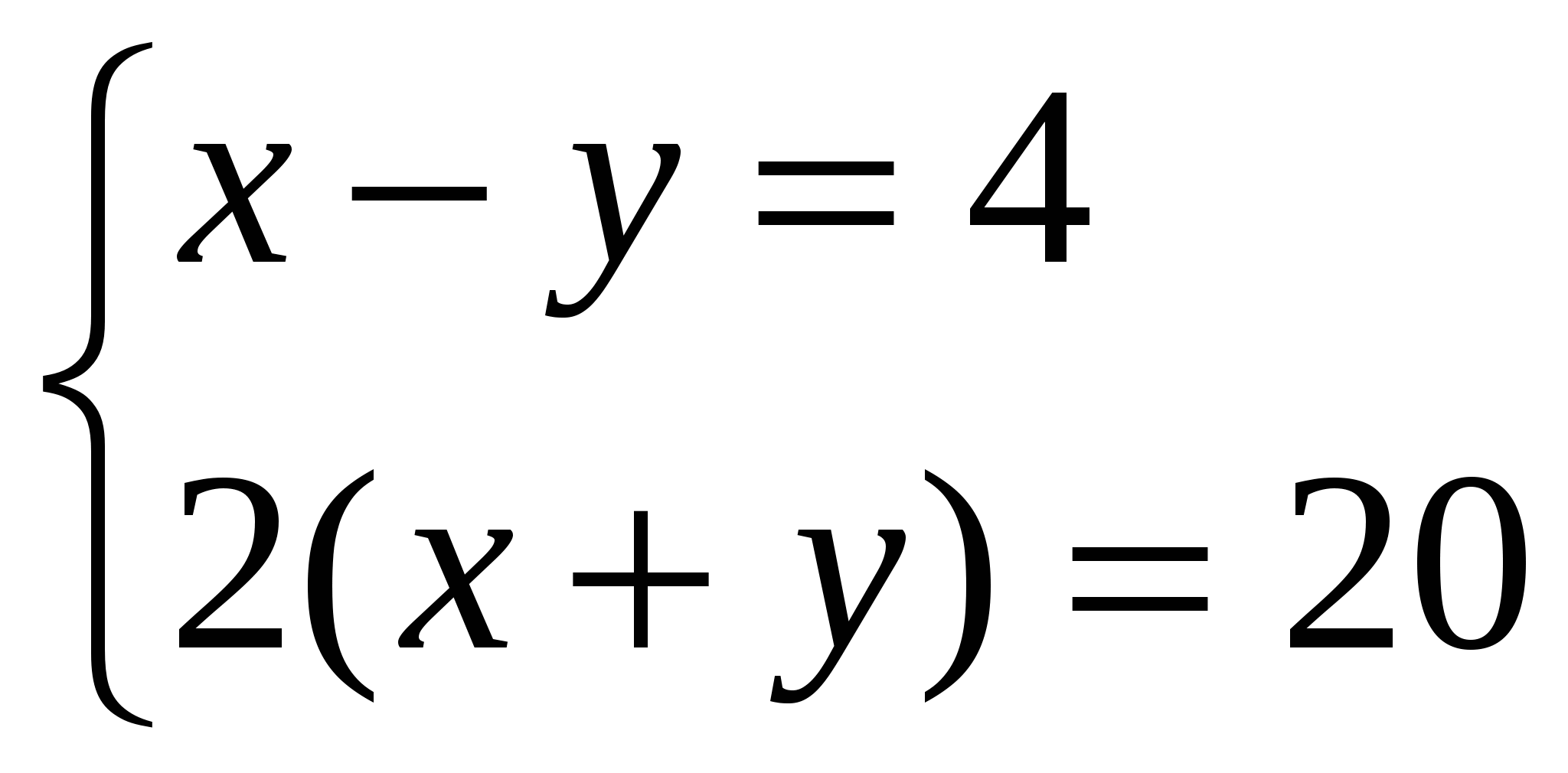
2. Даны три системы уравнений: (Слайд №6)

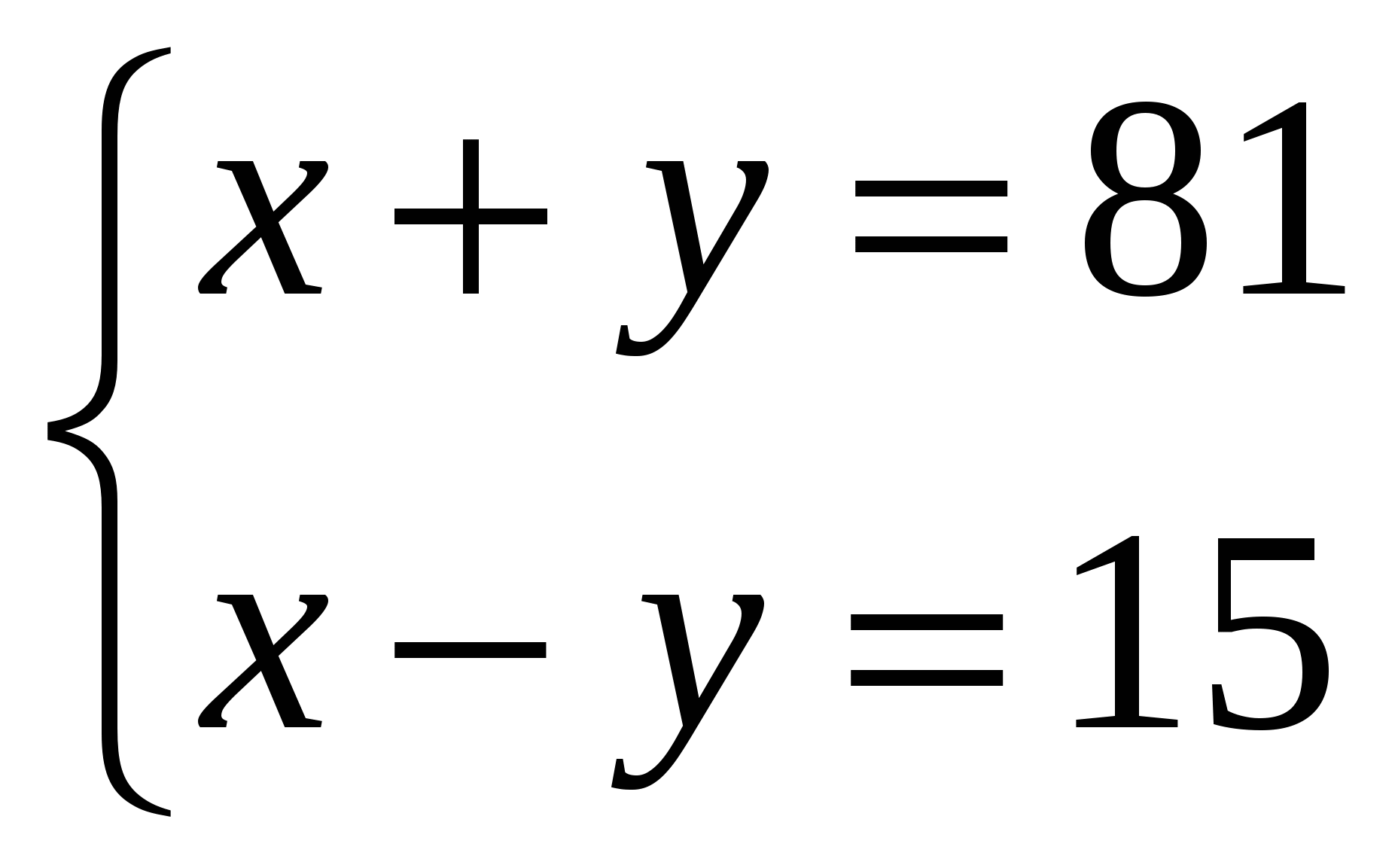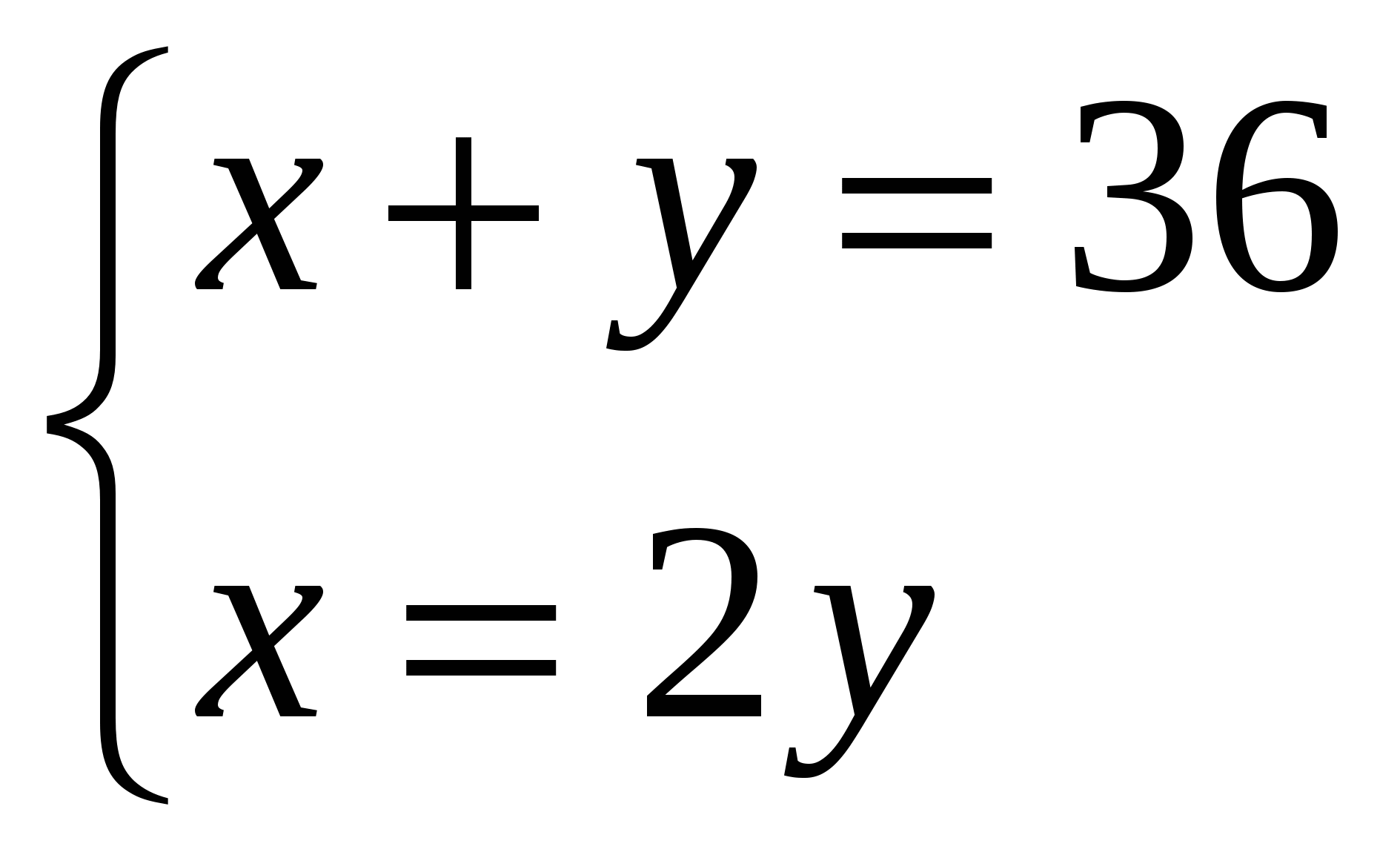а) б) в)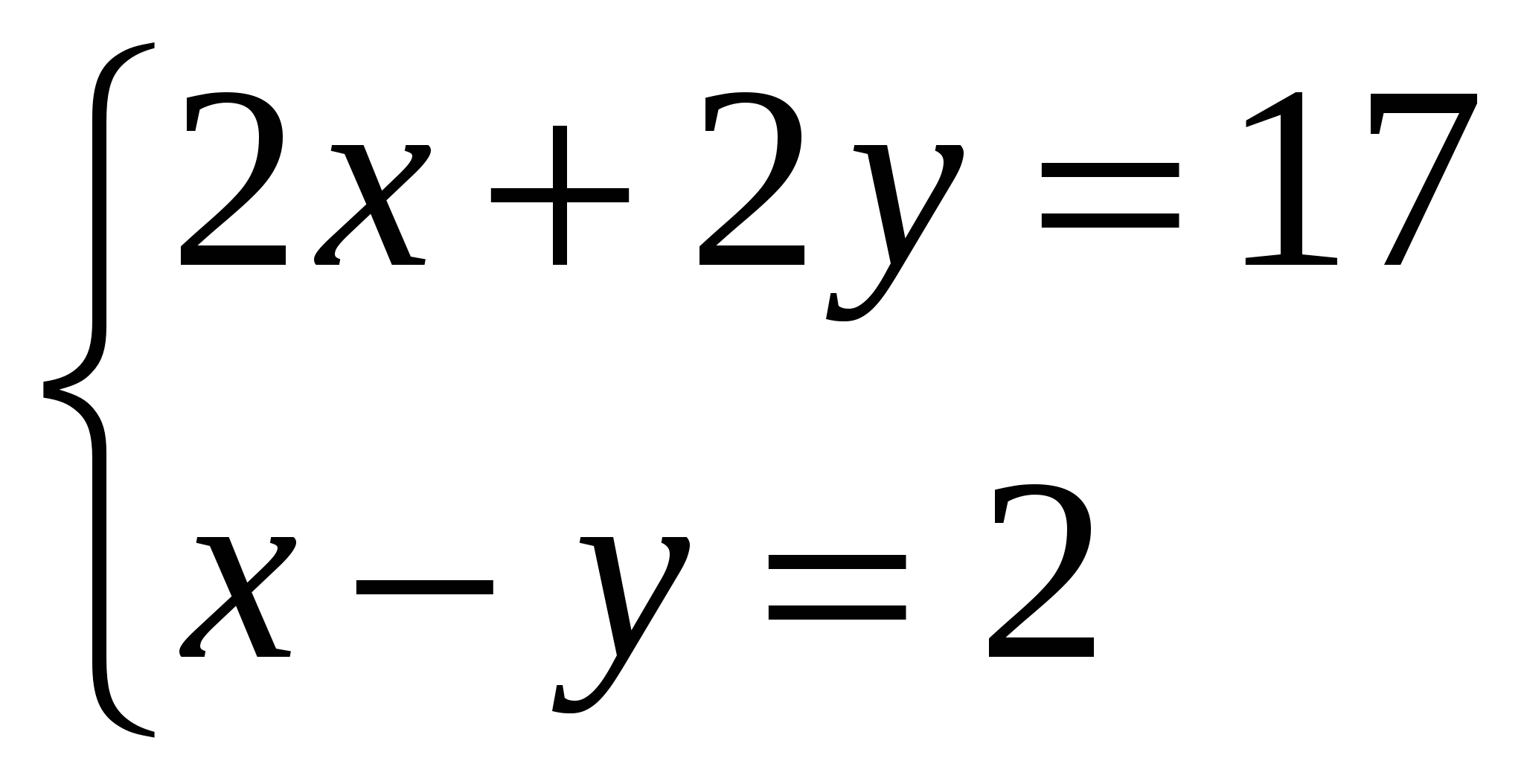

Определите, какая из систем уравнений является решением данной задачи:

1) Сумма двух чисел равна 36. Одно из них в два раза больше другого.

2) Периметр прямоугольника равен 17. Одна из сторон больше другой на 2 см.

3) Сумма двух чисел равна 81, а их разность равна 15.

2.1.3. Сколько решений имеет система? (Слайд №7)

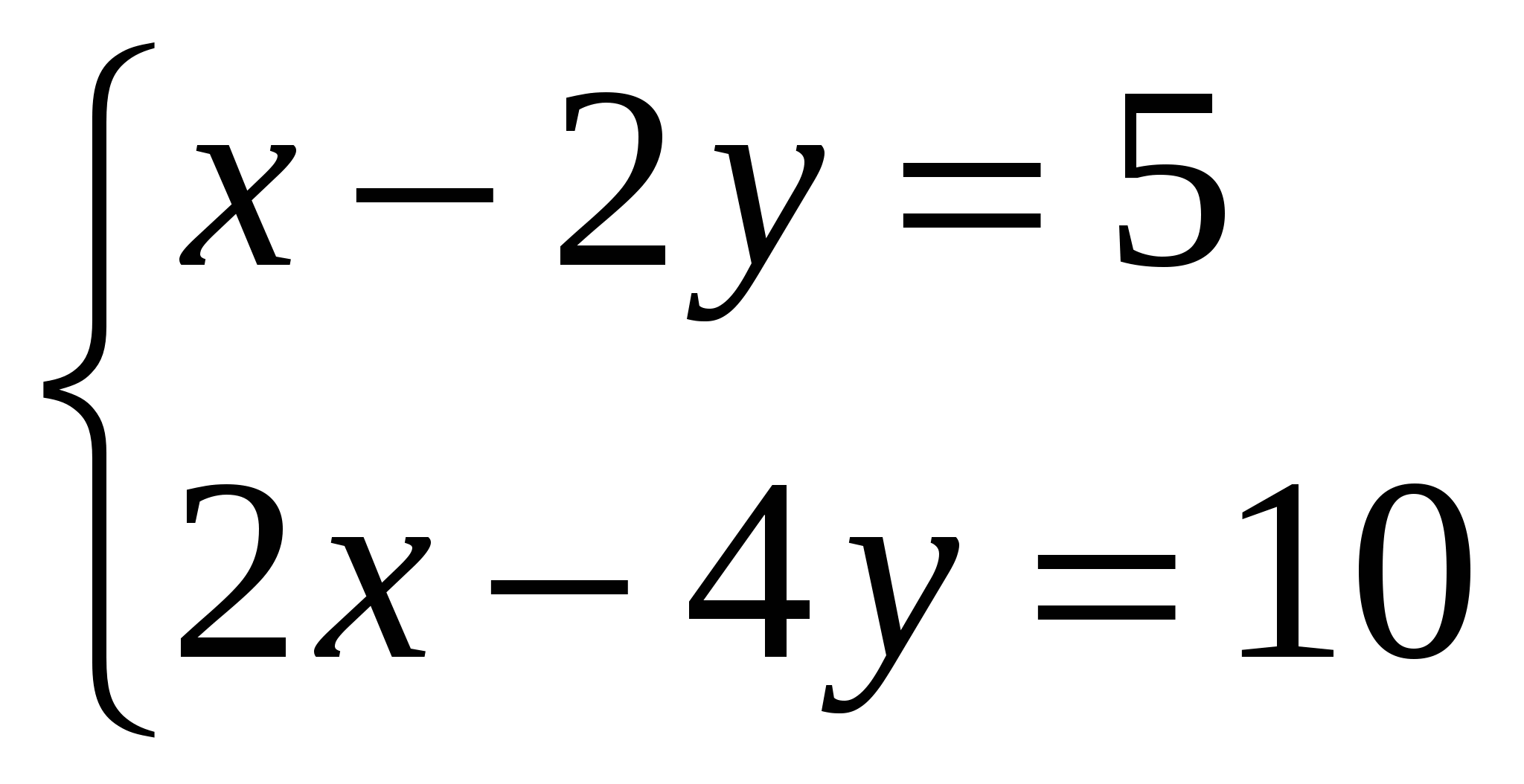
4. Дана система

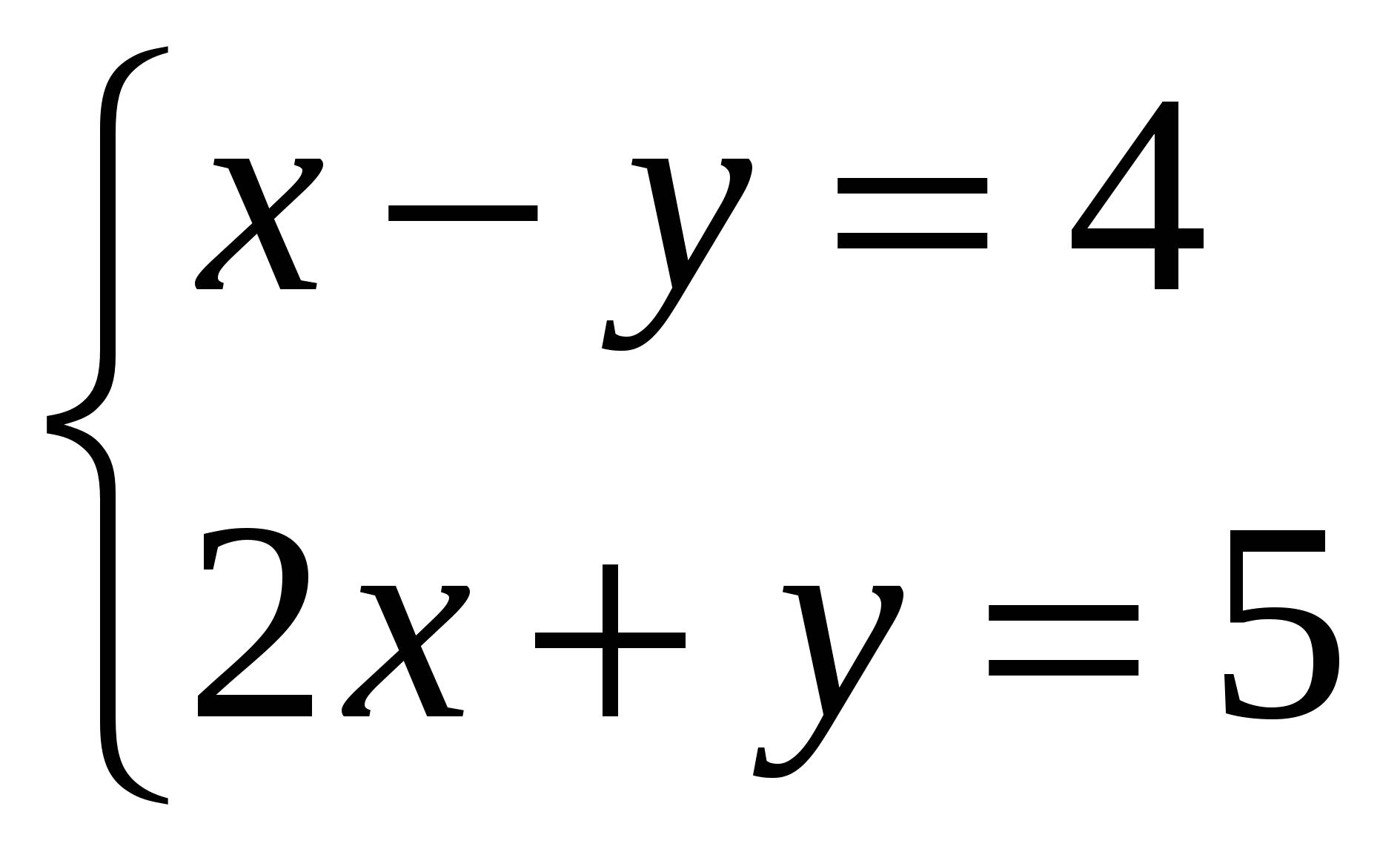
Какая пара чисел является ее решением? (Слайд №8)

а) (4;0) б) (3;0) в) (3; -1)

2.2 Решение задач. (работа в парах)

2.2.1. Сформулируйте алгоритм решения системы уравнений с двумя неизвестными способом подстановки.

1) из одного уравнения системы (все равно из какого) выразить одно неизвестное через другое, например у через х;

2) полученное выражение подставить в другое уравнение системы, получится одно уравнение с одним неизвестным х;

3) решив это уравнение, найти значение х;

4) подставив найденное значение х в выражение для у, найти значение у.

№671(1) . С подробным объяснением у доски Андрей Защеринский.

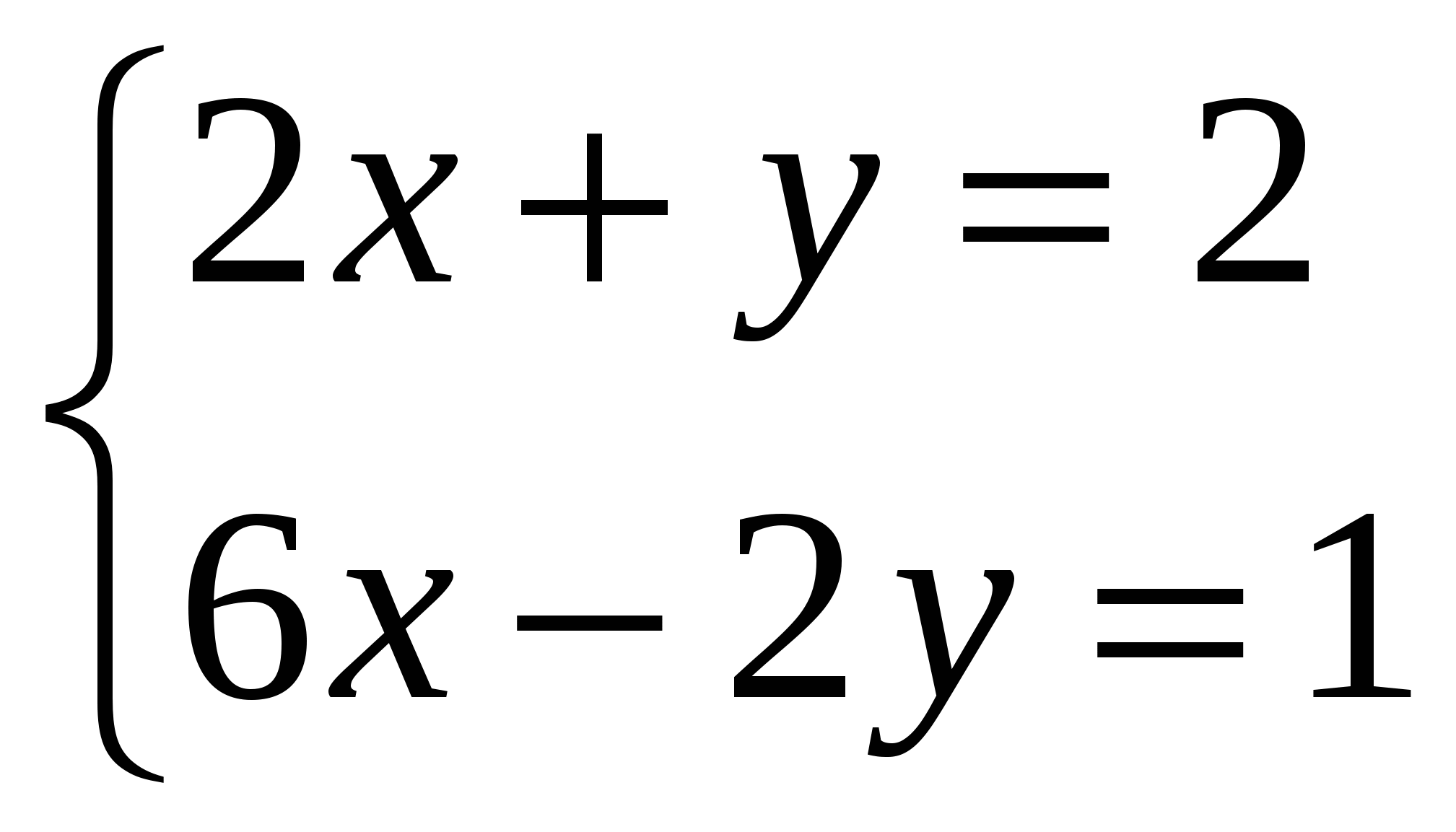у=2 –2х

6х–2(2–2х) =1; 6х-4+4х=1;

10х=5; х=0,5;

у=2-2⋅ 0,5=2-1=1

Ответ: (0,5; 1)

№671(3) – самостоятельно, взаимопроверка. (2 балла) (Слайд №9)

2.2.2. Сформулируйте алгоритм решения систем линейных уравнений с двумя неизвестными способом алгебраического сложения.

Для решения систем линейных уравнений способом алгебраического сложения нужно:

1. Уравнять модули коэффициентов при одном из неизвестных.

2. Складывая или вычитая полученные уравнения, найти одно неизвестное.

3. Подставляя найденное значение в одно из уравнений исходной системы, найти второе неизвестное.

№672(1) Начало решения с подробным объяснением у доски Ваня Соловьев, далее самостоятельно.

Проверка правильности решения. ( 2 балла). (Слайд №10)

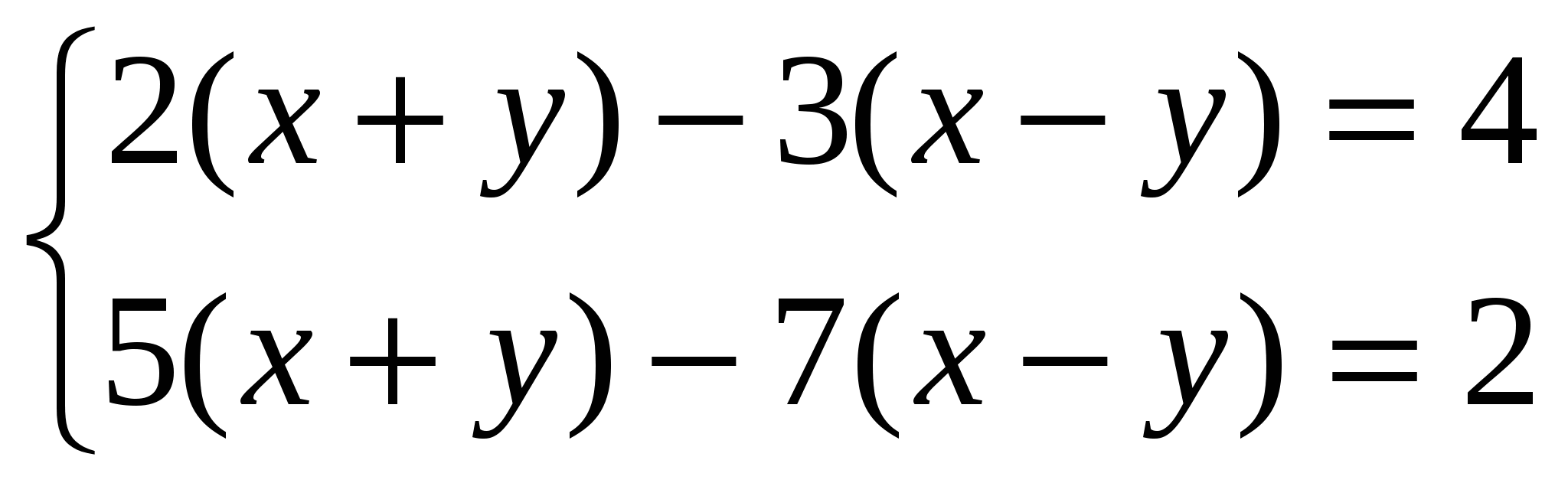
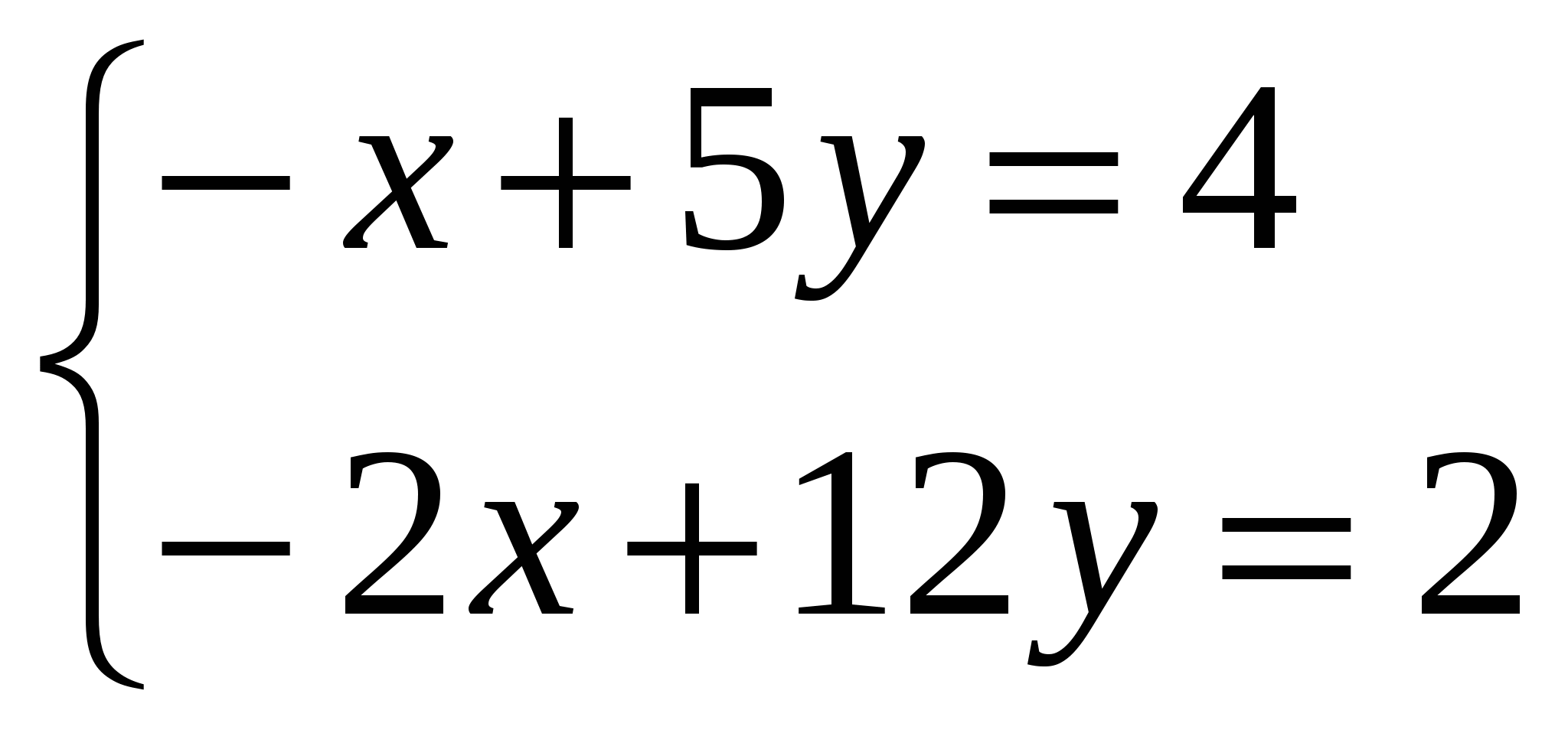
умножаем на (-2)

далее самостоятельно

(+)

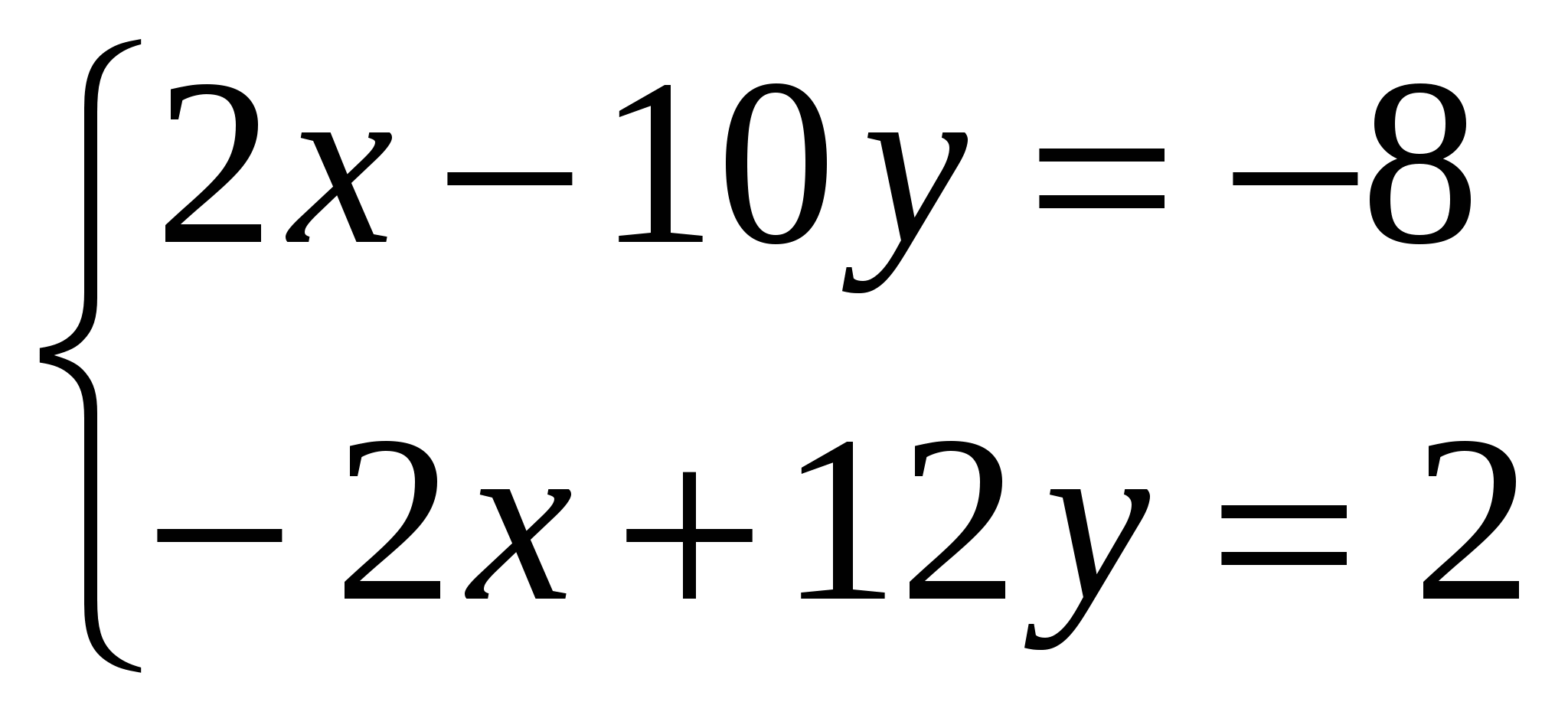2у=-6; у=-3; -х+5(-3)=4; -х-15=4; -х=19; х=-19

Ответ: (-19; -3)

2.2.3. А сейчас давайте вспомним алгоритм решения задач с помощью систем уравнений.

1. Вводят обозначения неизвестных и составляют систему уравнений;

2. Решают систему уравнений;

3. Возвращаясь к условиям задачи и использованным обозначениям записывают ответ.

№677начало задачи комментирует с места Алеша Давыдьян.

х рублей – стоит 1 кг груш первого сорта

у рублей – стоит один кг груш второго сорта

8х руб – стоят 8 кг груш первого сорта

20у руб – стоят 20 кг груш второго сорта

Уравнение: 8х + 20у = 64

5х руб – стоят 5 кг груш первого сорта

7у руб – стоят 7 кг груш второго сорта

Уравнение: 5х – 7у = 1

Составим систему:

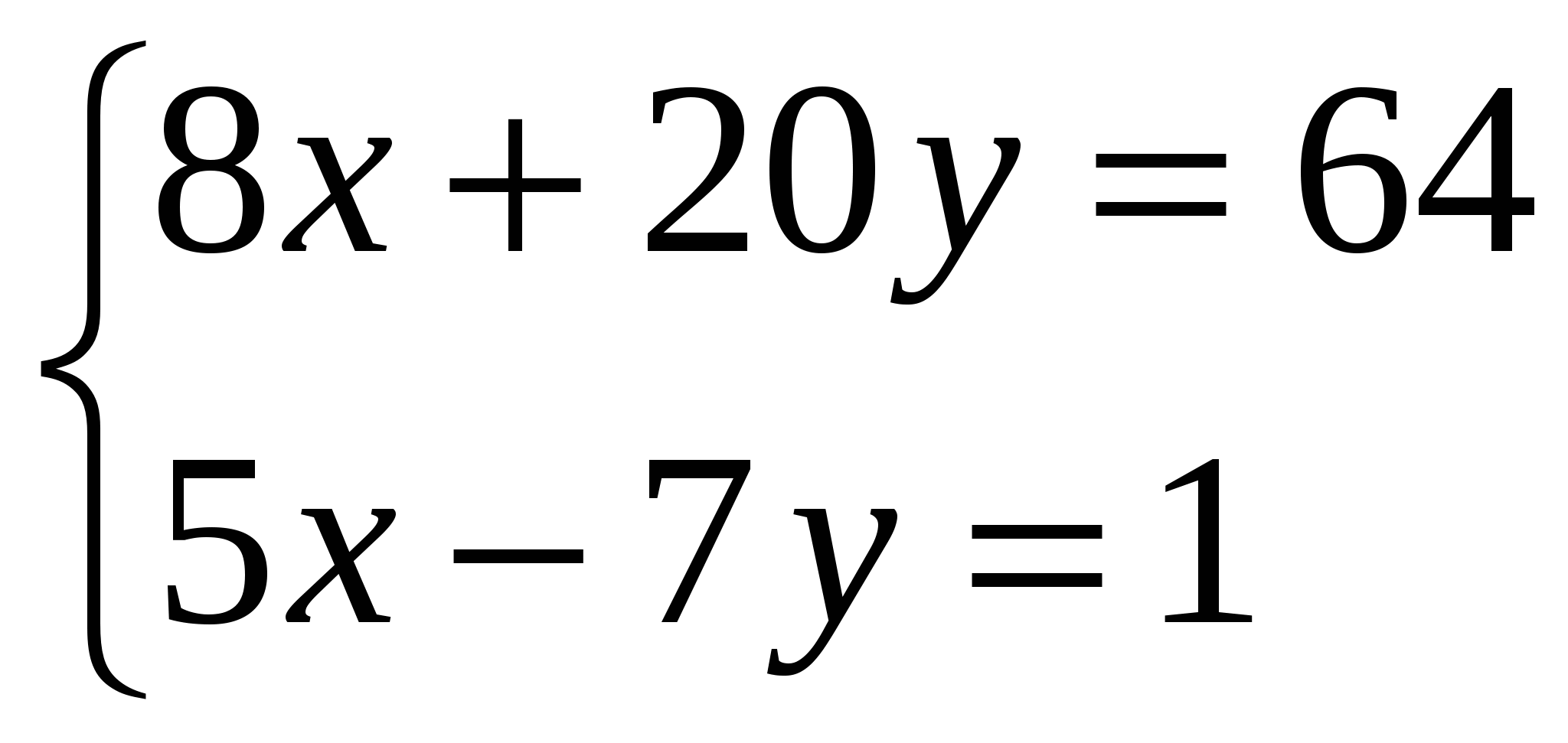
Вспомните пожалуйста алгоритм решения системы способом определителей.

• Составить табличку (матрицу) коэффициентов при неизвестных и вычислить определитель .

• Найти определитель _х, получаемый из заменой первого столбца на столбец свободных членов.

• Найти определитель _у, получаемый из заменой второго столбца на столбец свободных членов.

• Найти значение переменной х по формуле

х =

• Найти значение переменной у по формуле

у =

• Записать ответ.

Решите данную систему самостоятельно способом определителей.

Проверьте правильно ли вы решили ( 2 балла). (Слайд №11)

2.2.4. Наташа Хоряхова приготовила небольшое сообщение «Из истории возникновения уравнений»

2.2.5. Какой способ решения систем мы еще не вспомнили? (графический)

Что является графиком линейного уравнения? (прямая линия).

Сколько точек нужно для построения прямой линии? (две)

Кто напомнит алгоритм решения систем графическим способом?

• Построить графики каждого из уравнений системы;

• Найти координаты точки пересечения построенных прямых (если они пересекаются)

Какие возможны случаи взаимного расположения прямых на плоскости?

1. Прямые пересекаются, т.е. имеют одну общую точку. Тогда система имеет единственное решение.

2. Прямые параллельны, т.е. не имеют общих точек. Тогда система уравнений не имеет решений.

3. Прямые совпадают. Тогда система уравнений имеет бесконечно много решений.

Задание ( на доске): Решить графически следующую систему

Проверьте правильность выполнения задания (Слайд №14)

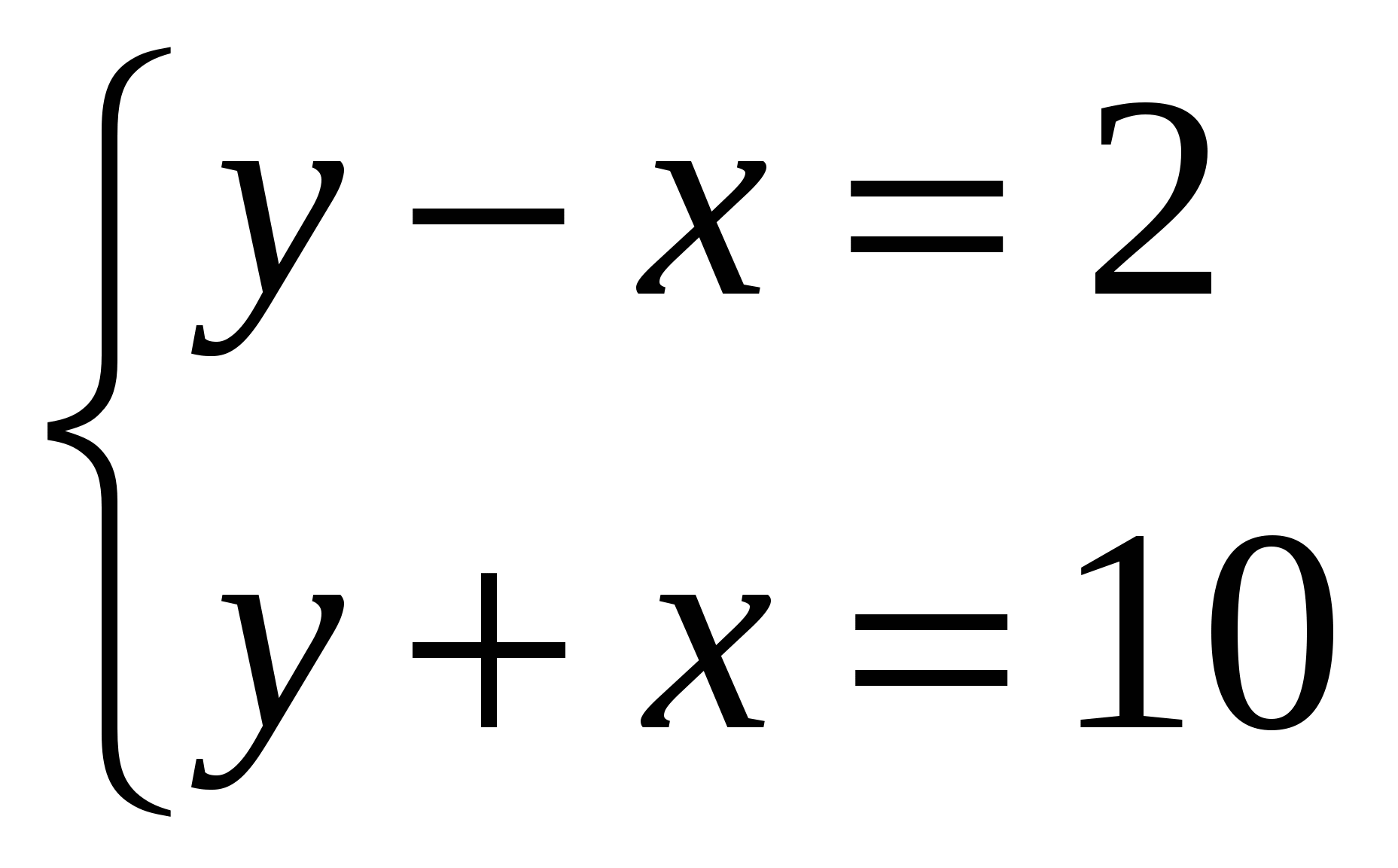
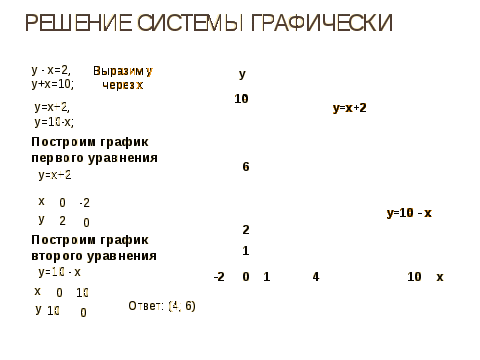
4. Подведение итогов урока.

1. Оценки за урок.

Посчитайте количество ваших баллов и поставьте в оценочный лист оценку за урок. Критерии оценки:

10 -12 баллов – «5»

8 – 9 баллов – «4»

Менее 9 баллов – «3»

2. Домашнее задание : стр. 164 «Проверь себя»

Дополнительно: №674(2), №675(2), №678

3. Рефлексия. Заполнить барометр настроения.

Приложение 1

Барометр настроения

Поставь крестик, как ты провел урок:

Приложение 2

Оценочный лист

Фамилия_________________________

Имя_______________________

Этапы

урока

Задания			Количество баллов
II	Домашнее задание		№658
			№666
III	Устные упражнения
IV	Решение задач	Определения
		№671(1)
		№671(2)
		№672(1)
		№677
Итоговое количество баллов
Итоговая оценка

Приложение 3

Из истории возникновения уравнений

Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Издавна применялось исключение неизвестных из линейных уравнений. В XVII - XVIII в.в. приемы исключения разрабатывали Лейбниц, Эйлер, Безу, Лагранж.