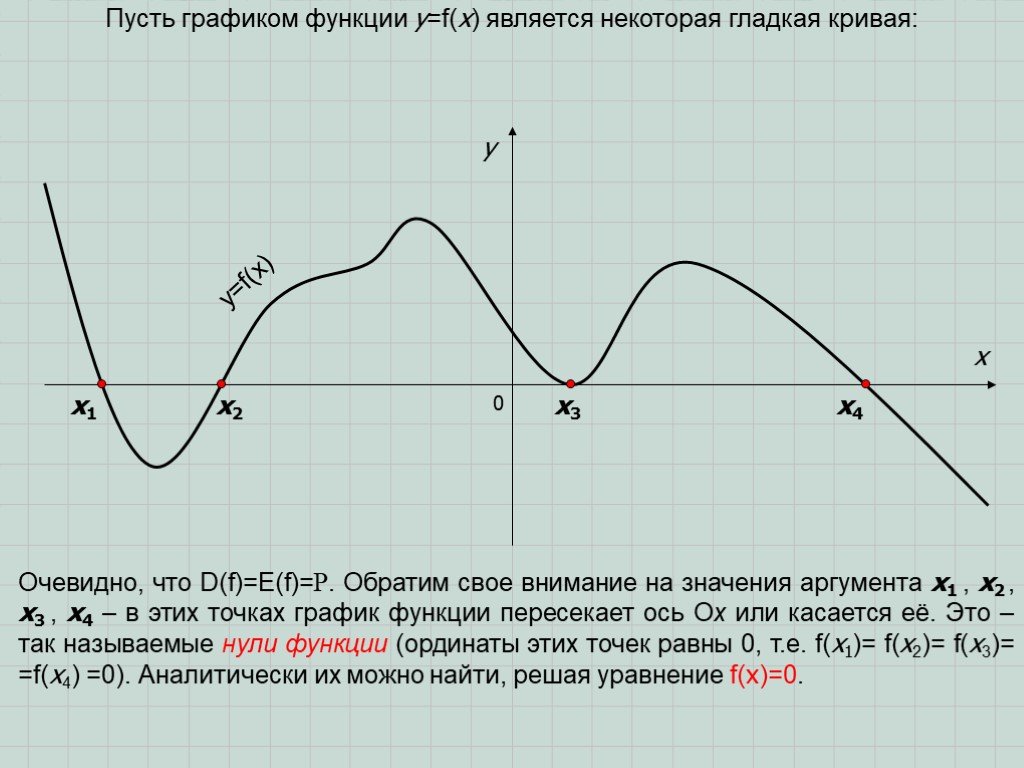
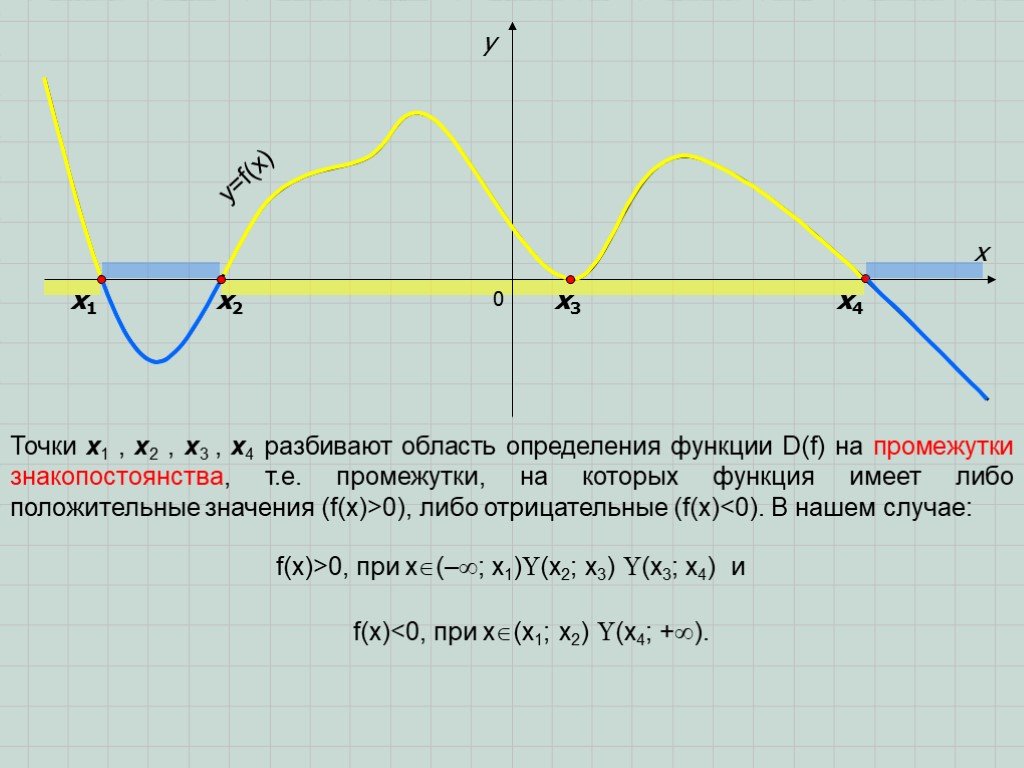
Презентация "Решение неравенств методом интервалов" по математике – проект, доклад

Решение неравенств методом интервалов.

Алгебра и начала анализа, 10 класс.

Воробьев Леонид Альбертович, г.Минск

0 x y

Пусть графиком функции y=f(x) является некоторая гладкая кривая:

y=f(x)

Очевидно, что D(f)=E(f)=. Обратим свое внимание на значения аргумента x1 , x2 , x3 , x4 – в этих точках график функции пересекает ось Ох или касается её. Это – так называемые нули функции (ординаты этих точек равны 0, т.е. f(x1)= f(x2)= f(x3)= =f(x4) =0). Аналитически их можно найти, решая уравнение f(x)=0.

х4 х3 х1

Точки x1 , x2 , x3 , x4 разбивают область определения функции D(f) на промежутки знакопостоянства, т.е. промежутки, на которых функция имеет либо положительные значения (f(x)>0), либо отрицательные (f(x)<0). В нашем случае:

f(x)>0, при х(–; х1)(х2; х3) (х3; х4) и

х2

f(x)<0, при х(х1; х2) (х4; +).

Опираясь на эту геометрическую иллюстрацию, мы можем вывести алгоритм решения неравенств, получивший название «метод интервалов».

Методом интервалов можно решить любое неравенство вида: f(x)0. При решении придерживаются следующей схемы (перепишите её в тетрадь!):

Найти D(f); Найти нули функции, решая уравнение f(x)=0; Отметить на D(f) все полученные нули; Определить знак функции на каждом полученном промежутке; Записать ответ, выбрав промежутки с соответствующим знаком.

Проиллюстрируем данную схему на нескольких примерах. Пример 1. Решите неравенство .

Решение. Под функцией f(x) следует понимать выражение в левой части неравенства. Это дробно-рациональная функция. 1) D(f)=, кроме х= – 4; 2 (данные значения обращают знаменатель в нуль) .

2) Найдем нули функции. Значение дроби равно нулю, если числитель этой дроби равен нулю, т.е. х= –1; 3; 7 – нули функции. 3) Обратите внимание, что точки разрыва функции (–4 и 2) всегда на числовой прямой будут пустыми (или «выколотыми»), а нули функции – в зависимости от знака неравенства (если знак неравенства строгий, то точки пустые, если нестрогий, то обычные).

–4 2 х –1 3 7 +

■ на остальных промежутках (двигаемся от крайнего справа промежутка влево) знаки расставляются по правилу: знак по сравнению с предыдущим меняется, если показатель степени линейного множителя нечетный и не изменяется, если показатель степени линейного множителя четный. В нашем случае получается… (см.рис.).

(х–3) (х–7) (х+1) (х–2) (х+4) 4 –

Вышеизложенный метод определения знаков на интервалах по сути опирается на понятие «кратных» корней. Если Вам этот термин не знаком, то можно воспользоваться другим способом:

■ выбирая из каждого промежутка любое значение, подставляют в формулу, задающую данную функцию и определяют по полученной комбинации знак функции на каждом промежутке:

Как Вы можете убедиться – результат расстановки знаков такой же, как в предыдущем способе.

5) Остается записать ответ, выбрав промежутки соответствующие знаку неравенства. В нашем случае, знаку «» соответствуют промежутки со знаком «+». Важно не забыть х=3!!!

Ответ: х[–1; 2){3}[7; +).

Пример 2. Решите неравенство .

Решение. Перенесем все в левую часть неравенства: . 1) D(f)=, кроме х= – 1; 1, где f(x)= ;

2) Нулей функции нет, т.к. дискриминант квадратного трехчлена отрицательный;

3) – 1 1

4) Проверьте себя, как Вы поняли правило расстановки знаков…

5) Ответ: х(–1; 1).

Пример 3. Решите неравенство sinx+cos(2x)>1.

Решение. Перепишем неравенство в виде: sinx >1 – cos(2x). Используя формулы половинного аргумента, получим: sinx >2sin2x или 2sin2x – sinx<0.

1) D(f)=, где f(x)=2sin2x – sinx;

3) Расставим полученные нули функции на числовой прямой:

Учитывая периодичность функции y=sinx, достаточно ограничиться отрезком длиной 2;

4) Расставим знаки на полученных промежутках;

5) Запишем ответ: