Презентация "Арксинус. Решение уравнения sin t = a" (10 класс) по математике – проект, доклад
Презентацию на тему "Арксинус. Решение уравнения sin t = a" (10 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
Графическое решение линейного уравнения с двумя переменными
Цель урока:. проверить прочность знаний, умений и навыков, учащихся по данной теме, обеспечить закрепление и обобщение изученного материала; развивать ...Решение биквадратного уравнения
Цель урока:. образовательная: изучить приемы решения биквадратного уравнения, рассмотреть способ замены при решении уравнений; развивающая: развитие ...Арккосинус и решение уравнения cos x = a
Цели урока. ввести понятие arccos x; вывести формулу решения уравнения cos x=a, ; рассмотреть уравнения на применение этой формулы; рассмотреть простейшие ...Решение заданий С2 ЕГЭ-2010
Задача №1:. В прямоугольной системе координат заданы точки O(0;0), D(-5;0), C(0;-12). Найдите площадь боковой поверхности конуса, полученного вращением ...Различные виды уравнения прямой
Общее уравнение прямой. Уравнение Ax+By+C=0 (где A, B и C могут принимать любые значения, лишь бы коэффициенты A, B не были равны нулю оба сразу) ...Проверка корней тригонометрического уравнения
В основу метода проверки корней тригонометрического уравнения следует положить понятие периода уравнения. Пусть дано, например, уравнение: Легко заметить, ...Показательные уравнения и способы их решения
Определение: Показательные уравнения – уравнения, в которых переменная входит только в показатели степеней при постоянных основаниях. Например,. Основные ...Показательные уравнения
Показательные. Цели урока: 1. ввести понятие показательных уравнений; 2. формировать умение решать показательные уравнения основными методами: функционально-графическим, ...Определение квадратного уравнения. Неполные квадратные уравнения
Тема урока: «Определение квадратного уравнения. Неполные квадратные уравнения» Цели урока: - познакомить учащихся с квадратными уравнениями в общем ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...Арксинус, арккосинус, арктангенс и арккотангенс
Функция у = sin x 0 y=sin x. Функция y=sin x возрастает на отрезке. 1. Арксинус а b Для любого в промежутке. существует единственный корень b уравнения ...Алгебраические уравнения произвольных степеней
Алгебраические уравнения произвольных степеней. 1. Введение. Всякий школьник, прежде всего, умеет решать уравнение первой степени: если дано уравнение ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Алггоритм. Решение задач
Задача 1. В урне хранится некоторое количество чёрных и белых шаров. Требуется разложить эти шары по двум корзинам чёрного и белого цвета: белые шары ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Решение задач
Восстанови ряд чисел:. 1 + 2 10 – 2 3 + 1 8 - 1 2 + 2 9 – 2 4 + 1 7 - 1 3 + 2 8 – 2 ……. ……. ……. …… ……. ……. …… …… …… ……. Угадай пример:. 10 8 9 2 2 ...Блиц-опрос "Решение треугольников"
Выбери вопрос. В треугольнике АВС угол А равен 40 градусов. Внешний угол при вершине В равен 68 градусов. Найдите угол С. Угол С равен 28 градусов. ...Решение задач В1
Сырок стоит 7 руб. 30 коп. Какое наибольшее число сырков можно купить на 70 рублей? Проверка. 7 руб 40 коп=7,4 руб 70:7,4≈ 9,45… Ответ: 9 сырков. ...Вывод канонического уравнения эллипса
Цели и задачи. Цели: Рассмотреть основные понятия по теме «Вывод канонического уравнения эллипса» Задачи: Рассмотреть свойства эллипса Исследовать ...Конспекты
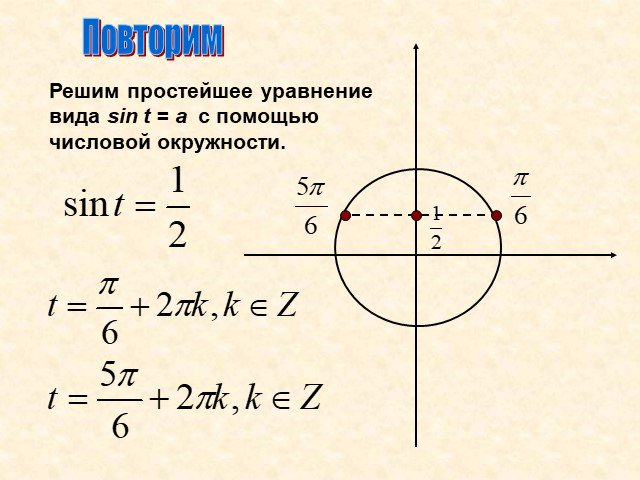
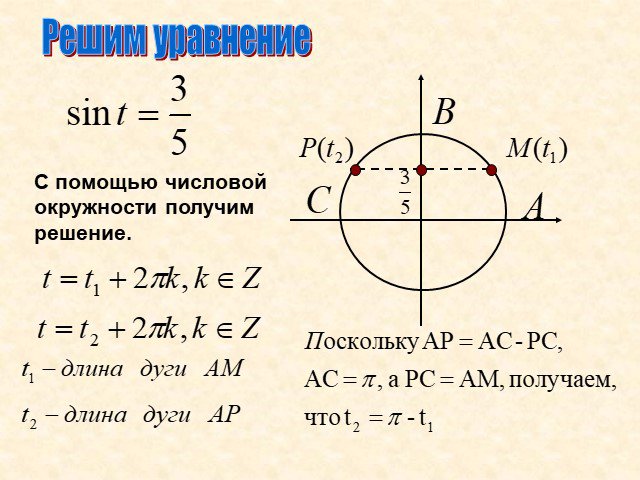
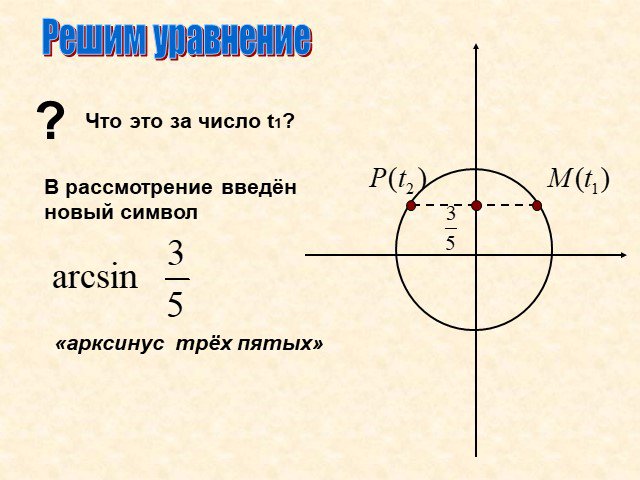
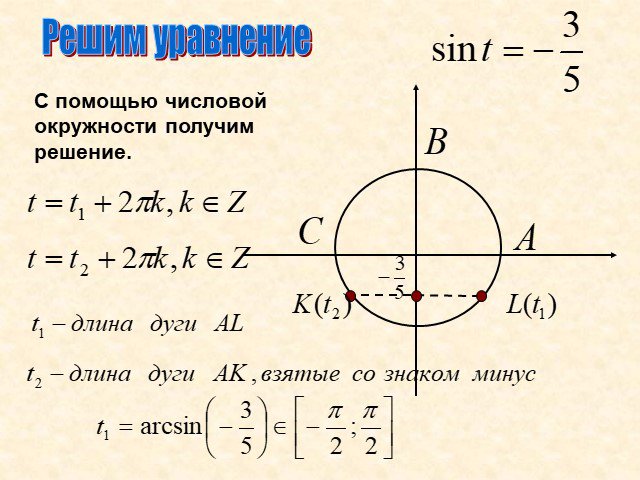
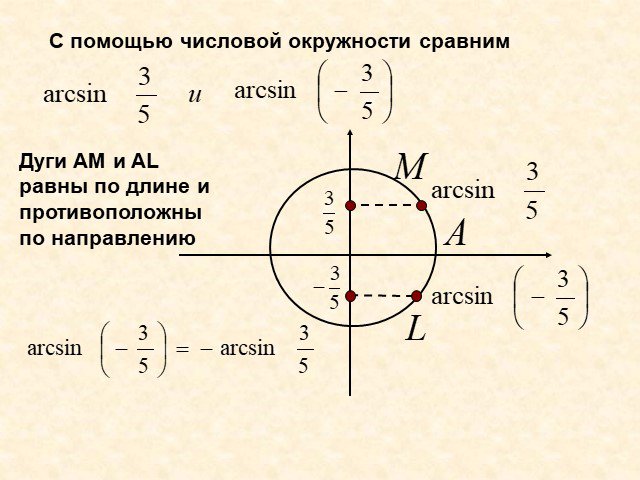
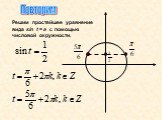
Арксинус. Решение уравнения sin t =a
Муниципальное общеобразовательное учреждение. «Гимназия №87» города Саратова. Методическая разработка. . урока по теме. . «Арксинус. ...Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений
Тема урока: Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений. Цели урока:. Образовательные. :. . ...Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений
Тема:. «Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений». Тип урока:. урок изучения нового материала. Цели урока:. ...Знакомство с уравнениями. Решение уравнений методом подбора
Урок математики во 2 классе. Тема: Знакомство с уравнениями. Решение уравнений методом подбора. Цели урока:. . Обучающие:. открыть вместе ...Итоговое повторение. Решение заданий по теме « Уравнения
Урок по теме. « Итоговое повторение. Решение заданий по теме « Уравнения»». Учитель :. Петрученя Н. В.,. учитель математики. МБОУ «Засосенская ...Показательные уравнения
ТЕМА «Показательные уравнения». Цели:. 1.Познакомиться с разными видами показательных уравнений, научиться различать разные виды показательных уравнений, ...Порядок выполнения действий в выражениях без скобок и со скобками. Решение задач выражением
Технологическая карта урока математики. . Класс:. 3а. Учитель:. Северьянова Е.М. Программа:. УМК «Гармония». Тема урока: «. Порядок выполнения ...Обобщение. Сложение и вычитание в пределах 20. Решение примеров
«Обобщение. Сложение и вычитание в пределах 20. Решение примеров.». Конспект урока по математике. . учителя начальных классов. первой квалификационной ...План урока по теме: Квадратные уравнения
План урока по теме : Квадратные уравнения (8 класс). Автор Шаповалова Светлана Эдуардовна. Учитель МБОУ СОШ № 50 им.С.В.Марзоева г.Владикавказ. ...Логарифмические уравнения и неравенства
Тема. : «Логарифмические уравнения и неравенства». Цели: Проверить теоретические и практические знания по теме; отработать навыки решения логарифмических ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:26 октября 2015
Категория:Математика
Классы:
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию