Конспект урока «Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений» по математике
Тема урока: Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений
Цели урока:
-
Образовательные:
-
сформировать понятие о квадратном уравнении вида ax2 + bx + с = 0;
-
его коэффициентах а и b и свободном члене с;
-
познакомить учащихся с приведенным квадратным уравнением;
-
изучить определение неполного квадратного уравнения;
-
вырабатывать навыки решения неполных квадратных уравнений.
-
Развивающие:
-
развитие логического мышления, памяти, внимания;
-
развитие умения сравнивать, обобщать, формулировать учебно-познавательную мотивацию с помощью интересных задач.
-
Воспитательные: воспитание трудолюбия, математической культуры.
ХОД УРОКА
I. Организационный момент
Сообщение темы и целей урока.
II. Проверка домашней работы
1. Устно:
а) Что называется уравнением?
б) Что называется корнем уравнения?
в) Что значит решить уравнение?
III. Изучение нового материала
Решим вместе
(3х-5)(2х+3)=0
Так как правая часть уравнения равна нулю, то воспользуемся способом «расщепления»:
3х-5=0 или 2х+3=0
3х=5 2х = - 3
х1 = 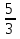 х2 = -
х2 = - 
Возникает вопрос можно ли решить этим способом уравнение
(3х-5)(2х+3)=-13? Нельзя, потому что справа стоит не нуль.
Упростим это уравнение:
(3х-5)(2х+3)=-13
6х2 +9х – 10х – 15 = - 13 раскрыли скобки
раскрыли скобки
6х2 +9х – 10х – 15+13 = 0  перенесли все слагаемые в левую часть уравнения
перенесли все слагаемые в левую часть уравнения
6х2 – х -2 = 0  привели подобные слагаемые
привели подобные слагаемые
В этом уравнение присутствует х2, поэтому его называют квадратным.
Заполним таблицу «Квадратные уравнения»
| | Определение | Пример |
| Квадратное уравнение ах2 +bx +c = 0 | Уравнение называют квадратным, если его можно записать в виде ах2 +bx +c = 0, где х – неизвестное, а,b,с – заданные числа и а Название коэффициентов: а – первый, или старший, коэффициент, b - второй коэффициент, с – свободный член. Левая часть квадратного уравнения называется квадратным трехчленом. | 3х2 +5x -12 = 0 а= 3,b = 5,с = -12 |
| Приведенное квадратное уравнение х2 +px +q = 0 | Приведенным квадратным уравнением называется уравнение, у которого коэффициент при х2 равен 1. Замечание. Любое квадратное уравнение можно превратить в равносильное приведенное, разделив его левую и правую части на а: х2 + | х2 +7x -9 = 0 a = 1,b = 7,с = -9 |
| Неполные квадратные уравнения
| Если в квадратном уравнении ах2 +bx +c = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называется неполным квадратным уравнением.
| -2х2=0, a = -2, b=0, c=0, 4х2 +7x = 0, a = 4, b=7, c=0, -х2 -5 = 0, a = -1, b=0, c= -5, |
3. Решение неполных квадратных уравнений в общем виде.
Вместе с учителем учащиеся записывают в тетрадях в таблицу схему решения каждого вида неполного квадратного уравнения:
| Количество корней | Решение | Пример | |
| ах2=0 | Один корень (два совпадающих) | ах2=0, х=0 | 8х2=0 х=0 |
| ах2 +bx = 0 b | Два корня | ах2 +bx = 0 x(ах +b)=0 х1=0 или ах +b=0 х2= - | 2х2 +14x = 0 2x(х +7)=0 2x = 0 (х +7)=0 х1=0 или х +7=0 х2= - 7 х2 - 5x = 0 x(х -5)=0 х1=0 или х - 5=0 х2= 5 |
| ах2 +c = 0 с | Либо два корня, либо корней нет | ах2 +c = 0 ах2 = - c х2 = -
х1 = х2 =
корней нет |
3х2 = 27 х2 = 9, 9 х1 = х2 =
3х2 = -7 х2 = - - |
Вывод: Неполное квадратное уравнение может иметь 2 корня, 1 корень, не иметь корней.
Типовые задания.
а) 5 = 5+4х2,
б) 17х2 = - 3,
в) 16х = 3х2 – 2х,
г) 3х2 - 14 = 30 - 8х2,
д) (х - 5)(х + 3) + х2 = (х - 8)(х + 6).
Историческая справка
Обратимся к историческому путеводителю.
Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными относятся во второму тысячелетию до н.э. Это эпоха расцвета Вавилонии и Древнего Египта.
Первое тысячелетие н.э. – Римские завоевательные войны. К этому периоду относится творчество Диофанта. Его трактат “Арифметика” содержит ряд задач, решаемых при помощи квадратных уравнений. В IX веке узбекский математик Аль-Хорезми в Трактате “Алгебра” классифицирует квадратные уравнения. Для нас это время знаковое тем, что приблизительно в это время образуется древнерусское государство Киевская Русь.
Все это время отличные по записи уравнения считались различными. Не было единого подхода к их решению.
И только в XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Тем самым заложил основы буквенной алгебры.
Более подробно с этапами развития методов решения квадратных уравнений, а так же личностью Виета и его вклада в развитие алгебры мы сможем познакомиться на конференции.
Подведение итогов.
Итак, подведем итог.
Решение квадратных уравнений, возможно, осуществлять разными методами. Сегодня мы рассмотрели способы решения неполных квадратных уравнений. На следующих уроках мы будем учиться решать и другие виды квадратных уравнений. Я хочу закончить сегодняшний урок словами Яна Амоса Каменского: «Учиться нелегко, но интересно». Думаю, что эти слова подходят для окончания нашего урока, Спасибо, желаю успехов!
Литература:
-
Научно-популярное издание Энциклопедия для детей. Т 11. Математика. М. - Аванта+,1997
-
Алгебра за 7 занятий.8 класс: пособие для обучающихся общеобразовательных организаций/ Н.В. Лахова. – М.: Просвещение.
-
Ершова А.П., Голобородько В.В., Крижановский А.Ф. Тетрадь – конспект по алгебре для 8 класса.- М.: ИЛЕКСА 2012.
Здесь представлен конспект к уроку на тему «Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

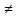 0
0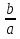
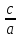 = 0
= 0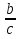
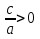 , то
, то 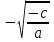
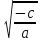
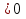 , то
, то 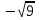 = - 3
= - 3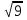 = 3
= 3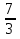 ,
, 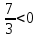 , то корней нет
, то корней нет