Презентация "Решение заданий С2 ЕГЭ-2010" по математике – проект, доклад
Презентацию на тему "Решение заданий С2 ЕГЭ-2010" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
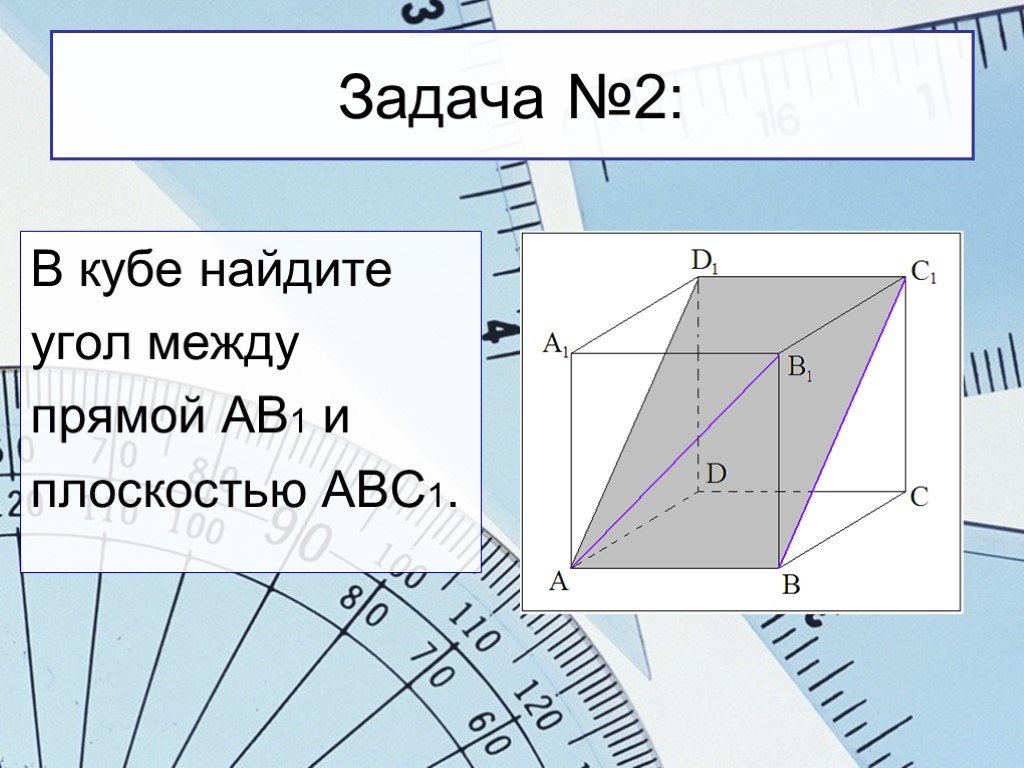
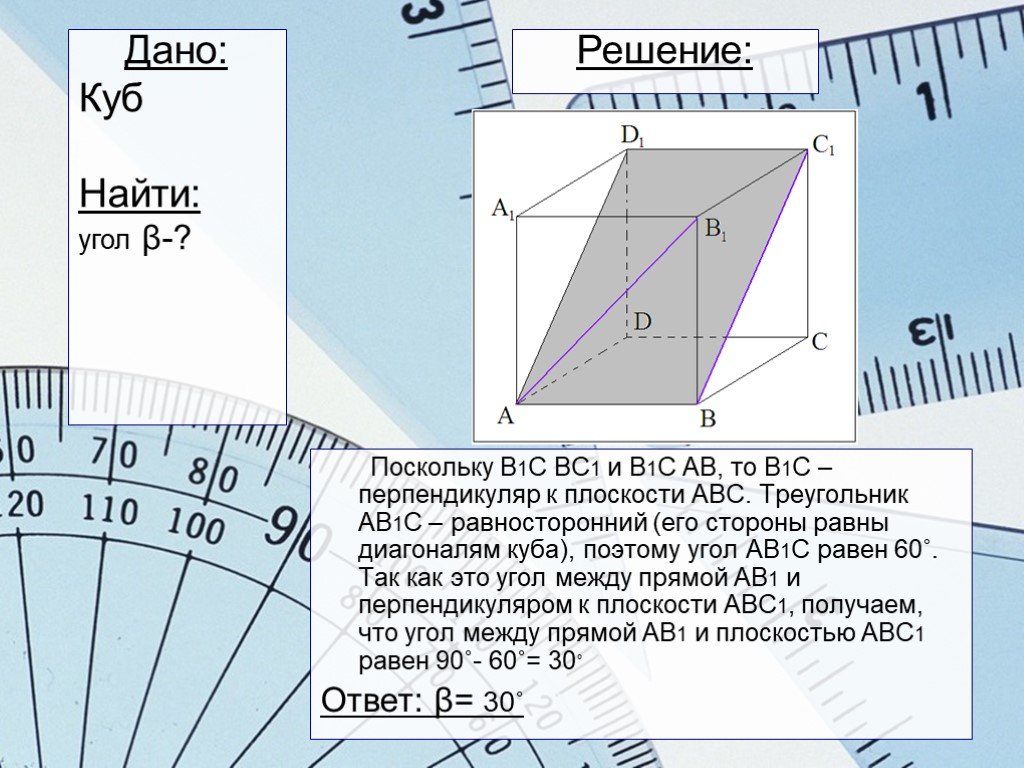
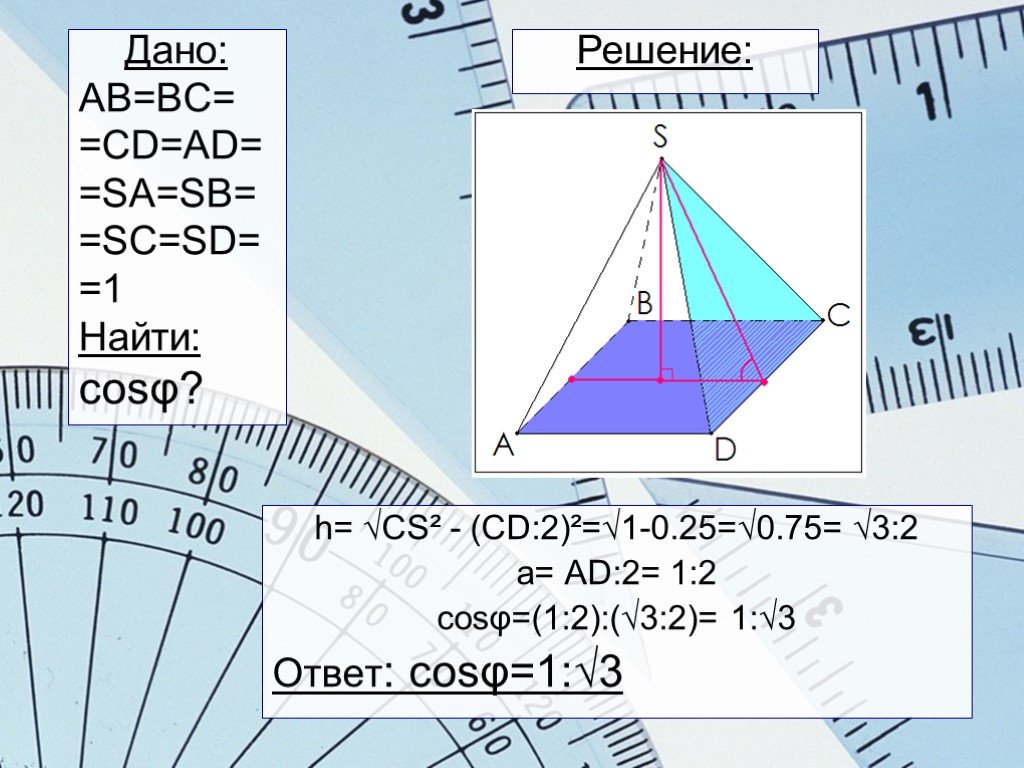
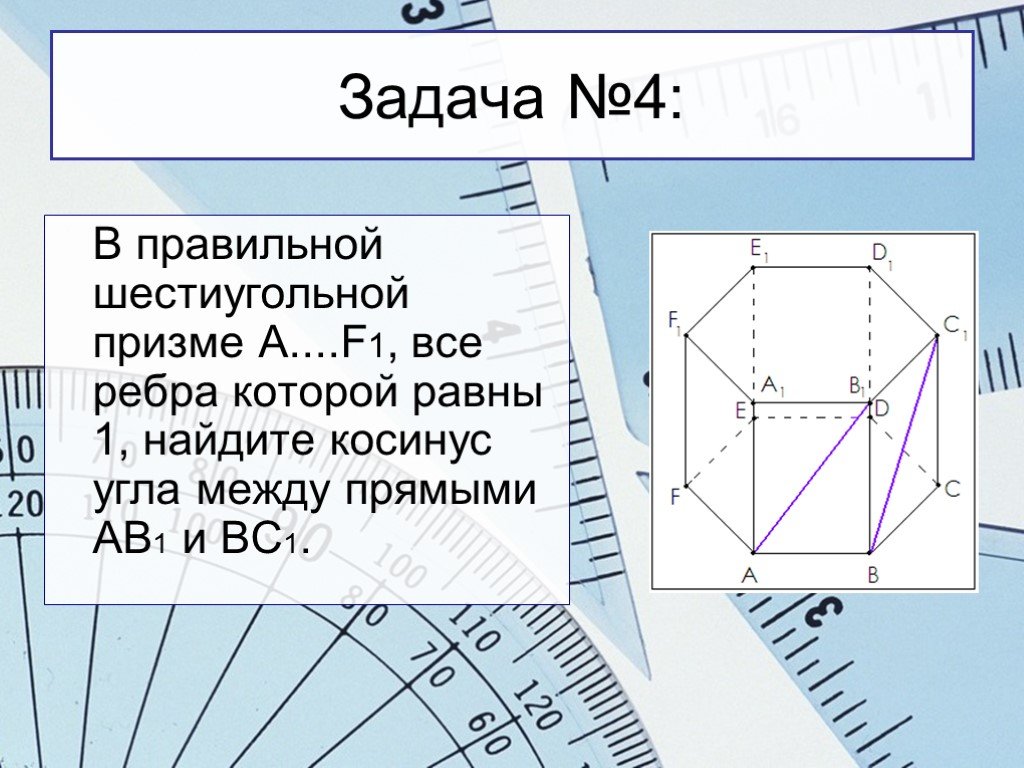
Слайды презентации
Список похожих презентаций
Решение заданий ЕГЭ математика В6
В А С катет гипотенуза. . Теорема Пифагора: Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Основное тригонометрическое ...Решение заданий с модулем и параметром
Цель занятия:. _ закрепить полученные знания об исследованиях квадратного трёхчлена; - Изучить графический способ решения заданий с модулем и параметром. ...Подготовка к ЕГЭ по математике. Решение заданий В12
Проверяемые требования (умения). Уметь строить и исследовать простейшие математические модели. Прототипов заданий В12 – 25. Умения по КТ. Моделировать ...Решение заданий В10 по материалам открытого банка задач ЕГЭ по математике
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Решение. ...Решение задач по теме:«Отношения. Масштаб.»
Задача № 1. Дан отрезок АВ, на нем взяты точки С и Д так, что АС : СД : ВД = 3 : 5 :4. Чему равно отношение: АС : АВ, СД : АВ, ВД : АВ, АС : ВС, АД ...Решение задач с помощью блок-схем
Что такое алгоритм? Чем отличается алгоритм от алгоритмизации? Свойства алгоритма? Виды алгоритмов? Если углы вертикальные, то они равны. 1 2. Определить ...Решение задач на расчет пути, времени и скорости
Повторение материала. Как обозначается скорость? В каких единицах измеряется скорость? Как обозначается путь? В каких единицах измеряется путь? Как ...Решение задач по математике
Можно считать несчастным тот день, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию. Ян Амос Коменский. Задачи:. Образовательная ...Решение задач на применение аксиом стереометрии и их следствий
Математический диктант. Как называется раздел геометрии, изучающий фигуры в пространстве? Назовите основные фигуры в пространстве. Сформулируйте аксиому ...Решение задач на пропорциональное деление
Мотивация к учебной деятельности. Перемена пролетела, Дверь певуче заскрипела. Мы вошли тихонько в класс И урок начнём сейчас. Актуализация знаний. ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Решение задач части В
Схема решения практико-ориентированных задач. Прочитать задачу, обдумать метод решения Решить задачу Проверить решение на соответствие реальным условиям ...Вычитание. Решение задач с помощью действия вычитания
Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...Варианты заданий ЕГЭ по математике
Структура работы по математике. На выполнение экзаменационной работы по математике дается 4 часа (240 минут). В работе 30 заданий. Они распределены ...Блиц-опрос "Решение треугольников"
Выбери вопрос. В треугольнике АВС угол А равен 40 градусов. Внешний угол при вершине В равен 68 градусов. Найдите угол С. Угол С равен 28 градусов. ...Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...Решение задач с помощью ППП EXCEL
. . 5. Нажмите F2, а затем комбинацию клавиш CTRL+SHIFT+ENTER. В результате появится таблица:. . Регрессионная статистика выводится в следующем порядке:. ...ГИА-2014 (геометрия). Решение задач на углы.
Повторение к ГИА. http://79.174.69.4/os/xmodules/qprint/afrms.php?proj. Углы в треугольниках. № 035C64 Ответ: 8. Центральный угол AOB опирается на ...Решение задач с помощью уравнений
Что такое уравнение? Уравнение – это равенство, содержащее переменную, значение которой надо найти. Что называется корнем уравнения? Корнем уравнения ...Конспекты
Итоговое повторение. Решение заданий по теме « Уравнения
Урок по теме. « Итоговое повторение. Решение заданий по теме « Уравнения»». Учитель :. Петрученя Н. В.,. учитель математики. МБОУ «Засосенская ...Контрольная работа по теме «Использование метода координат в пространстве для решения заданий С2 ЕГЭ
Конспект урока по теме «. Контрольная работа по теме «Использование метода координат в пространстве для решения заданий С2 ЕГЭ»». Автор:. Макарова ...Решение задач на вычисление объема цилиндрических и конических тел
Урок 5. Тема урока:. Решение задач на вычисление объема цилиндрических и конических тел. Тип учебного занятия:. Обобщение и систематизация знаний ...Решение задач в два и три действия на все арифметические действия
. КГУ «СШ № 44». г. Петропавловск. МАТЕМАТИКА. 3 класс. . ТЕМА:. РЕШЕНИЕ ЗАДАЧ В ДВА И ТРИ ДЕЙСТВИЯ НА ВСЕ АРИФМЕТИЧЕСКИЕ ...Решение задач и числовых выражений
Урок 45. Математика 1 класс. Тема: «Решение. задач и числовых выражений. ». Цели урока. :. в ходе выполнения различных заданий закреплять умение ...Решение задач
Тема урока:. Поупражняемся в вычислениях и повторим пройденное по теме «Решение задач». Цели урока:. . Образовательная: повторить и обобщить умения ...Решение задач
Тема: Решение задач. Предмет: Математика. Класс: 1 класс. Цели урока:. Обобщить знания о задачах на увеличение и уменьшение числа, на разностное ...Решение задач на концентрацию и процентное содержание
. Липчанская Ирина Рифовна. учитель математики. . МБОУ «СОШ № 4 МО «Ахтубинский район». Урок по теме «Решение задач на концентрацию и ...Решение задач на нахождение периметра прямоугольника
РОССИЙСКАЯ ФЕДЕРАЦИЯ. КРАСНОЯРСКИЙ КРАЙ. АДМИНИСТРАЦИЯ ГОРОДА НОРИЛЬСКА. УПРАВЛЕНИЕ ОБЩЕГО И ДОШКОЛЬНОГО ОБРАЗОВАНИЯ. МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ...Длина. Решение задач
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа №54. го Тольятти Самарской области. КОНСПЕКТ. урока ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 апреля 2019
Категория:Математика
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию