Презентация "Определение квадратного уравнения. Неполные квадратные уравнения" по математике – проект, доклад
Презентацию на тему "Определение квадратного уравнения. Неполные квадратные уравнения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 10 слайд(ов).
Слайды презентации
Список похожих презентаций
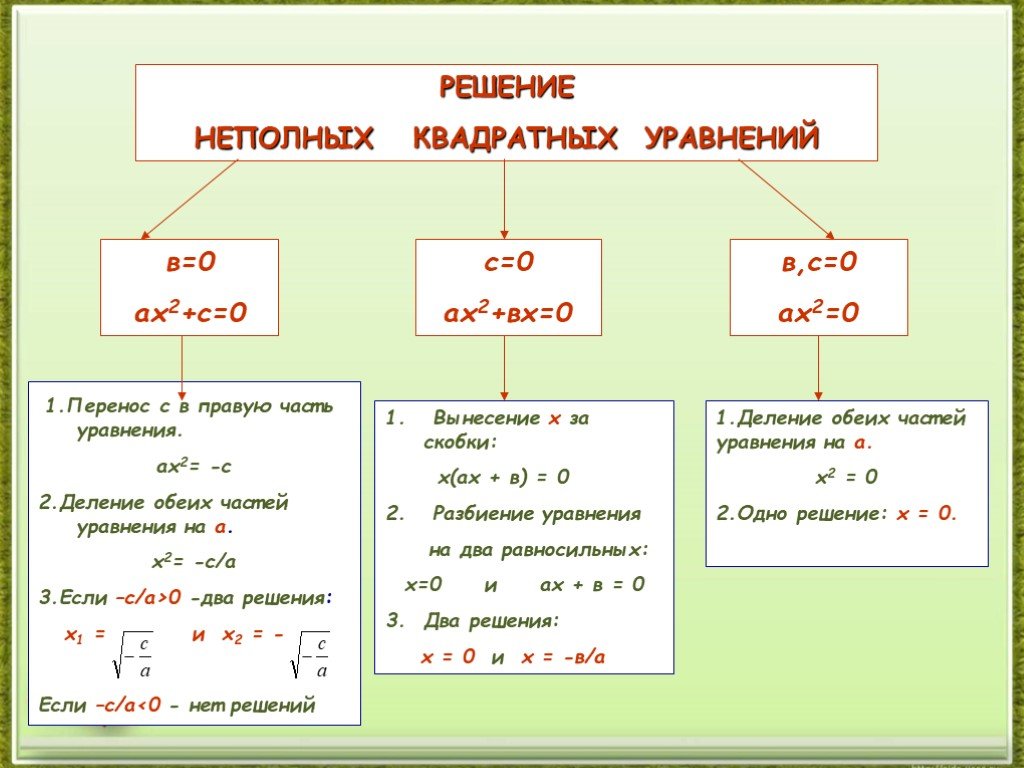
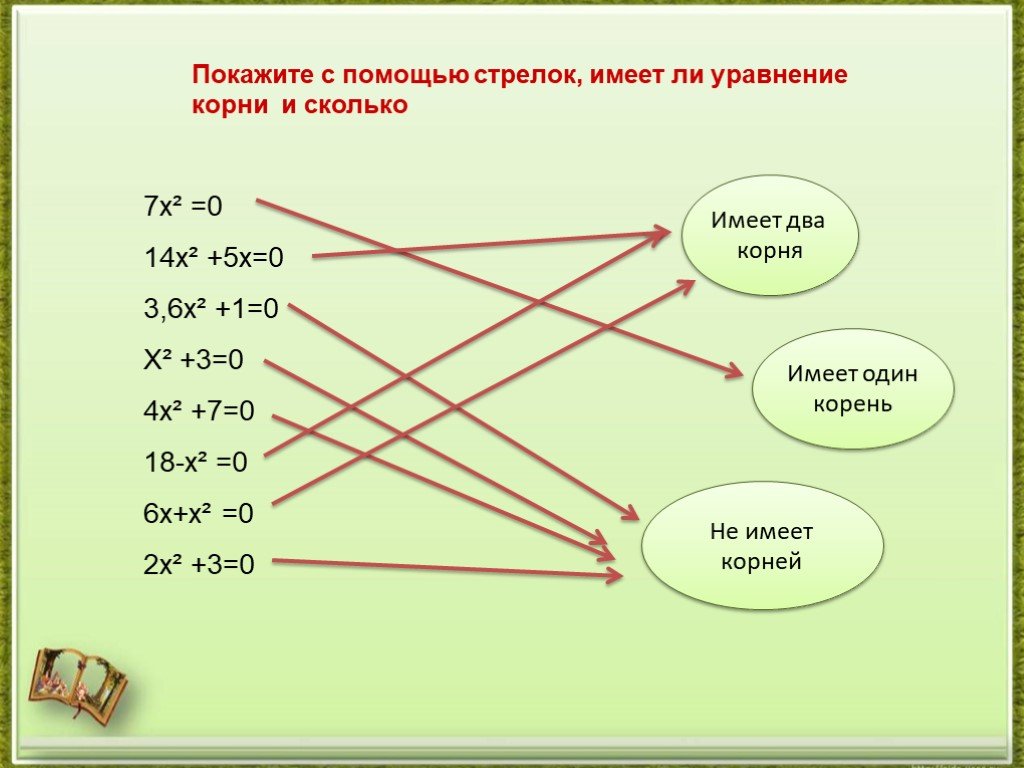
Определение квадратного уравнения. Неполные квадратные уравнения
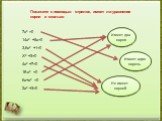
ax+b=0. 1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0.1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...
Определение квадратного уравнения. Неполные квадратные уравнения
Решите уравнения Х=±2 Х=± Корней нет Х=0 Х=0,Х=2. 5х-2=0. Разделите данные уравнения на две группы. Какие уравнения называются квадратными? 1. Уравнение ...Определение квадратного уравнения. Неполные квадратные уравнения.
Эпиграф: Чтобы решить уравненье, Корни его отыскать, Нужно немного терпенья, Ручку, перо и тетрадь. Этапы подготовки:. Разбились на группы, которые ...Квадратное уравнение. Неполные квадратные уравнения
Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной ...Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлена на множители
Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной. Содержание. Квадратный ...Неполные квадратные уравнения
"Мне приходится делить своё время между политикой и уравнениями. Однако уравнения по-моему, гораздо важнее, потому что политика существует только ...Неполные квадратные уравнения
Устный счёт. а) Вычислить: 32 , (-2)2,. б) Решить уравнения, сколько корней они имеют? X2 = 4 x2= - 16 3x2 = 0 в) Разложить на множители: x2 - 4 2x2 ...Неполные квадратные уравнения
Математику нельзя изучать, наблюдая, как это делает сосед! А. Нивен. 1. Какое уравнение называется квадратным? 2. Может ли коэффициент а в квадратном ...Как решать неполные квадратные уравнения
Тема урока: Решение неполных квадратных уравнений. Покупка билетов. Вариант – 1. Решить уравнение:. Вариант – 2. Решить уравнение:. Устная работа. ...Квадратные уравнения
Содержание. Определение квадратного уравнения;. Решение неполных квадратных уравнений;. Решение уравнений, сводящихся к неполным квадратным уравнениям;. ...Квадратные уравнения
Тема урока:. Решение квадратных уравнений. Цели урока: Научить учеников решать квадратные уравнения. Научить учеников изпользовать более легкий способ ...Квадратные уравнения урок
Цели урока: систематизировать и обобщить знания учащихся по теме «Решение квадратных уравнений»; развивать логическое мышление; повышать интерес к ...Полные квадратные уравнения
Уравнение вида ax2+bx+c=0,где левая часть называется квадратным трехчленом относительно х, у которого a,b,c,- данные числа, причем a≠0, а правая часть ...Квадратные уравнения и уравнения, приводимые к квадратным
Расписание. 1. Алгебра 2. История 3. География 4. Рисование. Алгебра. Выбрать лишнее уравнение:. 1. 3х2−х-7 = 0, 2. х2 − 89 = 0, 3. 4х2 + х −3 = 0, ...Решение квадратного уравнения
Формула корней квадратного уравнения. Устный счёт. 1.Определить по какому признаку написаны уравнения и какое из них лишнее и почему? Решить устно ...Понятие квадратного уравнения
определение. Уравнение вида ах2+вх+с=0, где а,в,с – числа, а≠0, называется квадратным. Какие из уравнений являются квадратными. 1. 2х2+7х-3=0 2. 5х-7=0 ...Приёмы устного решения квадратного уравнения
Цель: устные приёмы эффективного решения квадратных уравнений. Алгоритм. Извлечения квадратного корня Из натурального числа. 92 *16 =96 81 1116 1116 ...Квадратные уравнения
Квадратное уравнение имеет действительные положительные корни, если. Квадратное уравнение имеет действительные отрицательные корни, если. Квадратное ...Решение биквадратного уравнения
Цель урока:. образовательная: изучить приемы решения биквадратного уравнения, рассмотреть способ замены при решении уравнений; развивающая: развитие ...Конспекты
Определение квадратного уравнения. Неполные квадратные уравнения
ПЛАН-КОНСПЕКТ УРОКА «Определение квадратного уравнения. Неполные квадратные уравнения». . . ФИО (полностью). . Перькова Ирина Васильевна. ...Определение квадратного уравнения. Неполные квадратные уравнения
План-конспект. урока по математике в 8 классе. «Определение квадратного уравнения. Неполные квадратные уравнения». Составила учитель ...Неполные квадратные уравнения
. Конспект урока по алгебре в 8 классе по учебнику Г. В. Дорофеева и другие на тему "Неполные квадратные уравнения". . Урок закреплении и обобщения ...Квадратные уравнения. Неполные квадратные уравнения
ПЛАН-КОНСПЕКТ УРОКА. ФИО:. Вершинина Ольга Сергеевна. . Место работы:. МДОУ «СОШ № 12 имени Сметанкина В.Н.». . Должность:. учитель. . Предмет:. ...Неполные квадратные уравнения
Автор материала: Маслова Наталья Васильевна. . Место работы МБОУ ООШ №34 г. Белгород. . Должность автора: учитель математики и информатики. ...Биквадратные уравнения
Иванова Ольга Александровна. МОУ «СОШ №2» г. Всеволожска. Учитель математики. Урок по теме: «Биквадратные уравнения». Цели урока:. . Обучающие:. ...Квадратные уравнения
Муниципальное казенное общеобразовательное учреждение. «Ширинская средняя общеобразовательная школа». . Модульный урок математики. . в ...Способы решения квадратного уравнения. Использование частных соотношений коэффициентов
Урок в 8 классе по алгебре с применением технологии критического мышления в процессе преподавания математики. Тема: «Способы решения квадратного ...Квадратные уравнения
Урок – обобщение по теме «Квадратные уравнения». Конева Надежда Александровна, учитель математики ВКК. . МБОУ Борисоглебского городского округа. ...Квадратные уравнения
Урок на тему «Квадратные уравнения». Цели урока:. . - в игровой форме проверить умение учащихся решать квадратные уравнения. - повторить пройденный ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:13 июня 2019
Категория:Математика
Содержит:10 слайд(ов)
Поделись с друзьями:
Скачать презентацию