Презентация "Приёмы устного решения квадратного уравнения" по математике – проект, доклад
Презентацию на тему "Приёмы устного решения квадратного уравнения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 28 слайд(ов).
Слайды презентации
Список похожих презентаций
Показательные уравнения, методы их решения
Что же такое показательные уравнения ? Показательные уравнения – это уравнения, в которых неизвестное число находится в показателе степени. Чаще всего ...Приёмы решения заданий
Определение времени часового пояса. Международные часовые пояса на территории России преобразованы в национальные часовые зоны. Для определения времени ...Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлена на множители
Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной. Содержание. Квадратный ...Понятие квадратного уравнения
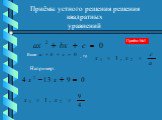
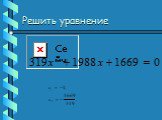
определение. Уравнение вида ах2+вх+с=0, где а,в,с – числа, а≠0, называется квадратным. Какие из уравнений являются квадратными. 1. 2х2+7х-3=0 2. 5х-7=0 ...Определение квадратного уравнения. Неполные квадратные уравнения
Тема урока: «Определение квадратного уравнения. Неполные квадратные уравнения» Цели урока: - познакомить учащихся с квадратными уравнениями в общем ...Определение квадратного уравнения. Неполные квадратные уравнения.
Эпиграф: Чтобы решить уравненье, Корни его отыскать, Нужно немного терпенья, Ручку, перо и тетрадь. Этапы подготовки:. Разбились на группы, которые ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0.1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...
Определение квадратного уравнения. Неполные квадратные уравнения
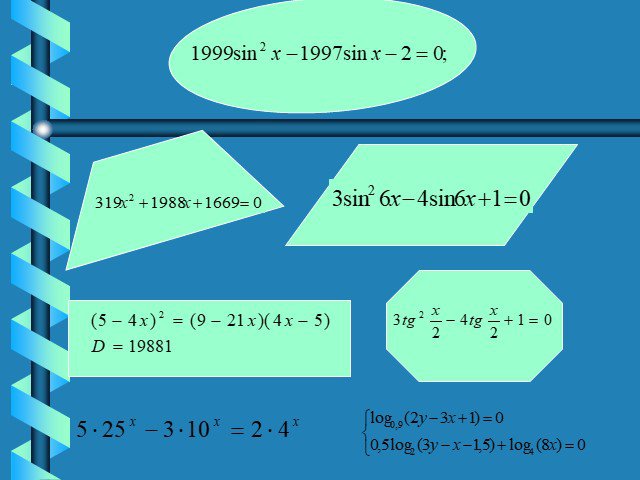
Решите уравнения Х=±2 Х=± Корней нет Х=0 Х=0,Х=2. 5х-2=0. Разделите данные уравнения на две группы. Какие уравнения называются квадратными? 1. Уравнение ...Нестандартные приёмы решения квадратных уравнений
Перечень тем сообщений. Как решали квадратные уравнения в древности. Общие методы решения квадратных уравнений. Специальные методы решения квадратных ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0. 1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...7 способов решения тригонометрического уравнения
Математики видят ее в:. гармонии чисел и форм, геометрической выразительности, стройности математических формул, решении задач различными способами, ...Как найти корни квадратного уравнения?
Привет, восьмиклассник! Твоему вниманию предоставляется проект, который поможет тебе научиться находить корни, квадратных уравнений. Здесь ты найдёшь ...Приёмы решения квадратных уравнений
История развития квадратных уравнений. Квадратные уравнения в Древнем Вавилоне. Необходимость решать уравнения не только первой, но и второй степени ...Показательные уравнения и способы их решения
Определение: Показательные уравнения – уравнения, в которых переменная входит только в показатели степеней при постоянных основаниях. Например,. Основные ...Поиски различных способов решения планиметрической задачи
РЕШИМ ЗАДАЧУ РАЗНЫМИ СПОСОБАМИ. Задача. В КМР на стороне КР взята точка А так, что КА:АР=1:3, а на стороне РМ–точка В, так, что РВ:ВМ=4:1, причём ...Неравенства и их решения
Неравенство Решить неравенство. Совокупность неравенств. Неравенства Алгебраические Трансцендентные рациональные иррациональные. Пример: Решить неравенство ...Методы решения уравнений
Результат учения равен произведению способности на старательность. Если старательность равна нулю, то и все произведение равно нулю. А способности ...Методы решения систем линейных уравнений 1- ой степени
Проверка домашнего задания. Устная работа. Какие способы решения систем линейных уравнений мы знаем? Сколько их? Какой из способов самый наглядный? ...Методы решения иррациональных уравнений
Из последнего промежутка найти наименьшее положительное целое число. I Y= II Y= III Y= IV Y= X ≥ 6 X > 0 X > -2 X ≥ 0. Найти область определения. ...Примеры решения тригонометрических уравнений
Примеры решения тригонометрических уравнений. Проверочная работа В заданиях 1-6 найдите значения аркфункций в заданиях 7-15 запишите решения простейших ...Конспекты
Определение квадратного уравнения. Неполные квадратные уравнения
План-конспект. урока по математике в 8 классе. «Определение квадратного уравнения. Неполные квадратные уравнения». Составила учитель ...Квадратные уравнения. Виды и способы решения
Тема: . Квадратные уравнения. Виды и способы решения. (Урок путешествие). Подготовила: Фисенко Т.В. - учитель математики МБОУ «СОШ № 92», г. Кемерово. ...Логарифмические уравнения и способы их решения
. План-конспект урока по теме:. «Логарифмические уравнения и способы их решения» (10 кл.). Автор:. Филиппова Е.М.,. учитель МБОУ СОШ №1. ...Определение квадратного уравнения. Неполные квадратные уравнения
ПЛАН-КОНСПЕКТ УРОКА «Определение квадратного уравнения. Неполные квадратные уравнения». . . ФИО (полностью). . Перькова Ирина Васильевна. ...Показательные уравнения и неравенства
. КГУ "Средняя школа №11 отдела образования акимата г. Тараз". Открытый урок. «Показательные уравнения и неравенства». . Класс. : ...Приёмы вычислений для случаев вида 26+7
Тема урока:. Приёмы вычислений для случаев вида 26+7. Тип урока:. изучение нового материала и первичного закрепления. Цель:. познакомить с ...Нестандартные способы решения уравнений
Муниципальное общеобразовательное учреждение. Шенталинская средняя общеобразовательная школа № 1 «Образовательный центр» муниципального района Шенталинский ...Биквадратные уравнения
Иванова Ольга Александровна. МОУ «СОШ №2» г. Всеволожска. Учитель математики. Урок по теме: «Биквадратные уравнения». Цели урока:. . Обучающие:. ...Методы решения показательных уравнений
План-конспект урока обобщающего повторения. . «Методы решения показательных уравнений». Цели урока:. Обобщение знаний и умений учащихся по ...Нелинейные уравнения с двумя переменными
Тема урока: Нелинейные уравнения с двумя переменными. Цели урока:. - обучить учащихся решению системы нелинейных уравнений с двумя переменными;. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Бойко Т.А.
Содержит:28 слайд(ов)
Поделись с друзьями:
Скачать презентацию