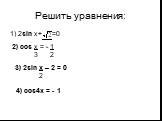Презентация "Решение простейших тригонометрических уравнений (2-й час)" по математике – проект, доклад
Презентацию на тему "Решение простейших тригонометрических уравнений (2-й час)" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
8 класс "Решение квадратных уравнений"
. . . . . . «Уравнение – это золотой ключ, открывающий все математические тайны». . Цель: привести в систему знания о квадратных уравнениях и умение ...меню для тригонометрических уравнений
Используемая литература. Алимов Ш.А. Алгебра и начала анализа 10-11 класс / Москва «Просвещение» 2002 год Тырымов А. А. методические пособия по математике ...Методы решений тригонометрических уравнений
Цели урока:. Рассмотреть тригонометрические уравнения, решаемые с помощью: понижения степени введения вспомогательного угла и др. Разминка. Arcsin(a), ...Итоговый урок: решение систем уравнений
ЦЕЛИ УРОКА. 1. повторить определения понятий: -система уравнений; -решение систем уравнений; -способы решения систем уравнений. 2. Найти практическое ...Решение диофантовых уравнений
Цели и задачи. Биография Диофанта Диофантовы уравнения с одной неизвестной Диофантовые уравнения первой степени Диофантовые уравнения высших степеней ...Методы решения тригонометрических уравнений
ЦЕЛЬ:.Систематизировать, обобщить, расширить знания и умения, связанные с применением методов решения тригонометрических уравнений. . . 1. Какие ...
Исследование жизненных ситуаций с помощью классического определения вероятности и решение простейших задач
Цель – научить учащихся вычислять вероятности в задачах, описывающих жизненные ситуации Задачи : знакомство с языком теории вероятностей; рассмотрение ...Методы решения тригонометрических уравнений
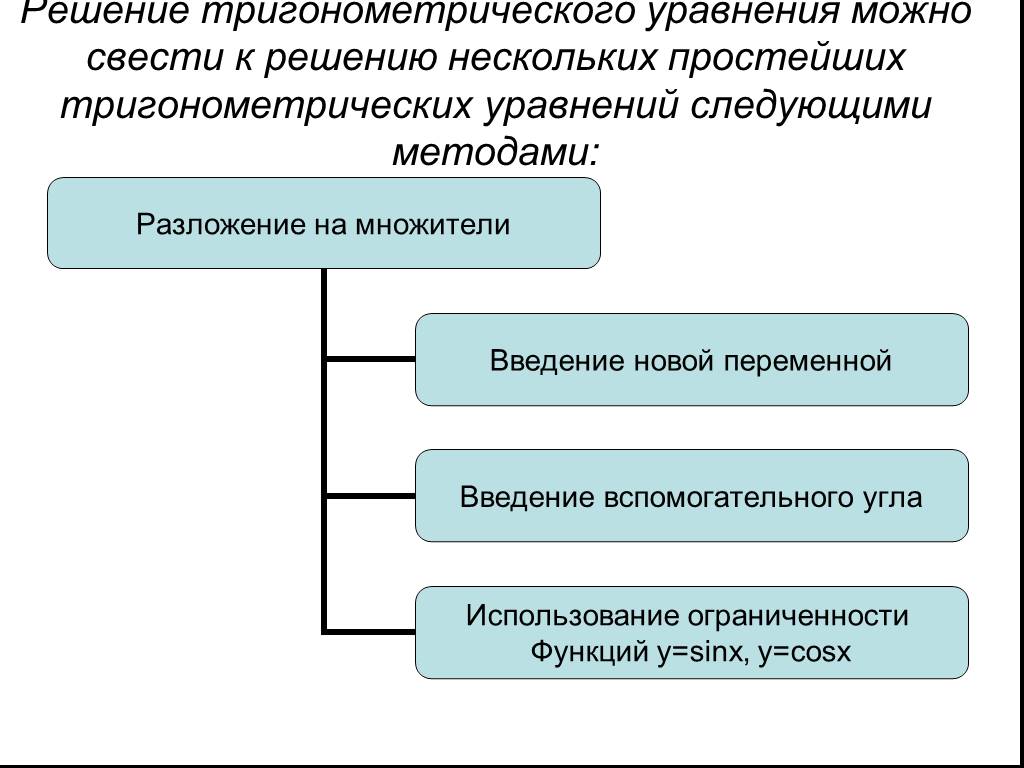
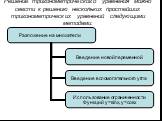
Восемь способов решения одного тригонометрического уравнения. 1.Приведение уравнения к однородному. 2.Разложение левой части уравнения на множители. ...Методы решения тригонометрических уравнений
«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию». Я. А. Коменский. Арксинус. ...Графическое решение уравнений
Установите соответствие:. А) парабола Б) ветвь параболы С) «галочка» Д) прямая. 4, 6 9 3. х у 0 1 х = 0. х = 0, х = 1. х = -2, 6 0 2 3 4 -2 6. . -2 ...Методы решения тригонометрических уравнений
«Думай о смысле, а слова придут сами». Льюис Кэрролл. Методы решения тригонометрических уравнений Указать метод решения уравнения:. . . . . . Методы ...Графическое решение систем уравнений
Правило решения системы уравнений графическим способом. Построить графики каждого из уравнений системы. Найти координаты точки пересечения построенных ...Графическое решение уравнений
АЛГЕБРА– 7 КЛАСС. ТЕМА: Графическое решение уравнений. Проверка домашнего задания. № 973 № 974. № 976 (а) построить функцию у = х2, построить функцию ...Графическое решение квадратных уравнений
Цель урока. формировать умение решать квадратные уравнения графическим способом. Решить уравнение х2 – 2х –3 = 0. Решение. I способ Построим график ...Графическое решение систем уравнений
Лаборатория «ТРУД». Твори, Решай, Учись, Добивайся с интересом и удовольствием! Руководители лаборатории. Начальник лаборатории: Ноумэн Ноу Мэнович ...Графическое решение квадратных уравнений
Немного истории. Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений. Диофант Александрийский, Аль- Хорезми . Евклид Омар Хайям. ...Ох уж эти показательные… Решение показательных уравнений и неравенств
Ответьте на вопросы. 1. Какая функция называется показательной? 2. Какова область определения показательной функции? 3. Какова область значений показательной ...Примеры решения тригонометрических уравнений
Примеры решения тригонометрических уравнений. Проверочная работа В заданиях 1-6 найдите значения аркфункций в заданиях 7-15 запишите решения простейших ...Методы решения тригонометрических уравнений
«Счастливый случай». 1 гейм «Разминка». 1. Решение уравнения вида cos x=a при |a| > 1? 2. При каком значении а, уравнение cos x =a имеет решения? ...Объем прямоугольного параллелепипеда. Решение задач
Объем прямоугольного параллелепипеда. Решение задач. ABCDA1B1C1D1–прямоугольный параллелепипед. а) V = a²h б) V = 1/2d²b в) V = abc г) V = 1/2d²bsinφ. ...Конспекты
Методическая разработка Урок математики в 6 классе Решение уравнений (урок закрепления)
Муниципальное образовательное учреждение. Средняя общеобразовательная школа №40 п.г.т. Шерловая Гора. Методическая разработка. Урок математики ...Методы решение показательных уравнений
Автор: Дементьева Ирина Николаевна. Место работы: МБОУ СОШ №2. с.Кривополянье Чаплыгинского района. Липецкой области. . Должность: учитель ...Логарифмы и решение логарифмических уравнений
Ибрагимов Рустем Фаткулкадирович. учитель математики. МБОУ «Русско-татарская общеобразовательная средняя школа №81». Урок алгебры и начала ...Примеры решения тригонометрических уравнений
Урок алгебры в 10-м классе. Тема: «Примеры решения тригонометрических уравнений». Олей Вера Ивановна. учитель математики. Разделы:. . Преподавание ...Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений
Тема:. «Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений». Тип урока:. урок изучения нового материала. Цели урока:. ...Логарифмы и решение логарифмических уравнений
Кукса Людмила Сергеевна. учитель математики. МБОУСОШ № 3 Ленинградского района Краснодарского края. Урок алгебры и начала анализа по теме. ...Знакомство с уравнениями. Решение уравнений методом подбора
Урок математики во 2 классе. Тема: Знакомство с уравнениями. Решение уравнений методом подбора. Цели урока:. . Обучающие:. открыть вместе ...Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений
Тема урока: Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений. Цели урока:. Образовательные. :. . ...Общие методы решения тригонометрических уравнений
. ГБОУ ООШ с. Малое Ибряйкино. Похвистневского района Самарской области. Конспект урока для 10 класса на тему. «Общие методы ...Основные методы решения тригонометрических уравнений
. МАТЕМАТИКА 11 класс. Тема: Основные методы решения тригонометрических уравнений. Цели урока:. Обобщить и систематизировать полученные знания ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:2 мая 2019
Категория:Математика
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию