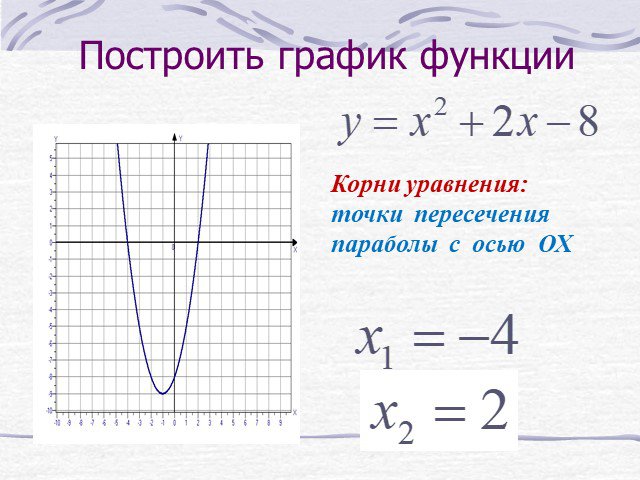
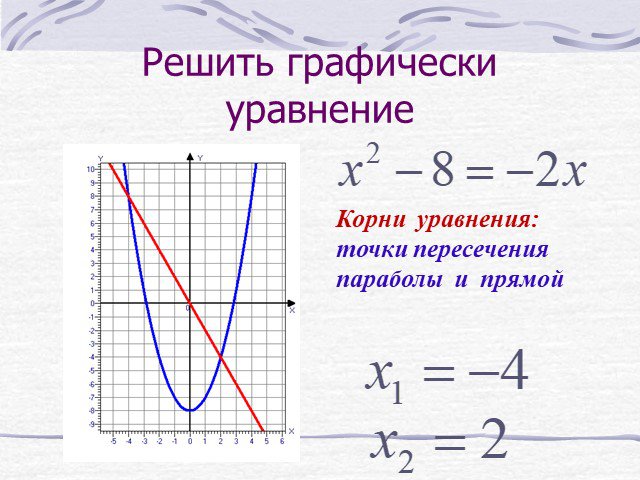
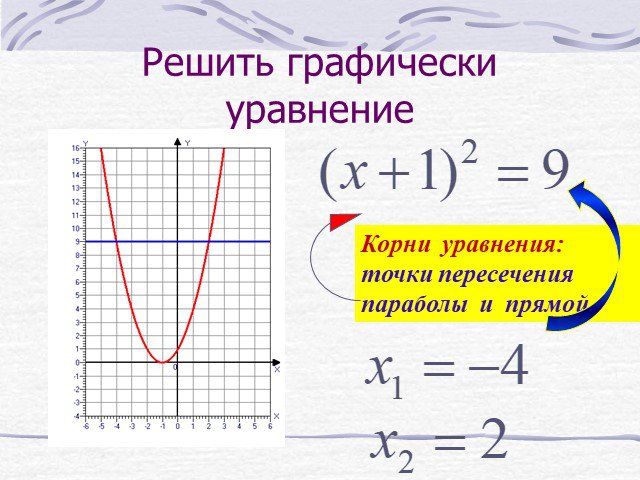
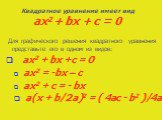Презентация "Графическое решение квадратных уравнений" (8 класс) по математике – проект, доклад
Презентацию на тему "Графическое решение квадратных уравнений" (8 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 38 слайд(ов).
Слайды презентации
Список похожих презентаций
Графическое решение квадратных уравнений
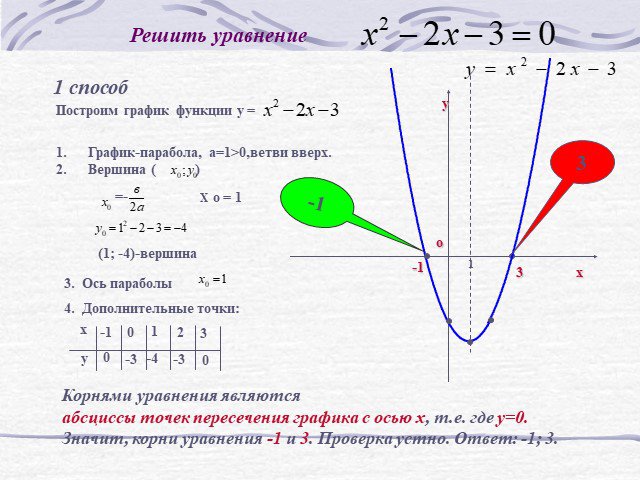
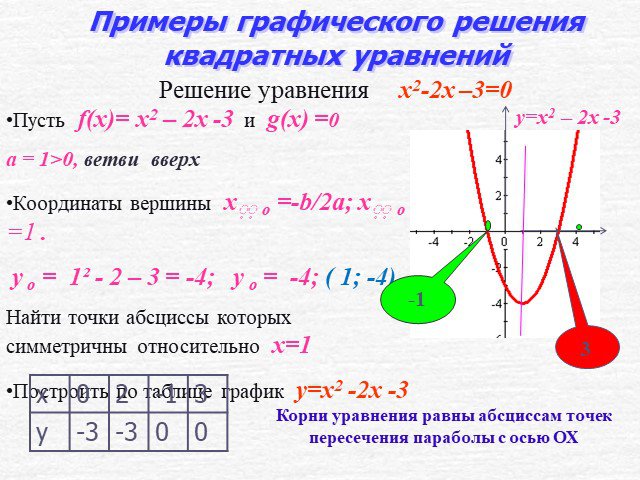
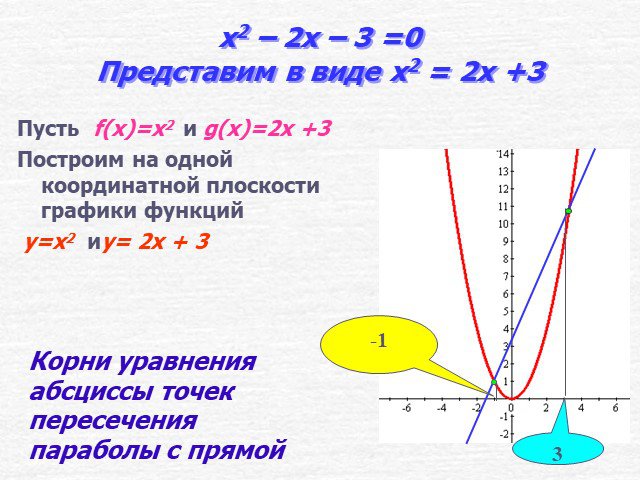
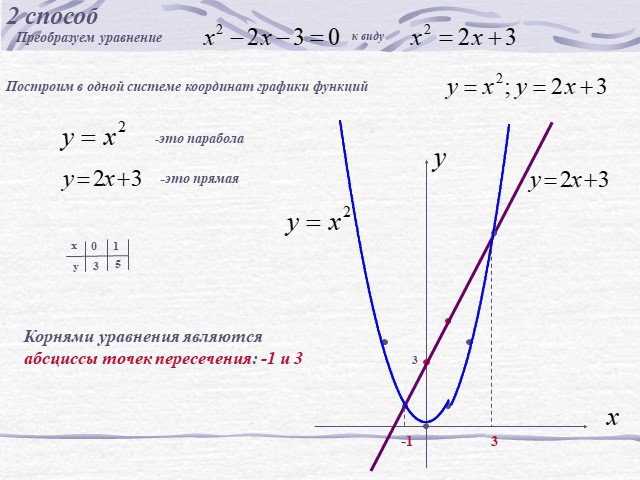
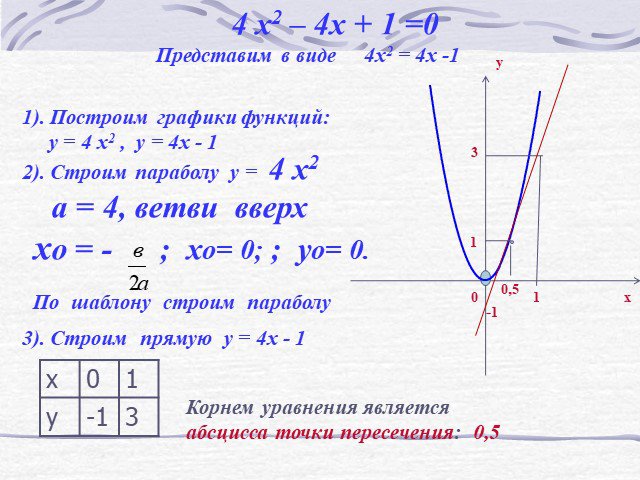
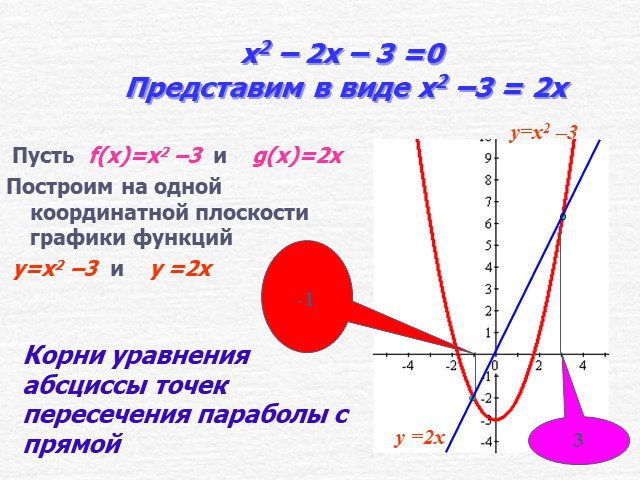
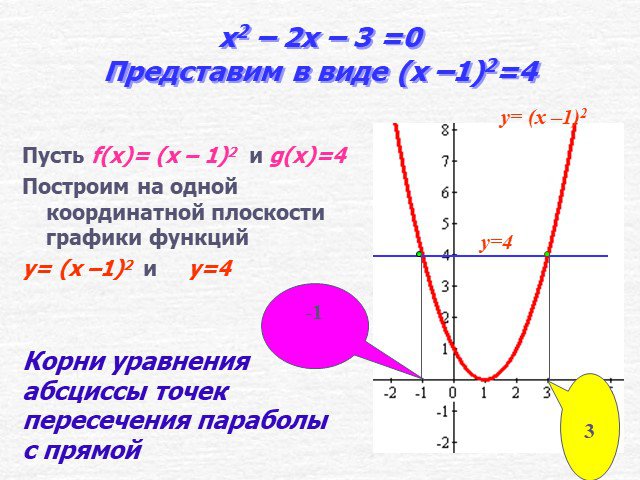
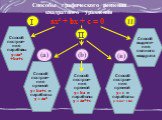
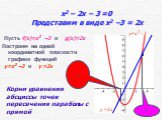
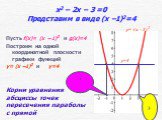
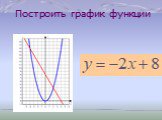
Цель урока. формировать умение решать квадратные уравнения графическим способом. Решить уравнение х2 – 2х –3 = 0. Решение. I способ Построим график ...Графическое решение систем уравнений
Правило решения системы уравнений графическим способом. Построить графики каждого из уравнений системы. Найти координаты точки пересечения построенных ...Графическое решение систем уравнений
Лаборатория «ТРУД». Твори, Решай, Учись, Добивайся с интересом и удовольствием! Руководители лаборатории. Начальник лаборатории: Ноумэн Ноу Мэнович ...Графическое решение уравнений
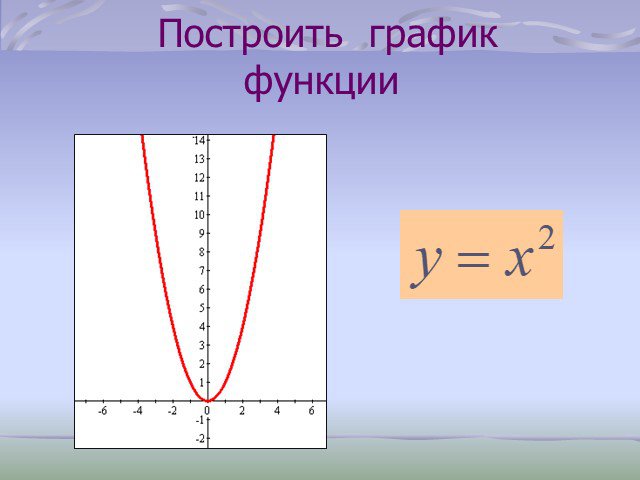
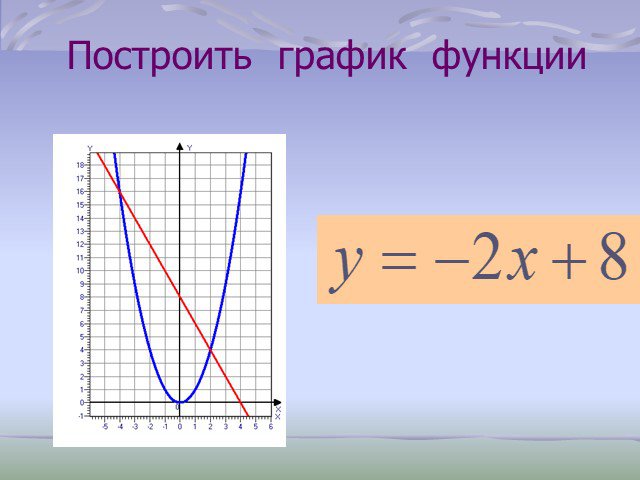
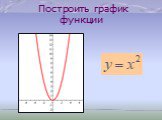
АЛГЕБРА– 7 КЛАСС. ТЕМА: Графическое решение уравнений. Проверка домашнего задания. № 973 № 974. № 976 (а) построить функцию у = х2, построить функцию ...Графическое решение уравнений
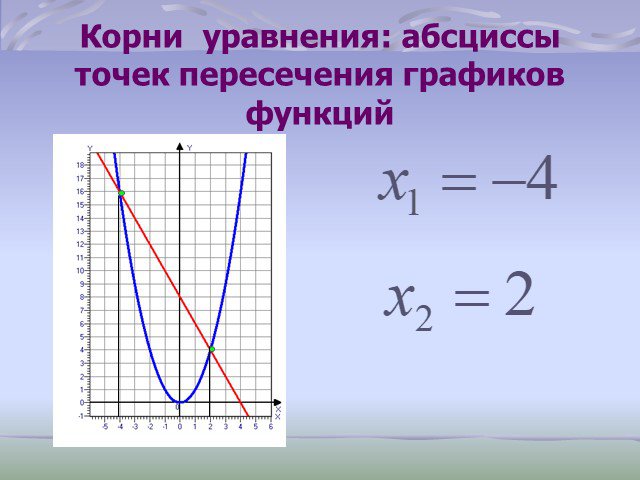
Установите соответствие:. А) парабола Б) ветвь параболы С) «галочка» Д) прямая. 4, 6 9 3. х у 0 1 х = 0. х = 0, х = 1. х = -2, 6 0 2 3 4 -2 6. . -2 ...8 класс "Решение квадратных уравнений"
. . . . . . «Уравнение – это золотой ключ, открывающий все математические тайны». . Цель: привести в систему знания о квадратных уравнениях и умение ...В мире квадратных уравнений
Оглавление. Введение Заметки прошлого Основные понятия Теорема Виета Способы решения квадратного уравнения. Математика — основа точных наук. На первый ...Решение диофантовых уравнений
Цели и задачи. Биография Диофанта Диофантовы уравнения с одной неизвестной Диофантовые уравнения первой степени Диофантовые уравнения высших степеней ...10 способов решения квадратных уравнений
История развития квадратных уравнений. Квадратные уравнения в Древнем Вавилоне: Х2+Х=3/4 Х2-Х=14,5. Как составлял и решал Диофант квадратные уравнения. ...Виды квадратных уравнений
гипотеза. Каждый человек, особенно если он ученик 8 класса, может решить квадратное уравнение, если знает ответы на вопросы…. вопросы... Определение ...Итоговый урок: решение систем уравнений
ЦЕЛИ УРОКА. 1. повторить определения понятий: -система уравнений; -решение систем уравнений; -способы решения систем уравнений. 2. Найти практическое ...Общие методы решения квадратных уравнений
При решении квадратных уравнений часто применяется метод разложения на множители (с помощью вынесения за скобки общего множителя, формул сокращенного ...Нестандартные приёмы решения квадратных уравнений
Перечень тем сообщений. Как решали квадратные уравнения в древности. Общие методы решения квадратных уравнений. Специальные методы решения квадратных ...Ох уж эти показательные… Решение показательных уравнений и неравенств
Ответьте на вопросы. 1. Какая функция называется показательной? 2. Какова область определения показательной функции? 3. Какова область значений показательной ...история квадратных уравнений
Цель:. •Познакомить учащихся с учеными математики, открытия которых являются основой научно-технического прогресса. •Наглядно продемонстрировать применение ...Новое свойство квадратных уравнений
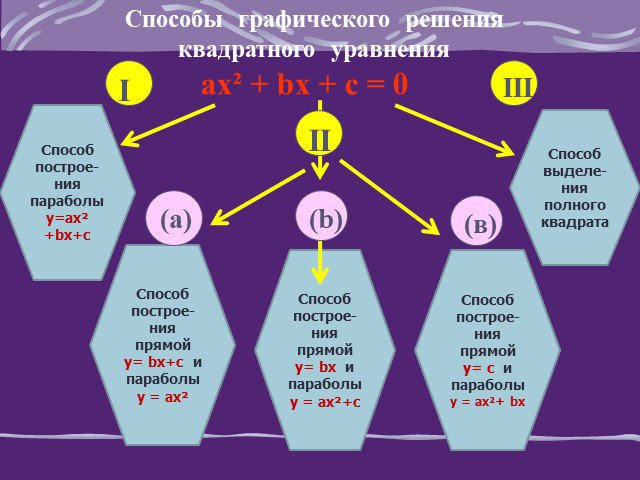
Вы решали квадратные уравнения различными способами: выделением квадрата двучлена, по формуле корней, с помощью теоремы Виета, и каждый раз убеждались ...Пять графических способов решения квадратных уравнений
Цель урока:. Применение навыков построения графиков функций при решении квадратных уравнений. План урока. Актуализация знаний. Новый материал: 5 способов ...Методы решения квадратных уравнений
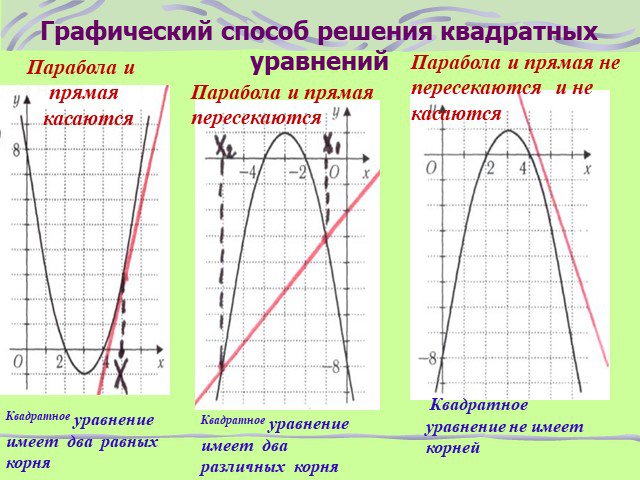
Определение. Квадратные уравнения (КВУР) – уравнения вида ax²+bx+c=0, где x – переменная, a, b и c – любые числа, причем a≠0. (В случае, когда а = ...Графический способ решения квадратных уравнений
Графический способ решения уравнений. Решить графически уравнение. Ответ: х=-3 или х=1. Самостоятельная работа. 1. Постройте график функции и укажите ...Различные способы решения квадратных уравнений
Человеку, изучающему алгебру, часто полезнее решить одну задачу тремя различными способами, чем решать три-четыре различные задачи. Решая одну задачу ...Конспекты
Графическое решение квадратных уравнений
МБОУ «Гимназия №3». Конспект урока по математике в 8 классе на тему:. Учитель математики 1 кв.категории:. . Назарова ...Графическое решение квадратных уравнений
Управление образования. администрации Павловского района. Проект урока. Предмет алгебра. класс 8 В. Тема. Графическое решение ...Графическое решение квадратных уравнений
Графическое решение квадратных уравнений. . Цели урока:. . закрепить основные методы и навыки техники построения и чтения графиков линейных ...Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений
Тема урока: Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений. Цели урока:. Образовательные. :. . ...Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений
Тема:. «Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений». Тип урока:. урок изучения нового материала. Цели урока:. ...Решение биквадратных уравнений
МУНИЦИПАЛЬНОЕ ОБРАЗОВАНИЕ ТАЗОВСКИЙ РАЙОН. Муниципальное казенное общеобразовательное учреждение. Тазовская школа – интернат среднего (полного) ...Решение дробных рациональных уравнений
Муниципальное бюджетное общеобразовательное учреждение. «Новомихайловская средняя общеобразовательная школа». Татарского района Новосибирской области. ...Решение задач и уравнений
«Решение задач и уравнений». Тип урока:. нестандартный. Класс:. 3. Тема урока:. Закрепление решение задач и уравнений. Цель урока:. закрепление ...Рациональные способы решения квадратных уравнений
ПРОБЛЕМНОЕ ОБУЧЕНИЕ. РАЗВИТИЕ ПОЗНАВАТЕЛЬНЫХ СПОСОБНОСТЕЙ. В ходе урока учащиеся знакомятся с нестандартными (не входящими в программу) способами ...Решение дробных рациональных уравнений
«. Решение дробно-рациональных уравнений». . Урок: алгебра 9 класс. Тема. :. . Решение дробных рациональных уравнений. Цель:. . познакомить ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 апреля 2015
Категория:Математика
Классы:
Содержит:38 слайд(ов)
Поделись с друзьями:
Скачать презентацию