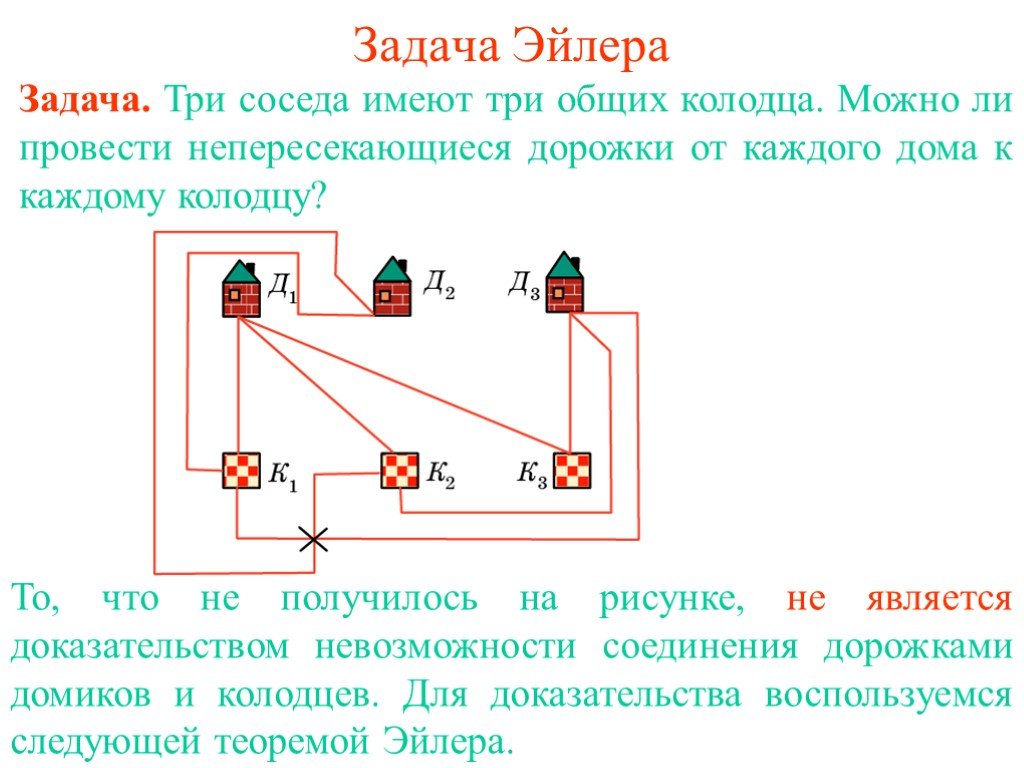
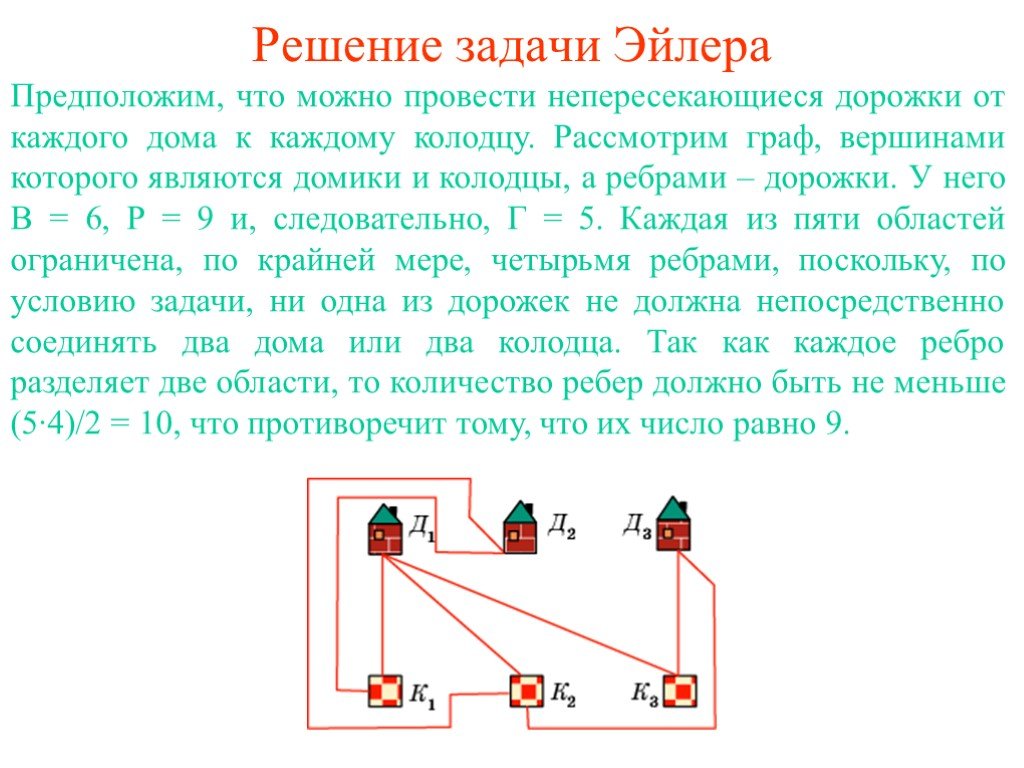
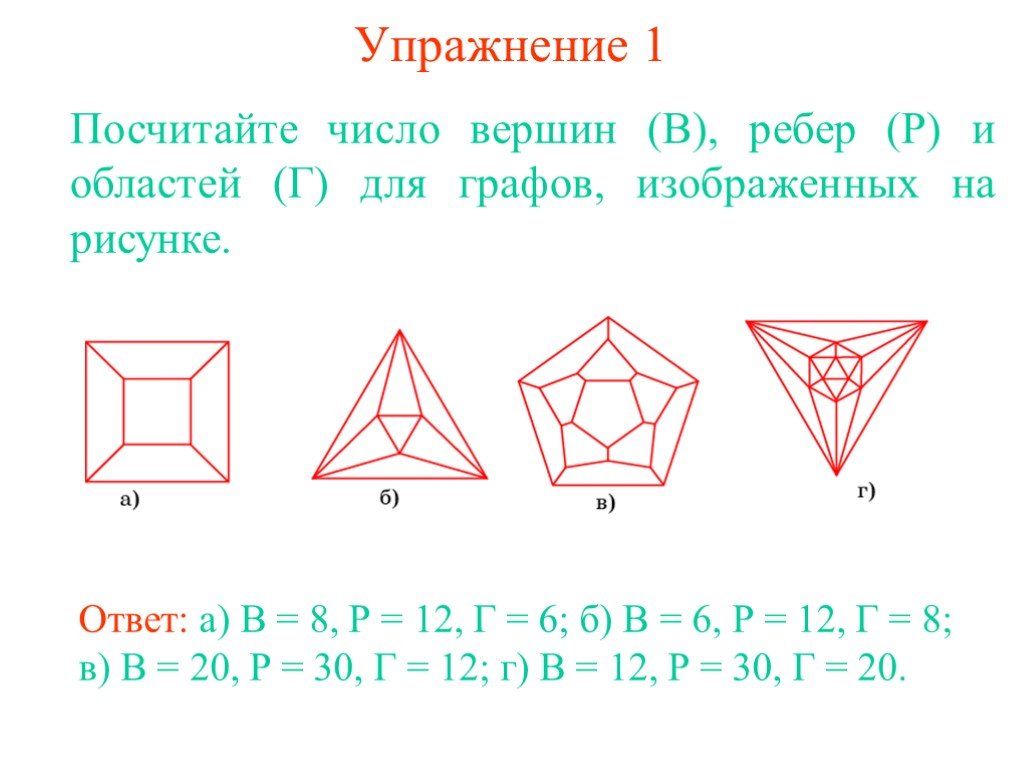
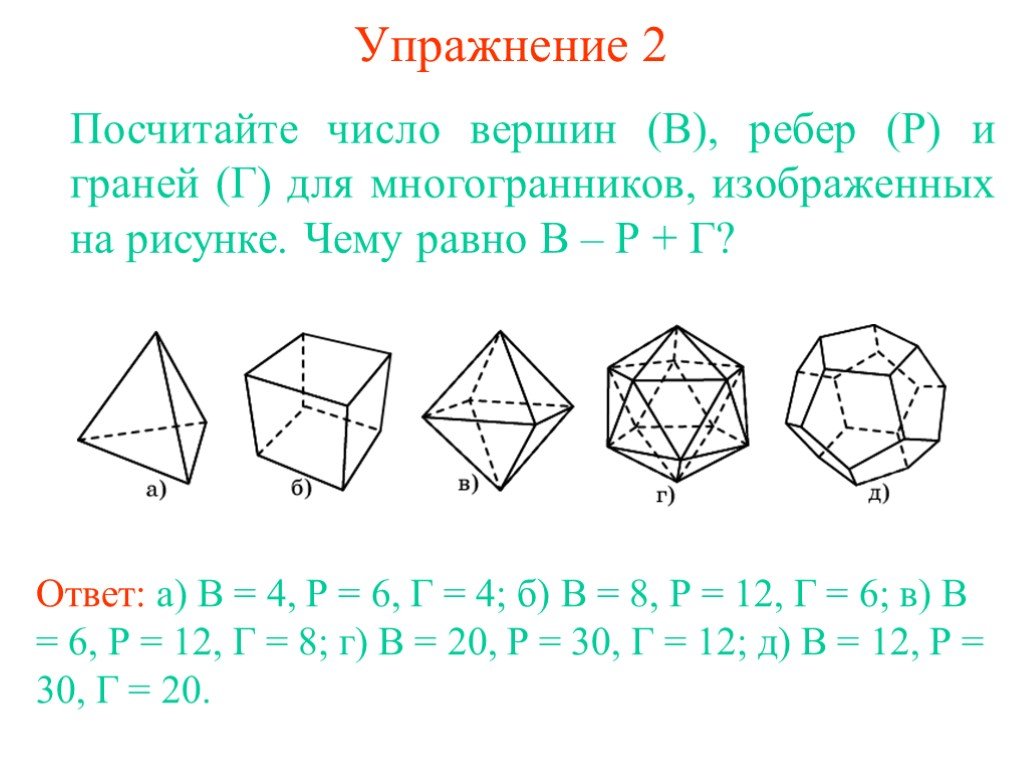
Презентация "Задача Эйлера" по математике – проект, доклад
Презентацию на тему "Задача Эйлера" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 9 слайд(ов).
Слайды презентации
Список похожих презентаций
Круги Эйлера
Цель исследования: изучение биографии Л. Эйлера изучение способа решения задач с помощью кругов Эйлера; Задачи исследования: Познакомится с кругами ...Круги Эйлера
Круги Эйлера. Один из величайших математиков петербургский академик, за свою долгую жизнь он написал более 850 научных работ. В одной из них появились ...Круги Эйлера
№1. Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги ...Круг Эйлера
Выполнила:. Жубанова Диана ученица 7 класса Карасаевской СОШ. Цель исследования: Изучить круги Эйлера Научиться применять данный способ для решения ...Круги Эйлера
Леонард Эйлер. Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал ...Задача №10
Верно ли, что прямая лежит в плоскости данного треугольника, если она: А) пересекает две стороны треугольника; Б) проходит через одну из вершин треугольника;. ...Знакомство с теоремой Эйлера
Теорема Эйлера- математическое утверждение, связывающее между собой число ребер, граней и вершин многогранников. Она хорошо известна и присутствует ...Задача о трисекции угла
Задача о трисекции угла разрешима при некоторых частных значениях величины данного угла. A C N M B D. При помощи циркуля и линейки можно разделить ...Задача Пуассона
Задача Пуассона. Некто имеет двенадцать пинт вина (ПИНТА- старинная мера жидкости, равная примерно 0,568л.) и хочет подарить из него половину, но ...Задача и пять методов её решения
Введение. Для успешного изучения геометрии необходимо знать не только основные формулы и теоремы, но и владеть различными методами решения задач. ...Задача на увеличение числа
Цель: решение задач на увеличение числа Задачи: - помочь усвоить алгоритм решения задач на увеличение числа, ввести схему из отрезков для моделирования ...Задача для знатоков монет и математики
. Имеется 10 монет: 2 по 2 копейки, 2 по 3 копейки, два пятака, два гривенника, один пятиалтынный и один двугривенный. Разместите их в кружках звезды ...Задача Дидоны
Содержание. Введение. Цели, задачи, актуальность. Введение. Миф о Дидоне. Практическая часть. Способы решения изопериметрической проблемы. Первый ...Задача В-9 ЕГЭ. Многогранники
Условие. Найдите угол ЕАД2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Построим треугольник ...Открытый банк заданий по математике Задача №14
Каким уравнением задается прямая, проходящая через точки A(2; -5) и B(14; 1) ? Задание 14 (№ 206198) Подсказка 3 4 1. Необходимо значения координат ...Замысловатые маршруты Эйлера
Кенигсбергские мосты А, В, С, D – части континента, отделённые друг от друга а, b, с, d, e, f, g – мосты А, В, С, D – узлы(вершины) а, b, с, d, e, ...Решение логических задач с помощью кругов Эйлера
Из 90 туристов, отправляющихся в путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Решение: Покажем условие задачи ...Теорема Эйлера и ее применение
ТЕОРЕМА ЭЙЛЕРА. Из приведенной таблицы непосредственно видно, что для всех выбранных многогранников имеет место равенство В - Р + Г = 2. Оказывается, ...Задача
"Повторять да учить - ум точить". . 6, 10, 5, 7,4. 4, 5, 6, 7, 10. По форме 5 и 5 По цвету 6 и 4 По размеру 8 и 2. 10. 9 и 1 8 и 2 7 и 3 6 и 4 5 и ...Фракталы – геометрия природы
Задачи:. узнать, что такое «фракталы»; изучить историю возникновения и развития фрактальной геометрии; ознакомиться с биографией создателя фракталов ...Конспекты
Задача +3, -3
Учитель: Корецкая Светлана Николаевна. Предмет:. Математика. Тема:. Задача +3,-3. Цель:. . Развить знания учащихся о задачах на нахождение ...Задача на движение
Задача на движение. 19,5 км/ч 25,4 км/ч. . . ? . . 3 ч. . 3 ч. . 220 км. Задача на движение. 60 км/ч на 15,1 км/ч. . > . ...Задача (Столько же) Сложение и вычитание (6+0, 7+3, 9-1, 10-3) Самостоятельная работа
Глущенко Елена Владимировна – учитель начальных классов второй квалификационной категории. КГУ «Средняя школа №5» г. Петропавловск, Северо-. Казахстанская ...Задача (условие, вопрос)
Проект урока. Фамилия, имя отчество. Дзюбак Наталья Николаевна. Место работы (полное название ОУ). МБОУ «Кусакская СОШ» ННР Алтайского края. Используемый ...Задача – основное математическое понятие
Автор: Лактюшина СветланаЛеонидовна , учитель начальных классов. МБОШИ «Технический лицей-интернат № 128», город Новосибирск, Первомайский район. ...Задача – это…
Открытый урок по математике. . «Задача – это…». (1 класс; УМК «Перспективная начальная школа»). Учитель начальных классов. высшей квалификационной ...Задача
Конспект урока по математике. Место работы: Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная. школа № 7. . ...Задача
Урок математики в 1 классе. . (по УМК «Перспектива», учебник «Математика» 1 класс, автор Л.Г.Петерсон). Тема: Задача. Цели урока:. 1) тренировать ...Задача
Муниципальное бюджетное образовательное учреждение. «Основная общеобразовательная школа ст. Миннибаево» Альметьевского муниципального района Республики ...Задача
Муниципальное бюджетное общеобразовательное учреждение. «Макуловская средняя общеобразовательная школа». Верхнеуслонского муниципального района. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 марта 2019
Категория:Математика
Содержит:9 слайд(ов)
Поделись с друзьями:
Скачать презентацию