Презентация "Иррациональные уравнения. Урок-дискуссия" (10 класс) по математике – проект, доклад
Презентацию на тему "Иррациональные уравнения. Урок-дискуссия" (10 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Иррациональные уравнения
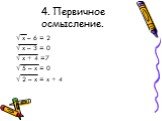
ПОНЯТИЕ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ. Если в уравнении переменная содержится под знаком квадратного корня, то уравнение называют иррациональным. ? Примеры:. ...Иррациональные уравнения
Цели урока. Ввести понятие иррациональных уравнений и показать способы их решения; Выработать умение мыслить, делать выводы, применять теоретические ...Иррациональные уравнения
Цель урока:. Обобщение и систематизация способов решения иррациональных уравнений. Развивать умение обобщать, правильно отбирать способы решения иррациональных ...Иррациональные уравнения
. Например:. Иррациональные уравнения содержат радикалы. Чтобы избавиться от радикалов, необходимо возвести обе части уравнения в одну и ту же степень ...Иррациональные уравнения
Домашнее задание:. Обязательное задание. Сложное задание. Задание повышенной сложности. «ХОД КОНЕМ» НИИ И НАЛЬ ШЕ ЕЮ ЗО У РЕА ИР ПОСТА НИЙ РЕ ДИ ЦИО ...Неполные квадратные уравнения
Устный счёт. а) Вычислить: 32 , (-2)2,. б) Решить уравнения, сколько корней они имеют? X2 = 4 x2= - 16 3x2 = 0 в) Разложить на множители: x2 - 4 2x2 ...Логарифмические уравнения и их системы
Функция y = loga х (где а > 0, а =1) называется логарифмческой. График логарифмической функции logaх можно построить, воспользовавшись тем, что функция ...Формула корней квадратного уравнения
Сегодня на уроке мы будем:. записывать квадратные уравнения; вспоминать формулы нахождения корней квадратного уравнения; решать квадратные уравнения ...Тригонометрические уравнения и методы их решения
«Великая книга природы открыта для нас, но научиться понимать ее можно лишь путем прилежания, любви, страданий. Язык этот-математика. Математика расцветает ...Решение уравнения sin t = a
Повторение 1. Вычислите: arccos( ). 2. Какое из выражений не имеет смысла? 3. Решите уравнение: cost=½. v. Самостоятельная работа. 1. Вычислите: а) ...Арксинус. Решение уравнения sin t = a
Цели. Изучить определение арксинуса числа. Изучить формулы решения простейшего тригонометрического уравнения sin t = a. Повторим. Что называется синусом ...График линейного уравнения с двумя переменными
Закончите предложение:. Линейным уравнением с двумя переменными называется уравнение вида. ах+by=с, где х и y – переменные, а, b и с – некоторые числа. ...Диофантовы уравнения
Цели и задачи. Определение диофантова уравнения Биография Диофанта Диофантовые уравнения первой степени Диофантовые уравнения высших степеней Проект ...Диофантовы уравнения
СКОЛЬКО РЕШЕНИЙ ИМЕЕТ ДАННОЕ УРАВНЕНИЕ? (2х+у)(5х+3у)=7. 3) Не имеет решений. 4) Бесконечно много решений. Следующее задание. (3х+7у)(х-у)=13 1) 2 ...Диофантовы уравнения
Диофантовы уравнения Глобально не изучаются в школьной программе, а присутствуют на экзамене! Проблема подтолкнувшая на создание работы:. обусловлена ...Диофантовы уравнения
Цели учебно – исследовательской работы: изучить способы решения диофантовых уравнений; повысить уровень математической культуры, прививая навыки самостоятельной ...Графическое решение линейного уравнения с двумя переменными
Цель урока:. проверить прочность знаний, умений и навыков, учащихся по данной теме, обеспечить закрепление и обобщение изученного материала; развивать ...Графики линейного уравнения с двумя переменными
Цель урока:. ввести понятие графика уравнения с двумя переменными; повторить построение графика линейной функции по двум точкам; закрепить навыки ...Однородные тригонометрические уравнения
Кроссорд. 1. Значение переменной, обращающее уравнение в верное равенство 2. Единица измерения углов 3. Числовой множитель в произведении 4. Раздел ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0.1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...
Конспекты
Иррациональные уравнения. Метод замены переменной
Сунтарский улус (район). МБОУ «Аллагинская СОШ». . Открытый урок: Алгебра и начала математического анализа. Тема:. Иррациональные уравнения. ...Решение сложных иррациональных уравнений и систем, содержащих иррациональные уравнения
Болявина Наталья Сергеевна. Учитель математики. ГБОУ СОШ № 756 г. Москвы. Разработка урока по алгебре и началам анализа в 11 классе. ...Иррациональные уравнения
План – конспект урока. Обобщающий урок алгебры в 11 классе по теме:. «Иррациональные уравнения». Цель:. Обобщить знания по теме: «Иррациональные ...Иррациональные уравнения – просто и красиво
Тема урока. Обобщающий урок по теме. «Иррациональные уравнения – просто и красиво». Цели урока. : 1. образовательные. :. - повторить, обобщить ...Иррациональные уравнения
Муниципальное бюджетное общеобразовательное учреждение. Пролетарская средняя общеобразовательная школа №6 г. Пролетарска Пролетарского района Ростовской ...Иррациональные уравнения
Конспект урока в 11 классе по теме «Иррациональные уравнения». Три пути ведут к знанию:. путь размышления – это путь самый благородный,. . ...Иррациональные уравнения
Класс: 11. Предмет: математика. Тема урока:. Иррациональные уравнения. Цели урока:. . 1. . Ввести понятие иррациональных уравнений и показать ...Иррациональные уравнения
Урок по теме «Иррациональные уравнения». «Да, мир познания не гладок. И знаем мы со школьных лет. Загадок больше, чем разгадок. И поискам ...Иррациональные уравнения
Урок алгебры в 8 классе. Учитель: Габдукаева Физалия Каримовна. Тема урока: «Иррациональные уравнения». Цели:. Формирование навыков решения ...Иррациональные уравнения
ПЛАН-КОНСПЕКТ УРОКА Иррациональные уравнения. . ФИО (полностью). . Филимонова Лидия Михайловна. . . . Место работы. . МБОУ ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:4 октября 2018
Категория:Математика
Классы:
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию