Презентация "Это загадочное число Пи" по математике – проект, доклад
Презентацию на тему "Это загадочное число Пи" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 40 слайд(ов).
Слайды презентации
Список похожих презентаций
Загадочное число Пи
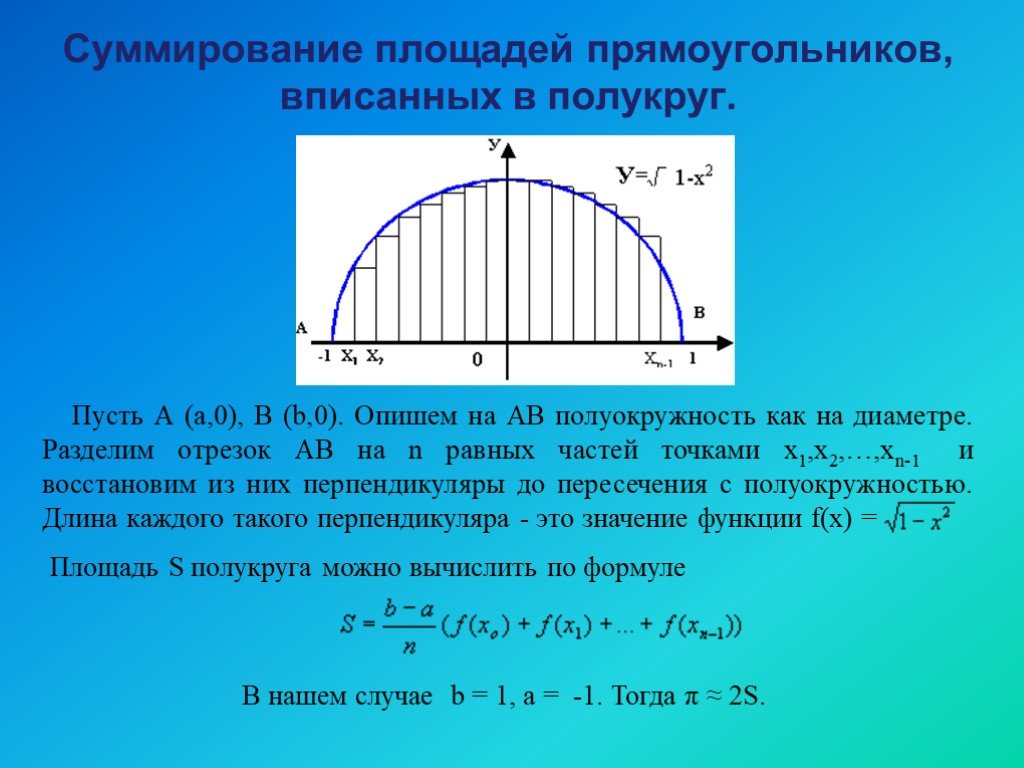
Пи, несомненно, одна из наиболее универсальных и фундаментальных констант, известных Человечеству. В силу своей универсальности Пи используется в ...Загадочное число ПИ
Цель:. Исследование природы числа ПИ и выявление его роли в окружающем нас мире. Задачи:. ситуации возникновения числа . трансцендентность числа ...Запись умножения на двузначное число столбиком
Чтоб водить корабли, Чтобы в небо взлететь, Надо многое знать, И при этом , и при этом, Вы заметьте-ка, Очень важная наука Ма-те-ма-ти-ка! Проверка ...Деление десятичной дроби на натуральное число
Это растение бергамот. Это цитрусовое растение. Плоды его несъедобны, но масло, которое получают из кожуры этих плодов, листьев и цветов, имеет приятный ...Неизвестное число в равенстве
Урок математики 4 класс. Тема: «Нахождение неизвестного числа в равенствах». Математику, друзья, Не любить никак нельзя. Очень точная наука, Очень ...Моё любимое число
Осваивать первичные методы исследования. Получить возможность применить имеющиеся знания и умения в реализации собственных интересов. Развивать интерес ...Математика число 4
17 декабря. Классная работа. . . ? Какие фигуры пропущены? 6 -2 -1 +2 +1. Найди ответ в конце цепочки. Сколько хвостиков у 9 осликов? Сколько лапок ...Как найти число, зная дробь
Цель урока:. обеспечить осознанное усвоение учащимися понятия нахождения части от числа и числа по его части за счет укрупнения дидактической единицы; ...Интересные факты о числе Пи
«Лицо π было скрыто маской. Все понимали, что сорвать её, не сможет никто…» Бертран Рассел. Хронология вычисления числа ПИ. Практические способы вычисления ...Изучаем число десять
Сказал весёлый круглый ноль Соседке - единице: - С тобою рядышком позволь Стоять мне на странице! Она окинула его Сердитым, гордым взглядом: - Ты, ...Деление на двузначное число
75:15 3 5. 45:15 4. 51:17 2. 70:35. 48:16 1. 60:15 6. 34: 17. 50:25. 64:16. 36:12. 52:13. 72:12 7. 84:14. 96:12 8. Здорово! http://dlm3.meta.ua/pic/0/51/193/P7K6KDqfij.jpg ...Деление на двузначное число
Математическая разминка. 32* 4. 720:6. 880:11. 560:14. . 810:27. Проверь 40 130 120 30. Определи, сколько цифр в частном. 2 123 856 : 36 45 846 : ...Деление на двузначное число
Вновь играя и шаля Перед носом корабля. Над водой мелькают спины, - Мчатся шустрые…. Деление на двузначное число. Чистописание. Прочитайте текст Выпишите ...Деление на двузначное число
1. 2014 Мобильная видео коммуникация. . Видео Емеил V-mail. 1. Конструктор видео сообщений и видео визиток 2. Функция записи видео сообщений 3. Автоматическая ...Деление на двузначное число
ПОТРЕНИРУЙСЯ! ...Деление на двузначное число
4 6 3 0. Первому неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого – ещё по одной цифре частного. 1 5 2. 8. 7 ...Деление десятичных дробей на натуральное число
Отрабатывать умения и навыки выполнения деления десятичной дроби на натуральное число; Развивать самостоятельность в деятельности; Развивать интерес ...Замечательные числа: число 6
Число 6. В нумерологии число 6 называют – гексада. Оно означает создание или сотворение чего-то нового и является символом симметрии и равновесия. ...Деление на двузначное число
Математику, друзья, Не любить никак нельзя. Очень тонкая наука, Очень строгая наука, Интересная наука- это математика! 1. Организационный момент. ...Деление на однозначное число двузначного с помощью разложения на разрядные слагаемые
. . . Дружба. . Тема: Деление на однозначное число двузначных чисел с помощью разложения на разрядные слагаемые. . . Физминутка. К морю быстро мы ...Конспекты
Письменное умножение на трёхзначное число
Урок математики 4 класс. Программа «Школа России», учебник Моро «Математика 4 класс». Голубева Наталья Викторовна учитель начальных классов. Тема:. ...Алгоритм письменного деления многозначного числа на двузначное, трёхзначное число
Открытый урок математики 4 класс. Тема: Алгоритм письменного деления многозначного числа на двузначное, трёхзначное число. Цель:. формирование ...Письменное умножение на двухзначное число
Муниципальное бюджетное образовательное учреждение. Гремячевская средняя общеобразовательная школа. Урок математики в 4 классе с презентацией. ...Письменное умножение на трехзначное число
Конспект урока. . по математике в 4 классе. по теме «Письменное умножение на трехзначное число». Выполнил:. . учитель начальных ...Письменное умножение на трёхзначное число
Математика 4 класс. Учитель: Жукова Елена Михайловна. Тема. : Письменное умножение на трёхзначное число. Цель урока. : сформировать у учащихся ...Письменное умножение на двузначное число
Математика - 4 класс, автор: М.И.Моро, «Школа России». Тип урока: ОНЗ. Тема: «Письменное умножение на двузначное число». Основные цели:. формирование ...Письменное умножение на двузначное число
Конспект. . урока математики в 4 классе «Письменное умножение. . на двузначное число». . учитель Филиппова Анна Викторовна. Тема урока: ...Письменное умножение на двузначное число
Муниципальное автономное общеобразовательное учреждение «Средняя общеобразовательная школа № 12 с углубленным изучением отдельных предметов» г. Губкин. ...Письменное умножение на двузначное число
Муниципальное общеобразовательное учреждение « Средняя общеобразовательная школа №2 с углубленным изучением иностранных языков» муниципального образования ...Письменное умножение многозначных чисел на однозначное число
Краевое государственное казенное специальное (коррекционное) образовательное учреждение. . для обучающихся, воспитанников с ограниченными возможностями ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 ноября 2018
Категория:Математика
Содержит:40 слайд(ов)
Поделись с друзьями:
Скачать презентацию