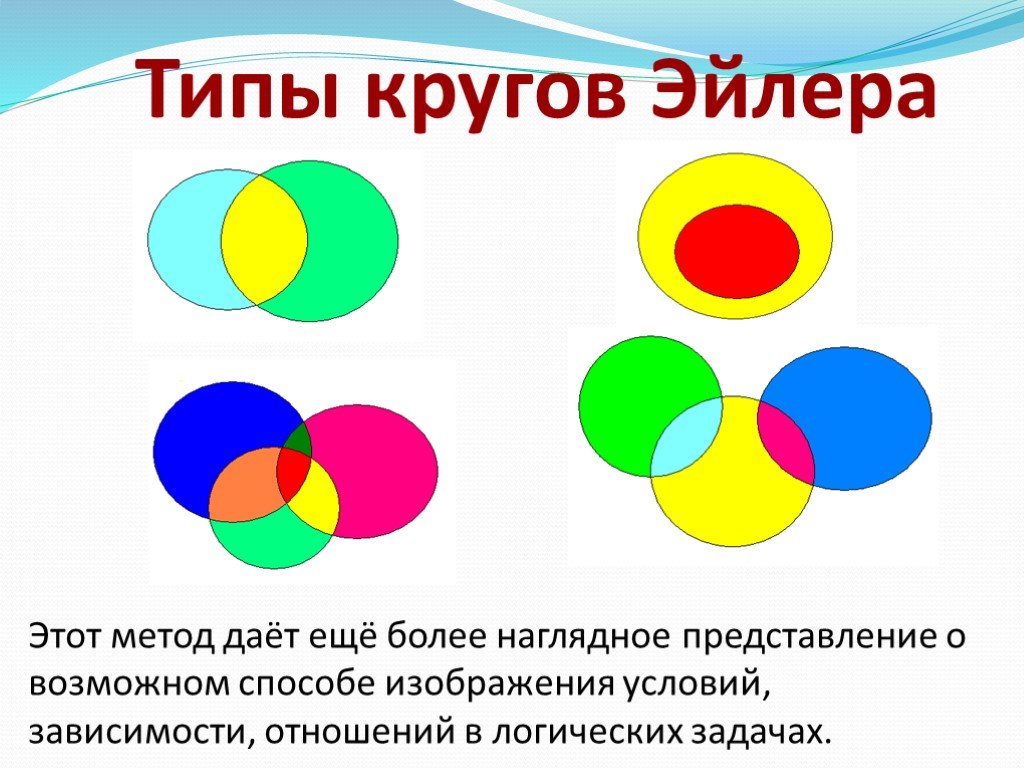
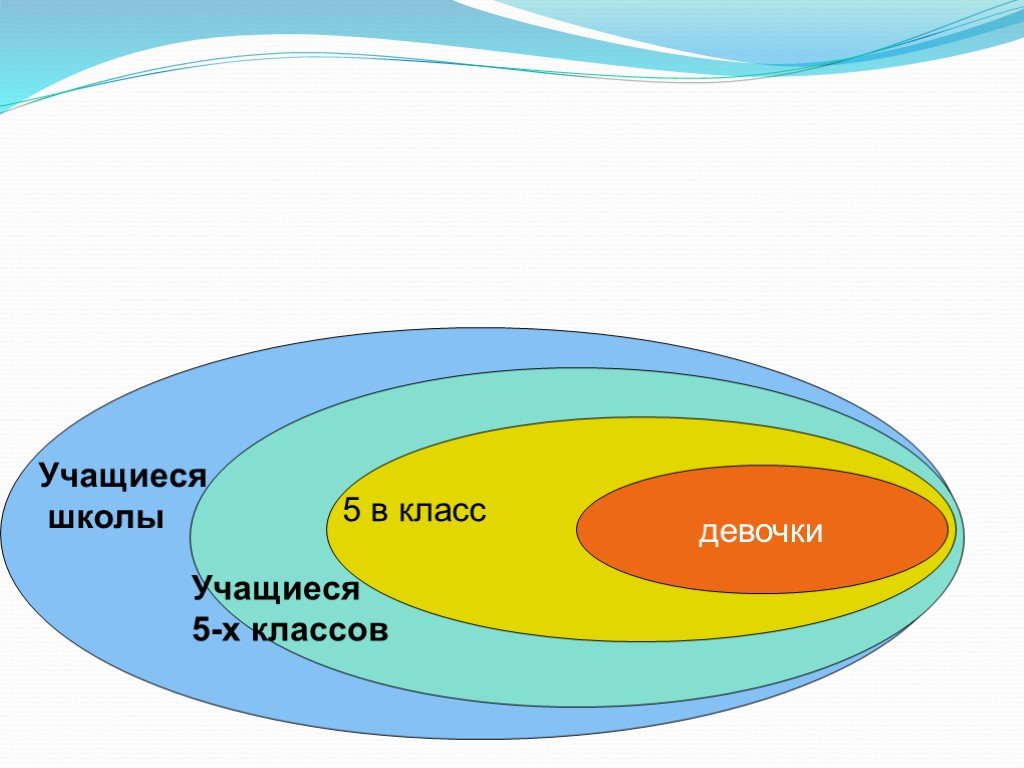
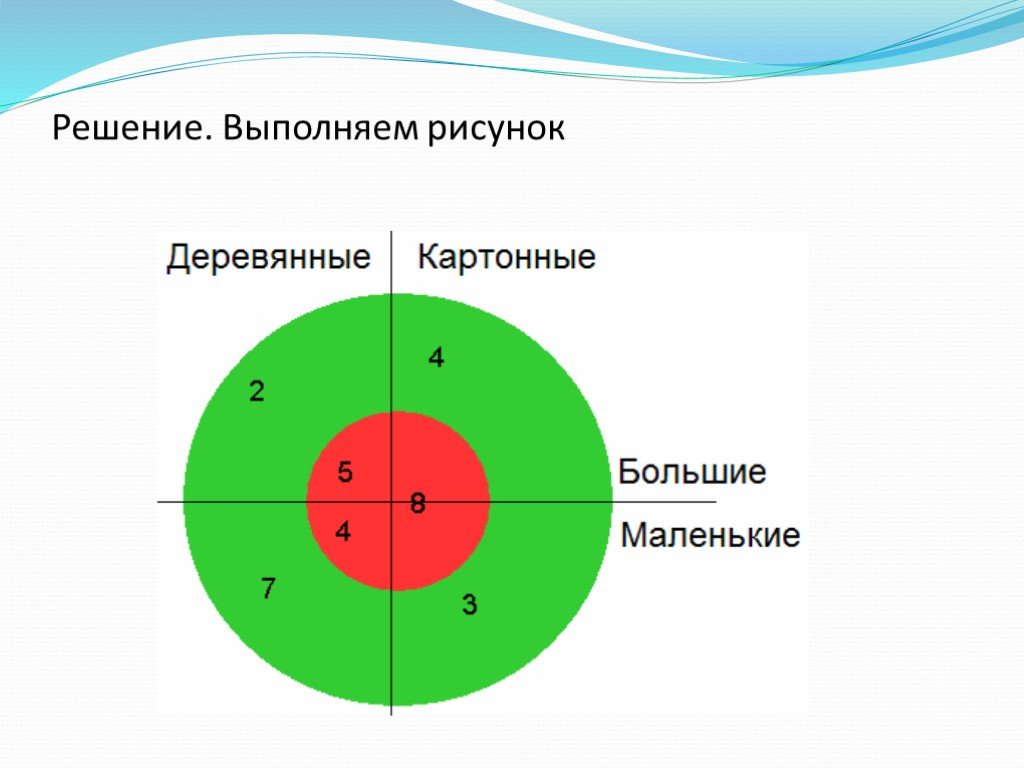
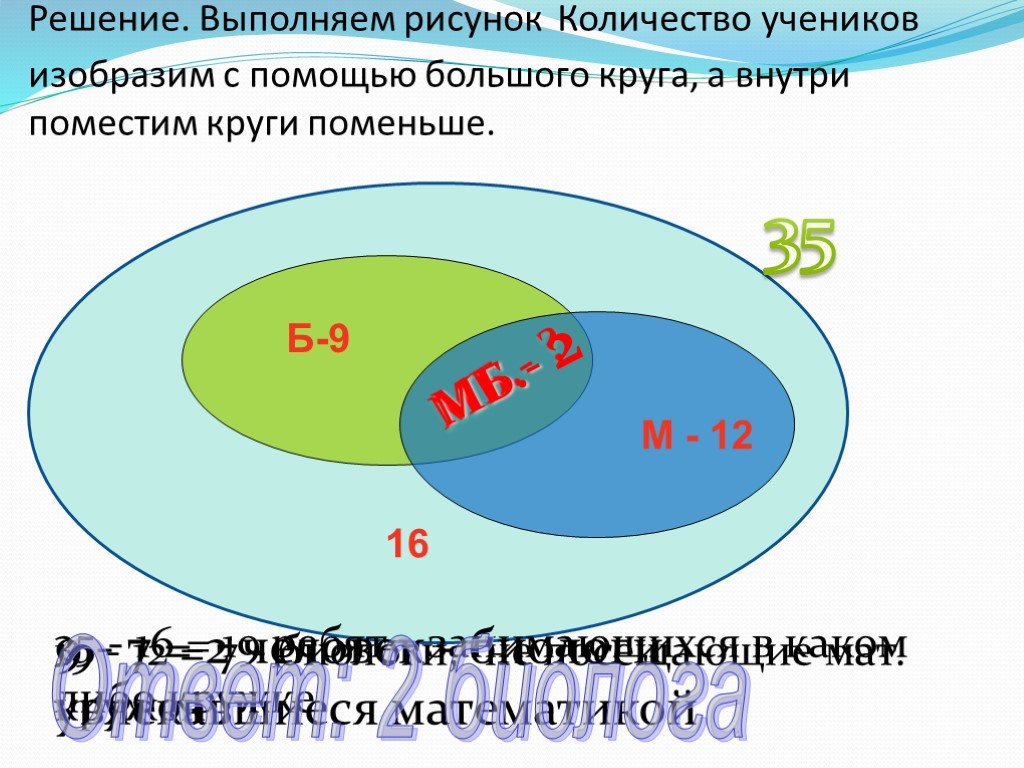
Презентация "Круги Эйлера" (6 класс) по математике – проект, доклад
Презентацию на тему "Круги Эйлера" (6 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 21 слайд(ов).
Слайды презентации
Список похожих презентаций
Круги Эйлера
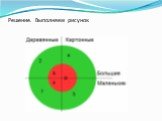
№1. Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги ...Круги Эйлера
Леонард Эйлер. Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал ...Круги Эйлера
Круги Эйлера. Один из величайших математиков петербургский академик, за свою долгую жизнь он написал более 850 научных работ. В одной из них появились ...Деление и обобщение понятий. Круги Эйлера-Венна
Деление понятий. . ! Деление понятия — это мысленное действие: перечисление видовых понятий, которые входят в родовое понятие. . ! Слово, обозначающее ...Решение логических задач с помощью кругов Эйлера
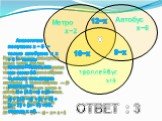
Из 90 туристов, отправляющихся в путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Решение: Покажем условие задачи ...Круг Эйлера
Выполнила:. Жубанова Диана ученица 7 класса Карасаевской СОШ. Цель исследования: Изучить круги Эйлера Научиться применять данный способ для решения ...Знакомство с теоремой Эйлера
Теорема Эйлера- математическое утверждение, связывающее между собой число ребер, граней и вершин многогранников. Она хорошо известна и присутствует ...Замысловатые маршруты Эйлера
Кенигсбергские мосты А, В, С, D – части континента, отделённые друг от друга а, b, с, d, e, f, g – мосты А, В, С, D – узлы(вершины) а, b, с, d, e, ...Теорема Эйлера и ее применение
ТЕОРЕМА ЭЙЛЕРА. Из приведенной таблицы непосредственно видно, что для всех выбранных многогранников имеет место равенство В - Р + Г = 2. Оказывается, ...Задача Эйлера
Теорема Эйлера. Теорема. Для связного простого графа имеет место равенство В - Р + Г = 2, где В - число вершин, Р - общее число ребер, Г - число областей ...Поворот и геометрия
ВСПОМИНАЕМ. Что называют параллельным переносом на заданный вектор? На что при параллельном переносе отображается прямая? Является ли параллельный ...Неевклидова геометрия
Мы выбрали эту тему так как она нас очень заинтересовала тем , что геометрия Лобачевского очень полезна в современном мире, и мы хотим немного рассказать ...Перпендикулярность в пространстве геометрия
Цель:. Познакомиться с перпендикулярностью в пространстве. Проанализировать различные источники по данной теме. Выделить основные подходы к рассмотрению ...Что такое геометрия
Геометрия- одна из наиболее древних наук. Первые геометрические факты были найдены…. В Вавилонских клинописных таблицах и египетских папируса (III ...«Ломаная» геометрия
Найдите соответствие. Ответы. Ломаная Тема урока:. Какие из фигур являются ломаными? А Б В Г Д. Ответ А В Г. Кусок проволоки возьми И его ты перегни. ...Пчелы и геометрия
Внеклассное мероприятие «пчелы и геометрия». В природе все продумано и совершенно. Индийская пчела Украинская пчела. Австралийская пчела. Пчела - ...Фракталы – геометрия природы
Задачи:. узнать, что такое «фракталы»; изучить историю возникновения и развития фрактальной геометрии; ознакомиться с биографией создателя фракталов ...Математика геометрия
ГЛАВА 1. История математики. ГЛАВА 2. Математика. ГЛАВА 3. Геометрия И последнее…. Что такое математика. Она изучает числа и величины, отношения и ...Наглядная геометрия
геометрия Урок 1. Сегодня мы отправляемся в путешествие в удивительную страну, которая называется ГЕОМЕТРИЯ. Что такое геометрия? Какими инструментами ...Алгебра и геометрия
Комплексные числа. ׳. Содержание. § 1. Основные понятия § 2. Геометрическое изображение комплексных чисел § 3. Формы записи комплексных чисел § 4. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2018
Категория:Математика
Классы:
Содержит:21 слайд(ов)
Поделись с друзьями:
Скачать презентацию