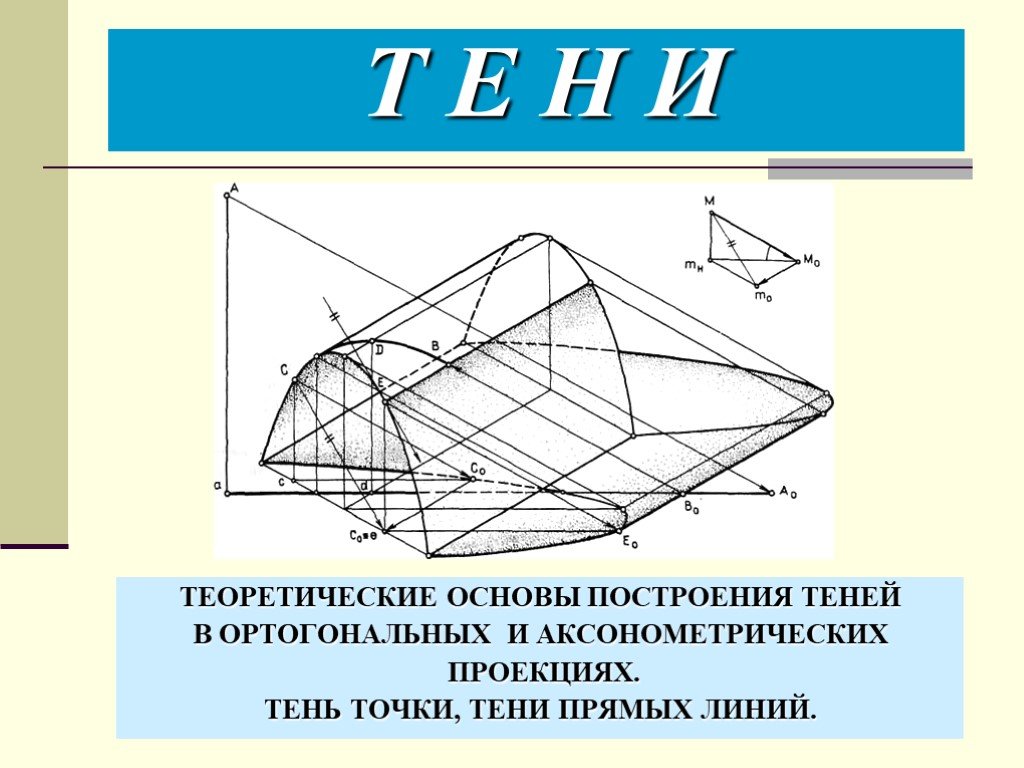
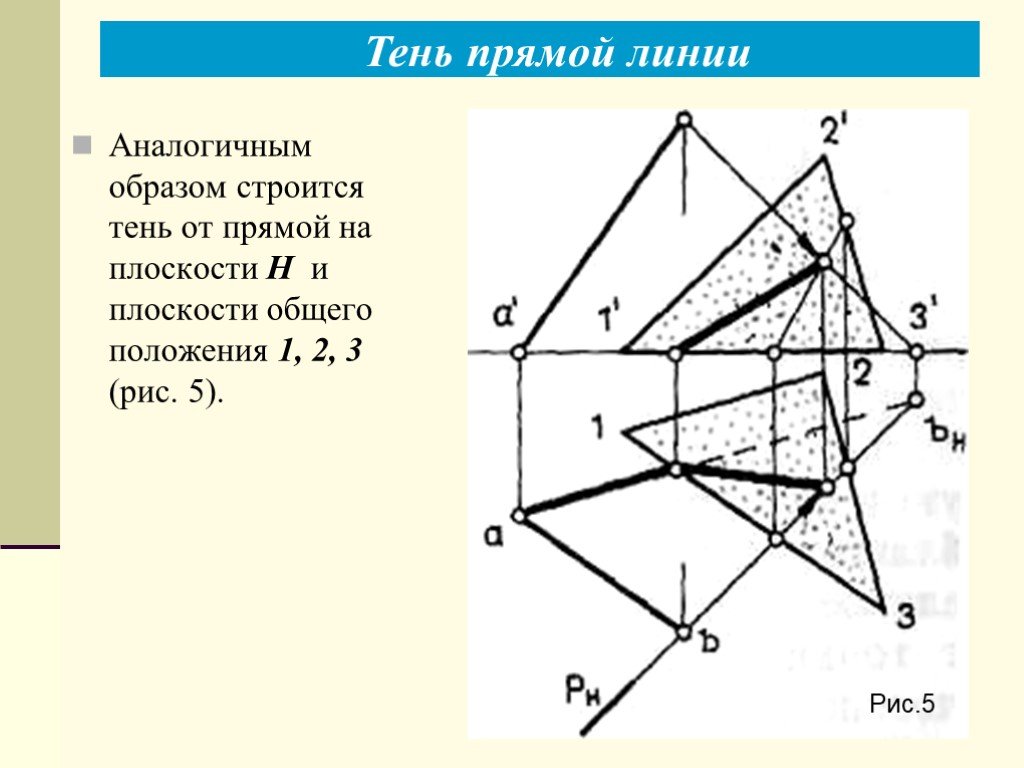
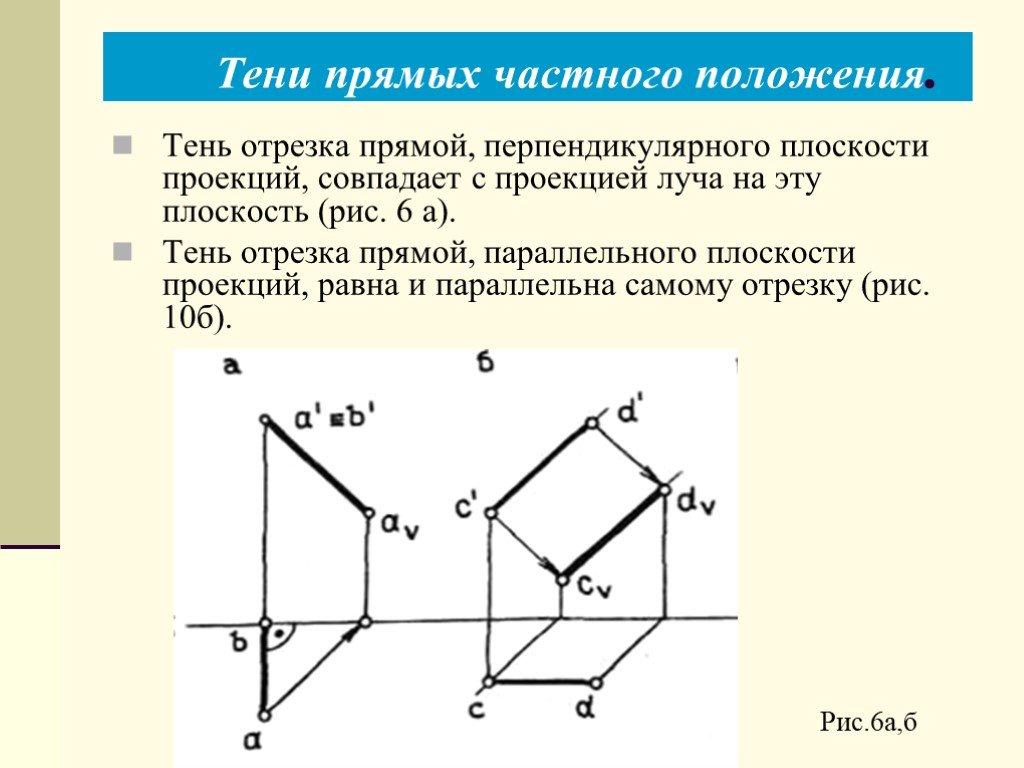
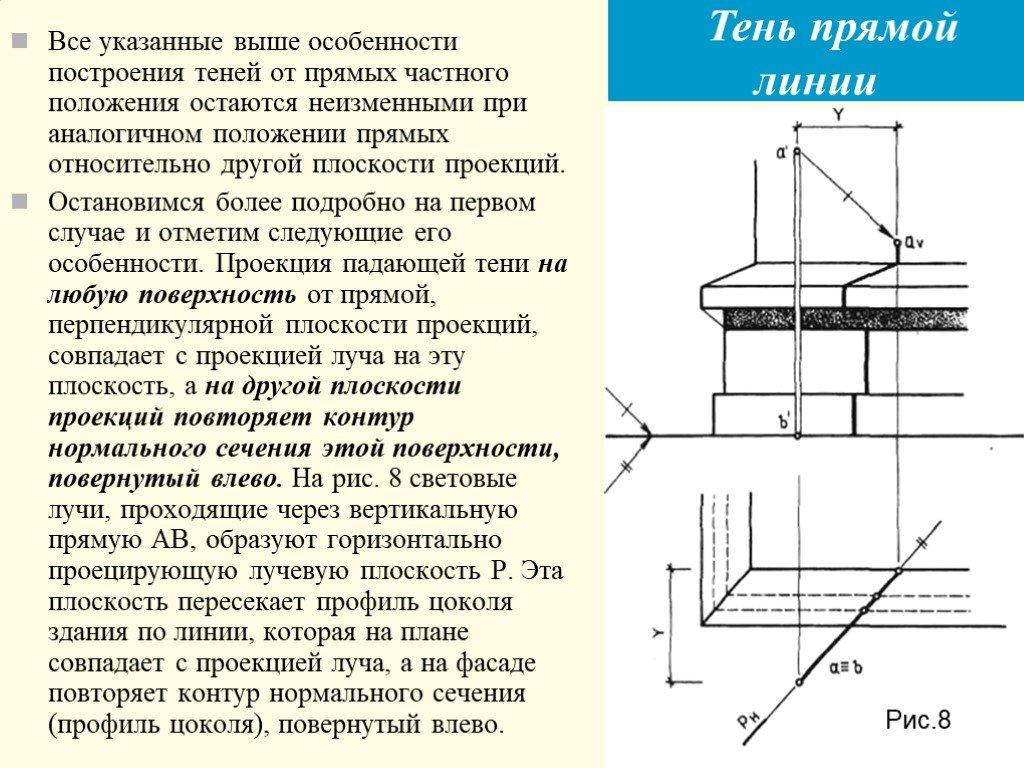
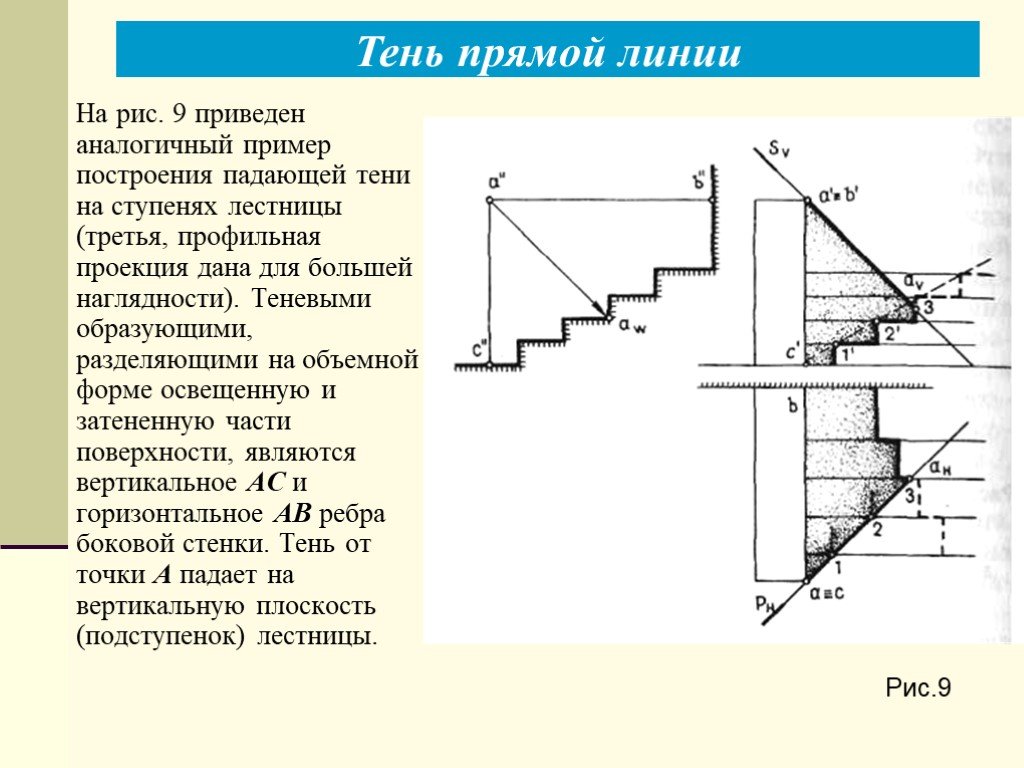
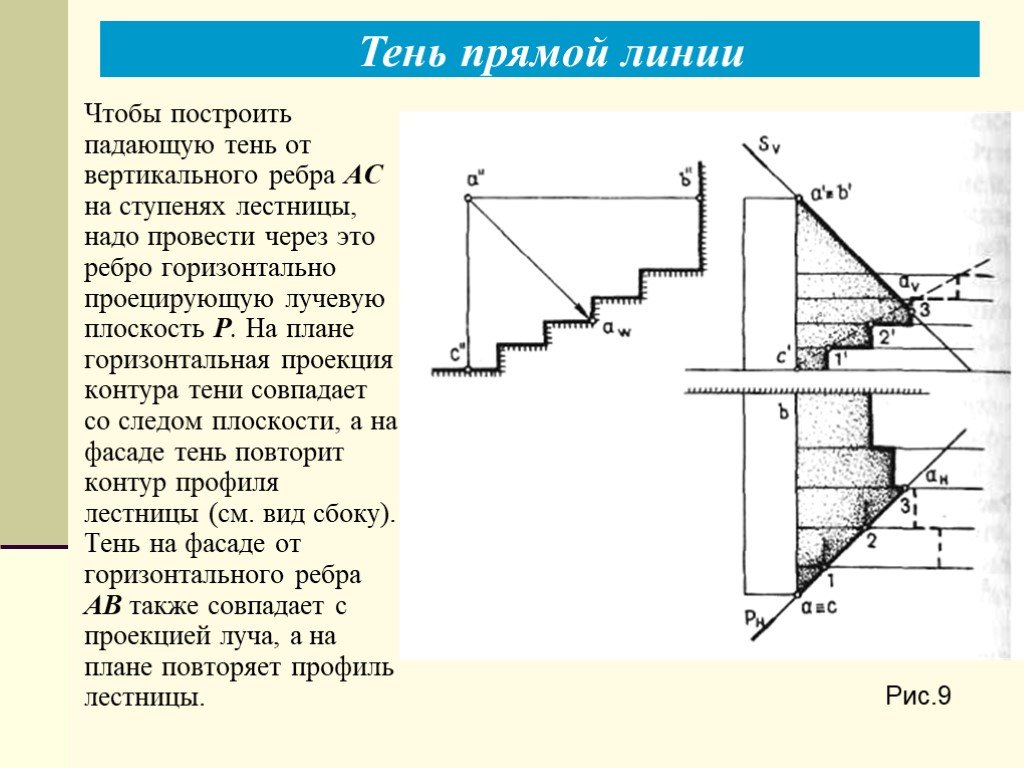
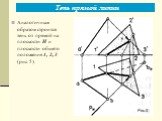
Презентация "Теоретические основы построения теней в ортогональных и аксонометрических проекциях. Тень точки, тени прямых линий" по математике – проект, доклад
Презентацию на тему "Теоретические основы построения теней в ортогональных и аксонометрических проекциях. Тень точки, тени прямых линий" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
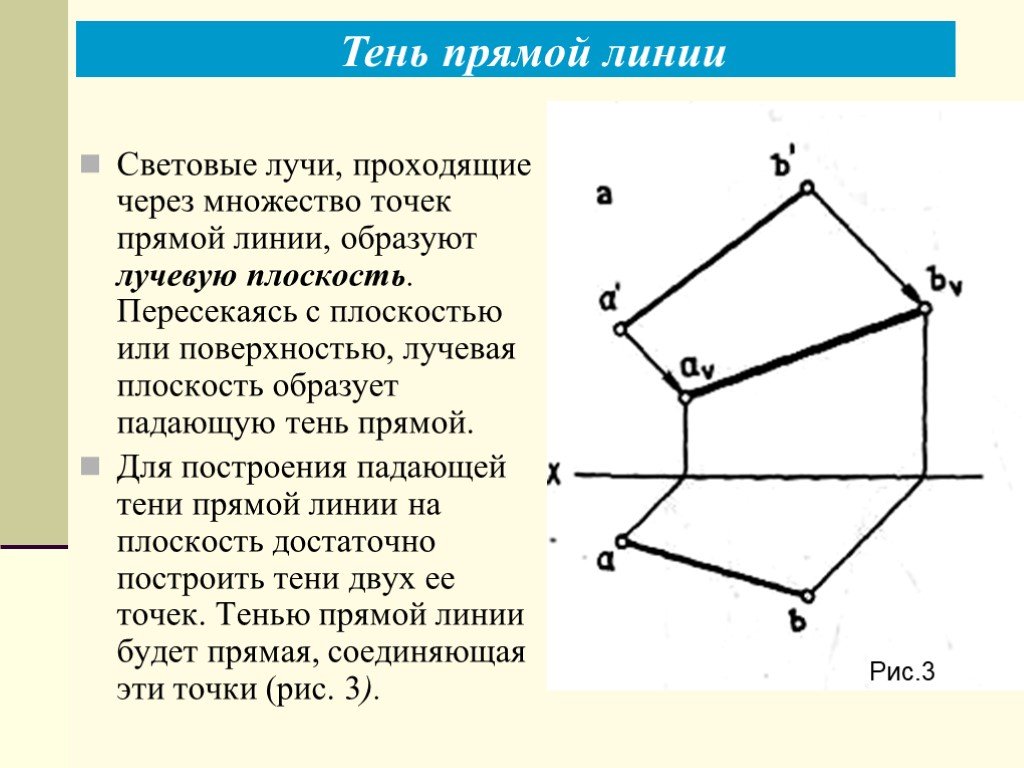
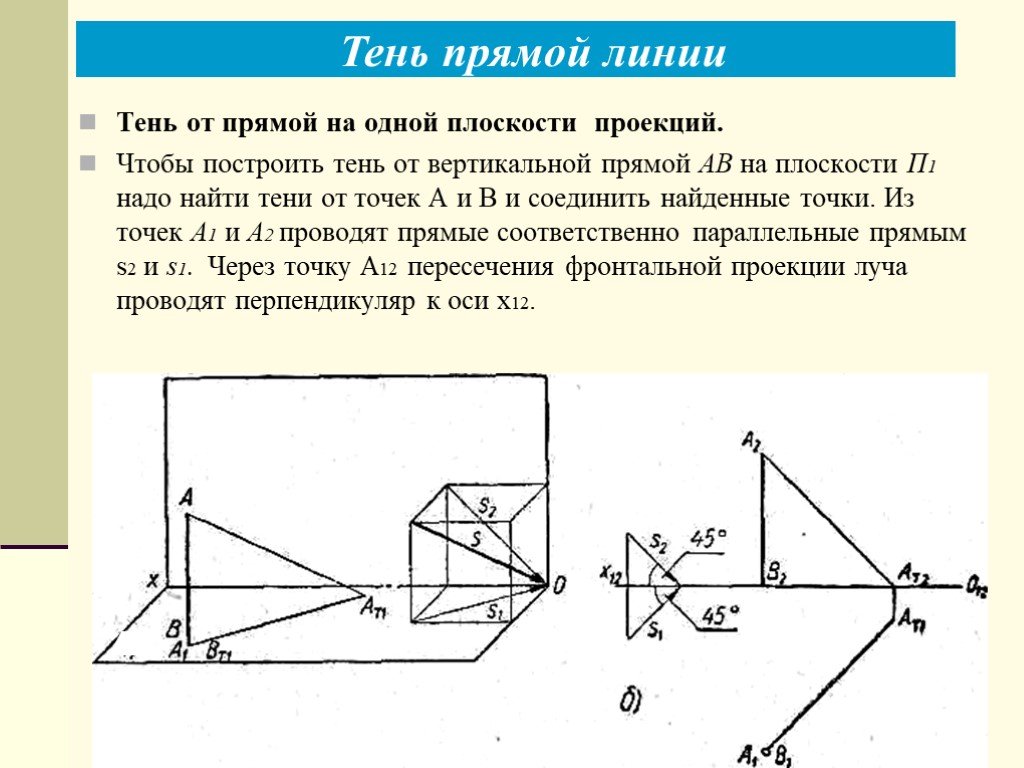
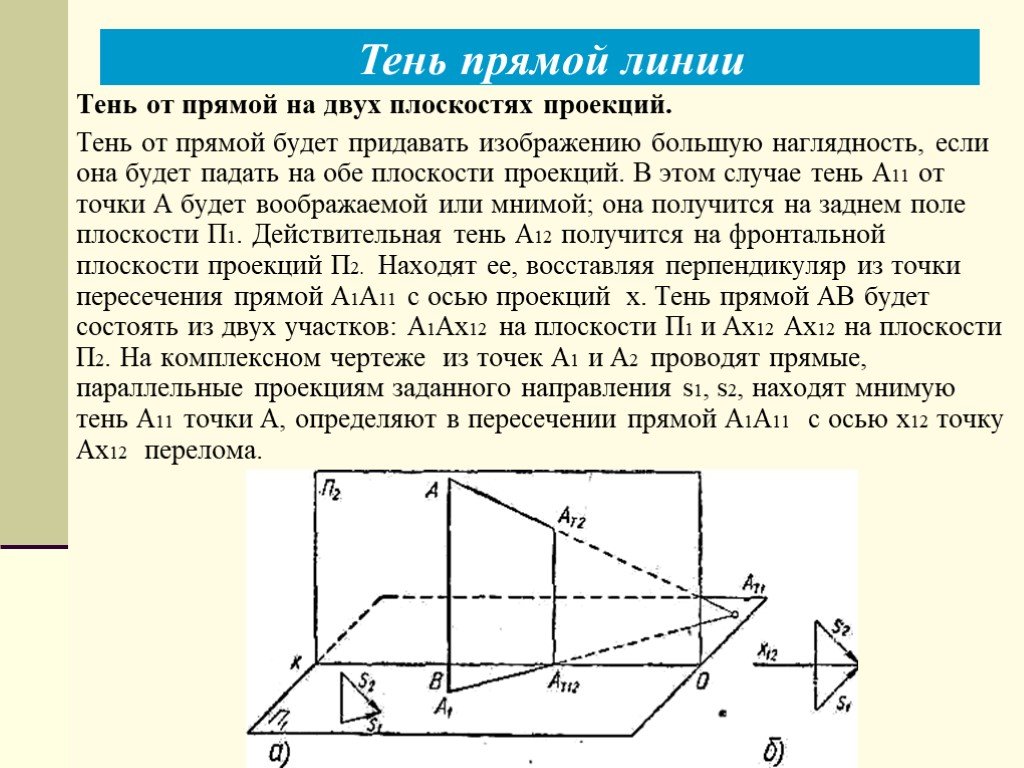
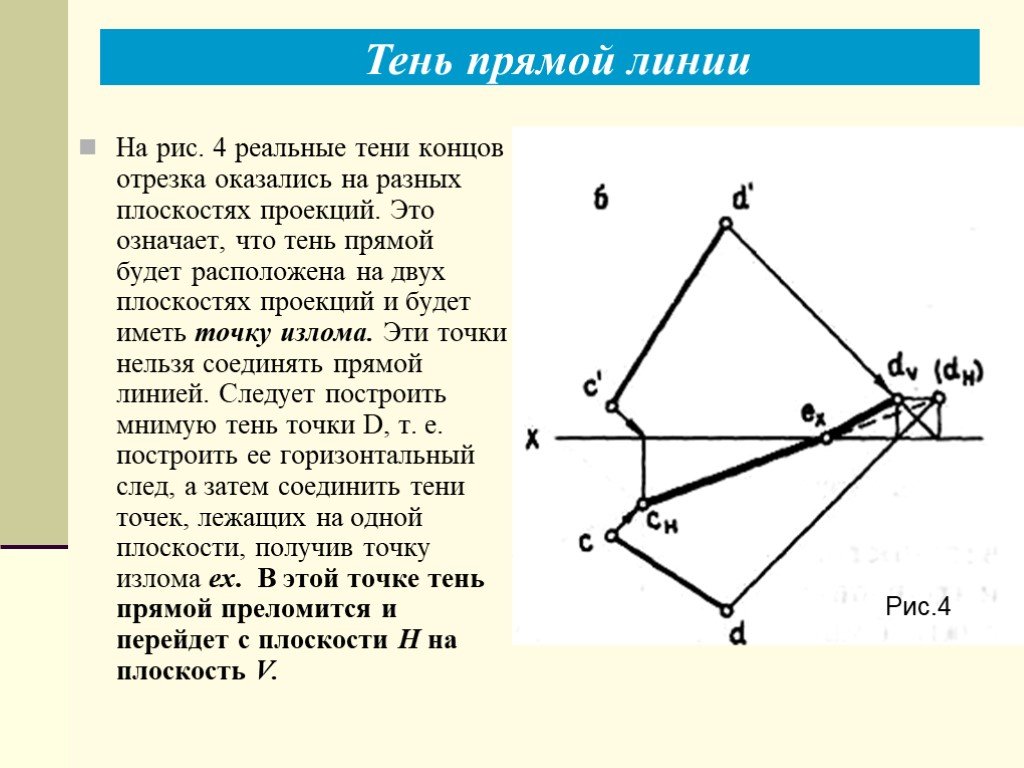
Слайды презентации
Список похожих презентаций
"Взаимное расположение прямых в пространстве. Угол между двумя прямыми
«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия». Дьердье Пойа, венгерский математик. ..."Симметрия в архитектуре Старого Оскола"
Остановка 1. Главная улица города – улица Ленина. Мы находимся в центре нашего города у здания администрации. Какие приемы использовал архитектор, ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ..."Комбинаторика и вероятность"
Диктант ******- это раздел математики, посвященный задачам выбора и расположения предметов из различных множеств. Произведение натуральных чисел от ..."Сложение и вычитание рациональных чисел"
I. II. III. IV. Тема: "Сложение и вычитание положительных и отрицательных чисел". Станции: Историческая Биологическая Географическая Математическая. ...«Правильные и неправильные дроби»
«Учёные Грузии нашли золото в составе крови человека». Из журнальной статьи. “ЗОЛОТАЯ КРОВЬ” (ЭДУАРД АСАДОВ). Не так давно учёные открыли Пусть небольшой, ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ..."Турнир веселых и смекалистых знатоков истории, физики, химии, математики"
Цели мероприятия: 1.Развитие у учащихся интереса к изучаемым предметам. 2.Показать необходимость знаний по математике в других науках. 3.Формирование ...«Симметрия в пространстве» геометрия
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной ...Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии. 1)Какова бы ни была плоскость, существуют точки, принадлежащие ей и точки, не принадлежащие ей. 2) Если две плоскости имеют ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ..."Смешанные дроби. Представление смешанного числа в виде неправильной дроби".
Смешанные дроби. Представление смешанного числа в виде неправильной дроби. 02.03. Определите координаты точек А, В, С и М. ...Аксиома параллельных прямых
Аксиомами называются те основные положения геометрии, которые принимаются в качестве исходных положений, на основе которых доказываются далее теоремы ...«Действия с дробями», «Нахождение дроби и процентов от числа»
Систематизация знаний по темам: «Действия с дробями», «Нахождение дроби и процентов от числа», Отработка практических навыков выполнения действий ..."Функция y = kx², ее свойства и график". 8-й класс
Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ...«Сложение и вычитание десятичных дробей»
Чтобы сложить (вычесть) десятичные дроби, нужно: 1) уравнять в этих дробях количество знаков после запятой; 2) записать их друг под другом так, чтобы ...«Параллельность прямых и плоскостей»
ABCD – трапеция, AD , E и F – середины AB и CD соответственно. Докажите, что EF ǁ α. α. α. α. α. A B C D α. Через вершины А и С параллелограмма ABCD ...«Математика в профессиях»
Ознакомление с типами профессий и характеристиками труда. Исследование значения математики в различных областях деятельности человека. Развитие познавательной ...Аксиома параллельных прямых
Теорема Теорема Теорема Теорема. Об аксиомах геометрии. А на чём основаны доказательства самых первых теорем геометрии? На аксиомах. Утверждениях ...«Треугольники и их виды»
Геометрические фигуры. а ж е д с б и з. Треугольники и их виды. Определение треугольника, элементы треугольника Виды треугольников Сумма углов треугольника ...Конспекты
Аксиома параллельных прямых
Кондручина Надежда Сергеевна,. . учитель математики МКОУ «Панкрушихинская сош»,. . Панкрушихинский район Алтайского края. Предмет:. Геометрия. ...Аксиома параллельных прямых
Открытый урок геометрии в 7 классе. Тема урока: «Аксиома параллельных прямых». Дата проведения урока: 16 января 2014 года. Учитель: Олейникова ...I признак равенства треугольников в задачах
ТЕМА УРОКА:. I. признак равенства треугольников в задачах. ТИП УРОКА. : закрепление изученного материала. КОНТИНГЕНТ УЧАЩИХСЯ:. 7 класс. ...Арифметический квадратный корень и его свойства
Конспект урока математики в 10 классе. Жирнова С.В. учитель математики. Тема урока:. «Арифметический квадратный корень и его свойства». Тип урока. ...Веселая и полезная математика
. Тюрина Валентина Викторовна. 1 квалификационная категория – учитель математики. Город Прокопьевск Кемеровская область. МКОУ «Школа – интернат ...Алгоритм и его свойства. Запись алгоритмов. Виды алгоритмов
Алгоритм и его свойства. Запись алгоритмов. Виды алгоритмов. . КАЗАХСТАН. ЮЖНО-КАЗАХСТАНСКАЯ ОБЛАСТЬ. Г.ШЫМКЕНТ, ОСНОВНАЯ СРЕДНЯЯ ШКОЛА №97. ...Арифметический квадратный корень и его свойства
Тема: «Арифметический квадратный корень и его свойства». Урок-игра «Аукцион математических знаний». Цели урока. :. . Образовательные:. - ...Вероятность и математическая статистика
Открытый урок. . по учебной дисциплине Теория вероятностей и математическая статистика. Тема: «Вероятность и математическая статистика». Группа ...Арифметический корень натуральной степени и его свойства
Урок алгебры в 9 классе. . Тема урока. : «Арифметический корень натуральной степени и его свойства». . Из опыта работы учителя математики. ...Арифметический квадратный корень из произведения, степени и дроби
Тема: «Арифметический квадратный корень из произведения, степени и дроби». Цели урока:. . Образовательные:. изучить основные свойства квадратных ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:20 мая 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию