Презентация "Тригонометрические формулы" (10 класс) по математике – проект, доклад
Презентацию на тему "Тригонометрические формулы" (10 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
Тригонометрические формулы
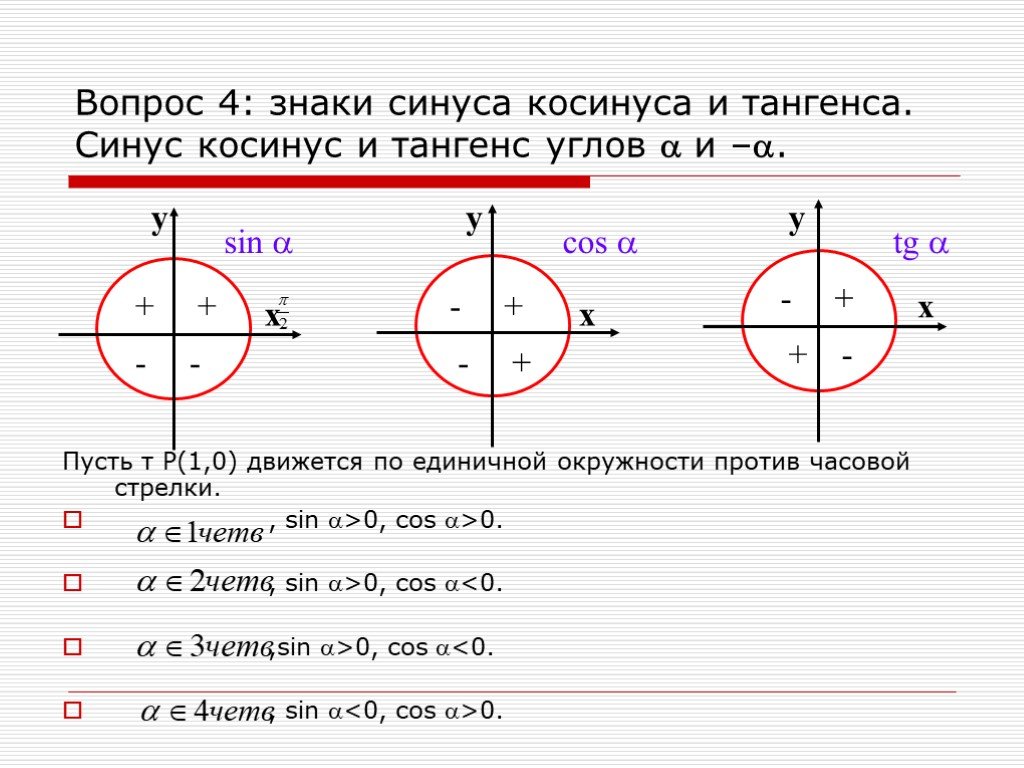
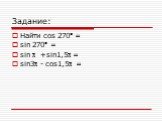
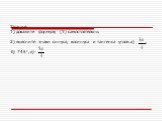
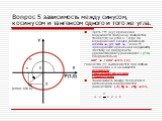
Математический турнир. Тур I. В какой четверти лежит угол α, если выполняется условие Sinα>0, cosα. Определите знак значения функции cos150˚ ( « - ...Тригонометрические формулы
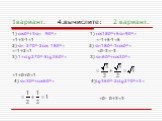
Цель урока. Повторить и систематизировать изученный материал Подготовиться к контрольной работе. Задачи урока. Повторить определение синуса, косинуса, ...Основные тригонометрические формулы
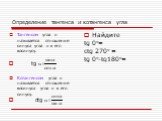
Основные формулы тригонометрии и их свойства. Дадим определения тригонометрическим функциям синуса, косинуса, тангенса и котангенса. возьмем любой ...Тригонометрические функции одного и того же аргумента
Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной ...Тригонометрические функции
Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника 1) Синус - отношение противолежащего катета ...Тригонометрические функции
Содержание. Введение................................................... .......3-5слайд Начало изучения..............................................6-7 ...Тригонометрические уравнения. Арксинус
cos t = a cos t = 2/5 С О А В D х у М(t1) P(t2) x=2/5 Рис. 1 t = t1 + 2πκ, t = t2 + 2πκ,. где t1 – длина дуги АМ, а t2 = - t1. t1 є [ 0; π/2 ] arccos ...Тригонометрические уравнения и их решения
Решение квадратного уравнения. ax²+bx+c =0 D= b²-4ac X = -b±√D __. arcsin a Є [-π/2; π/2] arccos a Є [0; π] arctg a Є (-π/2; π/2). Обратные тригонометрические ...Интерполяционные формулы
Пусть точка х лежит в окрестности середины интервала содержащего 2n+1 равноотстоящих с шагом h узла интерполирования. Для интерполирования функции ...Ремонт дома. Расход материала. Вычисления и формулы
Цель:. Определить квадратуру дома. Определить квадратуру всех комнат. Выяснить, сколько определенного материала потребуется для ремонта дома. Задачи:. ...Приближенные формулы в схеме Бернулли
Локальная формула Муавра-Лапласа. Если , то где. Свойства функции Четная . При. Формула Пуассона Если и , то где. Интегральная формула Муавра-Лапласа. ...Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа.
1. У = - f(x) ← y = f(x) , симметрия относительно оси ОХ. 2. У = f(- x) ← y = f(x), симметрия относительно оси ОУ. 3. У = - f (- x) ← y = f(x), симметрия ...Основные формулы тригонометрии
Содержание. Из истории… 2) Основные тригонометрические формулы а) основные тригонометрические тождества б) формулы сложения в) формулы суммы и разности ...Основные формулы тригонометрии
Могут ли одновременно выполняться равенства? Правильный ответ: Да 17.06.2019. . Нет. Вычислите:. учитель математики Кустова М.О. . - 0,6. . . . . ...Определение запыленности воздуха по листьям деревьев с использованием формулы Пика
Введение. В последние годы, наряду с изменениями климата, происходит значительное увеличение антропогенной нагрузки на природные и урбанизированные ...Тригонометрические функции углов в произвольном треугольнике 1-2
Продолжите фразу:. Синусом острого угла прямоугольного треугольника называется. А С В. отношение противолежащего катета к гипотенузе. Косинусом острого ...Тригонометрические функции углового аргумента - алгебра,
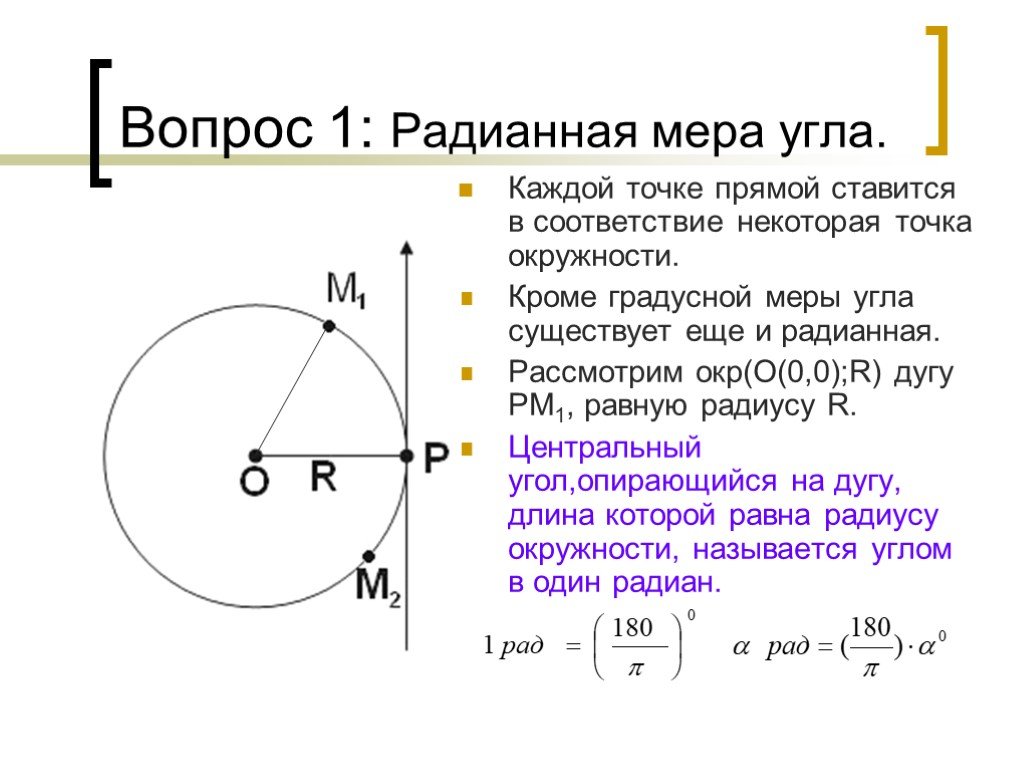
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Решение задач с использованием формулы полной вероятности и формулы Бейеса
Формула полной вероятности. Формула Бейеса P(Hi|A) = =. Задачи. 1. В сборочный цех поступили детали с трех станков. На первом станке изготовлено 51% ...Тригонометрические уравнения
Тригонометрические уравнения. Уравнение представляет собой наиболее серьёзную и важную вещь в математике. О.Лодж. «Дороги не те знания, которые откладываются ...Решение комбинаторных задач с помощью бинома Ньютона и полиномиальной формулы
Цель: Задачи:. изучить и применить бином Ньютона и полиномиальную формулу к решению некоторых комбинаторных задач. 1) ознакомиться с формулой бинома ...Конспекты
Тригонометрические формулы
Ельцова Н.Г., учитель МОУ «Гимназия № 11». Урок по теме: «Тригонометрические формулы ». . . Класс:. 10 гуманитарный. Цель:. 1.Ввести понятие ...Тригонометрические формулы
Тема: Тригонометрические формулы (25 часов). Урок 6 – 7: Зависимость между синусом, косинусом и тангенсом одного и того же угла. Цель:. изучить ...Тригонометрические формулы
Алгебра 10 класс. Разработал:учитель математики первой категории. МАОУ УЛу-Юльской СОШ. Олей В.И. Тема урока:Тригонометрические формулы. Вид ...Тригонометрические уравнения. Соs х = а
ТЕМА УРОКА. :. . учителя математики. . МБОУ СОШ № 24. . города Тамбова. Максимович Надежды Васильевны. Цели урока. ...Тригонометрические уравнения, сводящиеся к простейшим
Методическая разработка урока. . . МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА по теме. «Тригонометрические уравнения, сводящиеся к простейшим». УЧИТЕЛЬ:. ...Тригонометрические выражения и их преобразования
. Воронкова Ольга Ивановна. МБОУ «Средняя общеобразовательная школа. . № 18». г. Энгельса Саратовской области. . . Учитель математики. ...У математики существует свой язык – это формулы
. « У математики существует свой язык – это формулы. ». С. Ковалевская. ФОРМУЛЫ . СОКРАЩЕННОГО УМНОЖЕНИЯ. 7 класс. Цели:. 1. Обобщить ...Тригонометрические функции острого угла
МКОУ СОШ с.п.Кара-Суу Черекского района КБР. Айшаева Фердаус Сулеймановна. . "Тригонометрические функции острого угла" Геометрия 8 класс. ...Тригонометрические уравнения
Конспект урока алгебры и начала анализа в 11 классе. по теме: «Тригонометрические уравнения (урок обобщения и систематизации знаний)». учителя ...Тригонометрические уравнения
Тема урока «Тригонометрические уравнения» (2 часа). Тригонометрия по традиции занимает большое место в материалах конкурсных экзаменов в вузы; ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:17 ноября 2018
Категория:Математика
Классы:
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию