Презентация "Тригонометрические уравнения. Арксинус" по математике – проект, доклад
Презентацию на тему "Тригонометрические уравнения. Арксинус" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
Слайды презентации
Список похожих презентаций
Тригонометрические уравнения и их решения
Решение квадратного уравнения. ax²+bx+c =0 D= b²-4ac X = -b±√D __. arcsin a Є [-π/2; π/2] arccos a Є [0; π] arctg a Є (-π/2; π/2). Обратные тригонометрические ...Тригонометрические уравнения. Методы решений
История тригонометрии. Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников (trigwnon - треугольник, а metrew- ...Арксинус. Решение уравнения sin t = a
Цели. Изучить определение арксинуса числа. Изучить формулы решения простейшего тригонометрического уравнения sin t = a. Повторим. Что называется синусом ...Тригонометрические уравнения и методы их решения
«Великая книга природы открыта для нас, но научиться понимать ее можно лишь путем прилежания, любви, страданий. Язык этот-математика. Математика расцветает ...Тригонометрические уравнения
Верно ли, что:. Имеют ли смысл выражения:. Решить уравнение:. Пример 1. Решить уравнение 2 sin2x + sinx - 1 = 0. Решение. Введём новую переменную ...Тригонометрические уравнения
Тригонометрические уравнения. Уравнение представляет собой наиболее серьёзную и важную вещь в математике. О.Лодж. «Дороги не те знания, которые откладываются ...Тригонометрические уравнения
Цели урока:. Повторить основные формулы и методы решения тригонометрических уравнений; Закрепить умения и навыки решения тригонометрических уравнений;. ...Тригонометрические уравнения
I. Повторение и актуализация. 1. Что значит простейшая тригонометрическая функция? 2. Приведите пример простейшего тригонометрического уравнения. ...Тригонометрические уравнения
Определения тригонометрических функций. Синусом угла х называется. ордината точки единичной окружности, полученной из точки (1; 0) поворотом на угол ...Простейшие тригонометрические уравнения
I. Вычисли устно:. II. Найди ошибку при решении неравенства:. III. Для каждого рисунка подберите соответствующее уравнение. А) Б) В) Г). sin t=a cos ...Тригонометрические уравнения
SINx=a (ǀaǀ≤1) Пример: Sinx=1/2 Решение Частные случаи. COSx=a (ǀaǀ≤1). tgx=a Пример: tgx=1. ctgx=a. Пример: ctgx=1. Пример: COSx=1/2. ...Простейшие тригонометрические уравнения
Определение тригонометрии. Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника. История тригонометрии. ...Простейшие тригонометрические уравнения
История развития тригонометрии. . . . . . . . . . . Устная работа. Ответьте на вопросы:. Может ли косинус быть равным: 0,75; 5/3; -0,35; π/3; 3/π; ...Однородные тригонометрические уравнения
Кроссорд. 1. Значение переменной, обращающее уравнение в верное равенство 2. Единица измерения углов 3. Числовой множитель в произведении 4. Раздел ...Показательные уравнения
Показательные. Цели урока: 1. ввести понятие показательных уравнений; 2. формировать умение решать показательные уравнения основными методами: функционально-графическим, ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0. 1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...Формула корней квадратного уравнения
Вы хотите научиться решать квадратные уравнения? ДА НЕТ. . . Содержание. Определение квадратного уравнения Дискриминант квадратного уравнения Формула ...Тригонометрические функции углового аргумента
Цель урока: отработка навыка нахождения значений тригонометрических функций углового аргумента. Задачи: 1.обобщить и систематизировать учебный материал ...Тригонометрические формулы
Математический турнир. Тур I. В какой четверти лежит угол α, если выполняется условие Sinα>0, cosα. Определите знак значения функции cos150˚ ( « - ...Дифференциальные уравнения высших порядков
1. Общие сведения. Определение. Дифференциальное уравнение содержащее производную функции двух и более порядков, называется дифференциальным уравнением ...Конспекты
Тригонометрические уравнения, сводящиеся к простейшим
Методическая разработка урока. . . МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА по теме. «Тригонометрические уравнения, сводящиеся к простейшим». УЧИТЕЛЬ:. ...Однородные тригонометрические уравнения
«Однородные тригонометрические уравнения». (алгебра и начала анализа, 10 класс). Пронина Светлана Михайловна. учитель математики. ГБОУ СОШ ...Тригонометрические уравнения. Соs х = а
ТЕМА УРОКА. :. . учителя математики. . МБОУ СОШ № 24. . города Тамбова. Максимович Надежды Васильевны. Цели урока. ...Тригонометрические уравнения
Урок соревнование. Тема. «Тригонометрические уравнения». Девиз урока. :. «. Один за всех и все за одного». Ход урока:. Урок –соревнование будет ...Тригонометрические уравнения
. Конспект урока по алгебре в 10 классе. Автор: Березовская Дарья Ивановна. учитель математики МБОУ «Сухинская СОШ». Тема: Тригонометрические ...Тригонометрические уравнения
Конспект урока алгебры и начала анализа в 11 классе. по теме: «Тригонометрические уравнения (урок обобщения и систематизации знаний)». учителя ...Тригонометрические уравнения
Захарова Людмила ВладимировнаМБОУ «Средняя общеобразовательная школа № 59» г. Барнаулаучитель математики. zlv-13@mail.ru. ...Тригонометрические уравнения
Урок-игра по алгебре и началам анализа в10 классе. . Тема «Тригонометрические уравнения». Девиз урока: . “Один за всех и все за одного”. Цель:. ...Простейшие тригонометрические уравнения
Разработка урока в 10 классе. Тема урока:. Простейшие тригонометрические уравнения. Цель урока:. Образовательные:. . . - актуализировать ...Тригонометрические уравнения
Тема урока «Тригонометрические уравнения» (2 часа). Тригонометрия по традиции занимает большое место в материалах конкурсных экзаменов в вузы; ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 августа 2019
Категория:Математика
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию



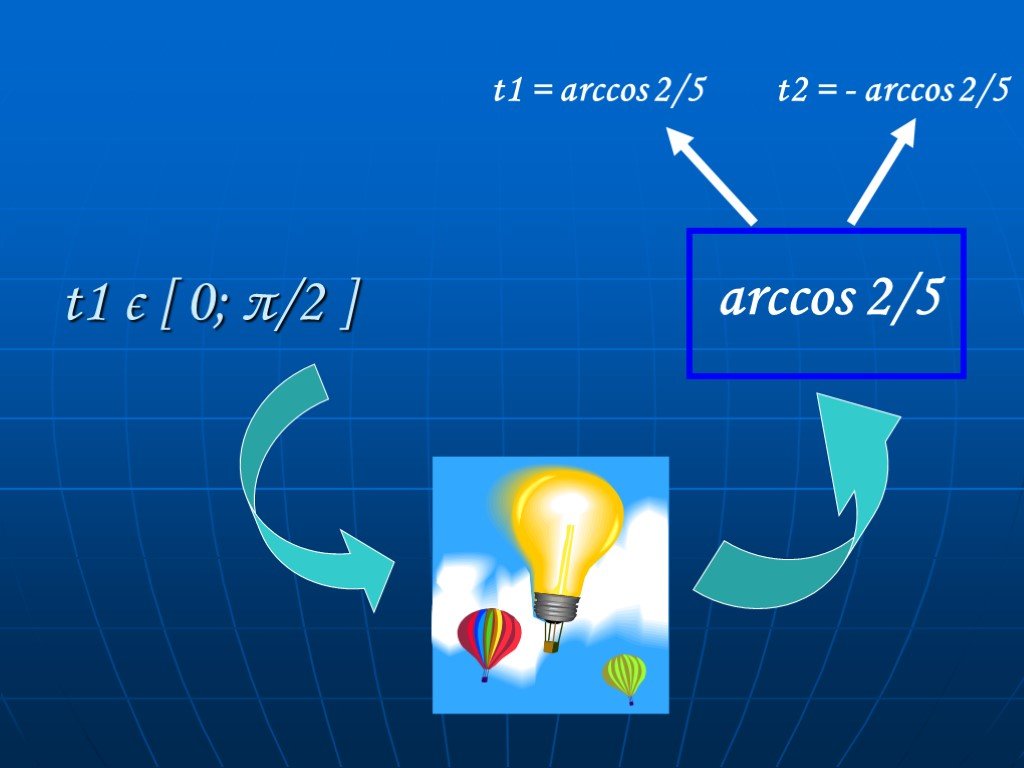
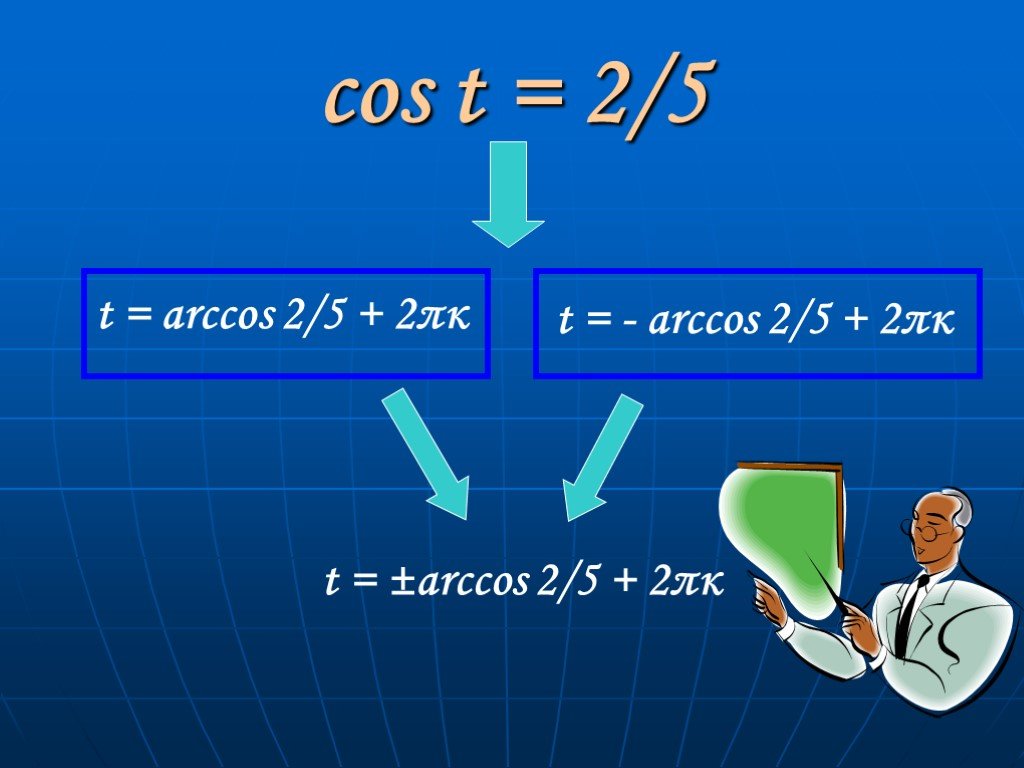


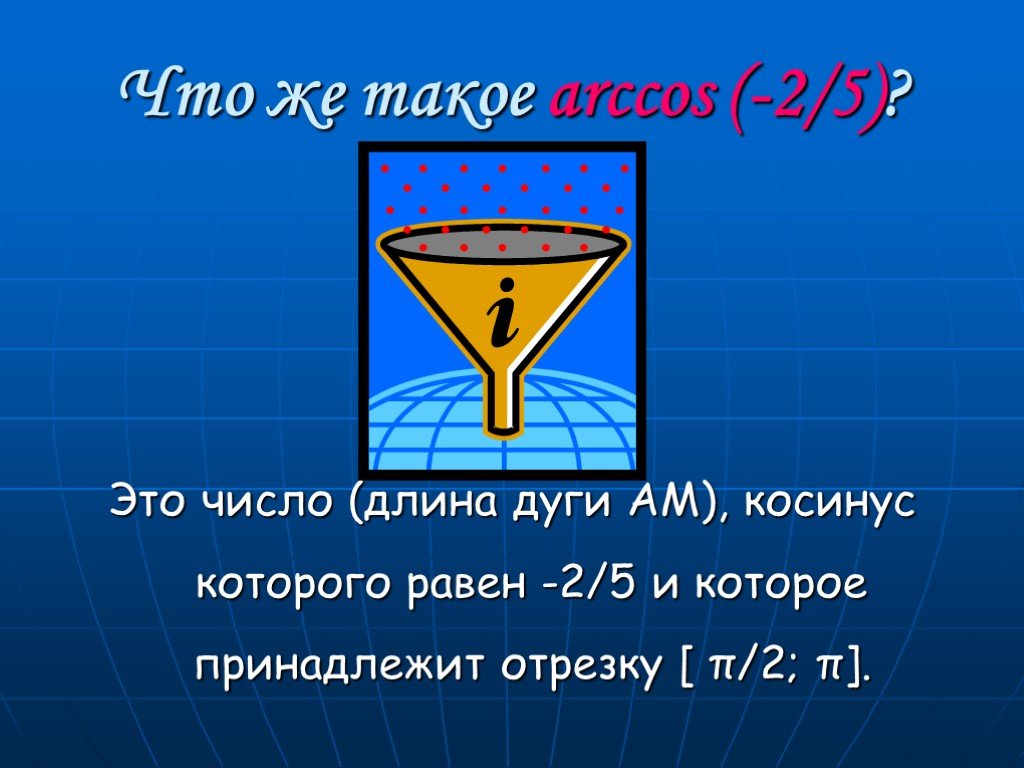







![t1 є [ 0; π/2 ] arccos 2/5 t1 = arccos 2/5 t2 = - arccos 2/5 t1 є [ 0; π/2 ] arccos 2/5 t1 = arccos 2/5 t2 = - arccos 2/5](https://prezentacii.org/upload/cloud/19/08/157191/images/thumbs/screen3.jpg)
![Что же такое arccos 2/5? Это число (длина дуги АМ), косинус которого равен 2/5 и которое принадлежит отрезку [ 0; π/2 ]. Что же такое arccos 2/5? Это число (длина дуги АМ), косинус которого равен 2/5 и которое принадлежит отрезку [ 0; π/2 ].](https://prezentacii.org/upload/cloud/19/08/157191/images/thumbs/screen5.jpg)

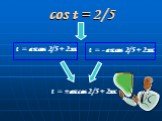
![Что же такое arccos (-2/5)? Это число (длина дуги АМ), косинус которого равен -2/5 и которое принадлежит отрезку [ π/2; π]. Что же такое arccos (-2/5)? Это число (длина дуги АМ), косинус которого равен -2/5 и которое принадлежит отрезку [ π/2; π].](https://prezentacii.org/upload/cloud/19/08/157191/images/thumbs/screen7.jpg)
![Определение. Если |а|≤1, то arccos a (арккосинус а) – это такое число из отрезка [ 0; π], косинус которого равен а. Если |а|≤1, то arccos a = t. cos t =a, 0 ≤ t ≤ π. Определение. Если |а|≤1, то arccos a (арккосинус а) – это такое число из отрезка [ 0; π], косинус которого равен а. Если |а|≤1, то arccos a = t. cos t =a, 0 ≤ t ≤ π.](https://prezentacii.org/upload/cloud/19/08/157191/images/thumbs/screen8.jpg)

![Пример. Вычислить: arccos ½ Решение: Пусть arccos ½ = t. Тогда cos t = ½ и t є [ 0; π]. Значит, t = π/3, поскольку cos π/3 = ½ и π/3 є [ 0; π]. Итак, arccos ½ = π/3. Пример. Вычислить: arccos ½ Решение: Пусть arccos ½ = t. Тогда cos t = ½ и t є [ 0; π]. Значит, t = π/3, поскольку cos π/3 = ½ и π/3 є [ 0; π]. Итак, arccos ½ = π/3.](https://prezentacii.org/upload/cloud/19/08/157191/images/thumbs/screen10.jpg)
![Теорема. Для любого а є [-1;1] выполняется равенство arccos a + arccos (-a) = π. - а а М Р. arccos a + arccos (-a) = AM + AP = PC +AP = AC = π Теорема. Для любого а є [-1;1] выполняется равенство arccos a + arccos (-a) = π. - а а М Р. arccos a + arccos (-a) = AM + AP = PC +AP = AC = π](https://prezentacii.org/upload/cloud/19/08/157191/images/thumbs/screen11.jpg)































