Презентация "Дифференциальные уравнения высших порядков" по математике – проект, доклад
Презентацию на тему "Дифференциальные уравнения высших порядков" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 45 слайд(ов).
Слайды презентации
Список похожих презентаций
линейные дифференциальные уравнения первого порядка
Опрос. 1. Какое уравнение называется дифференциальным? Уравнение, содержащее производные искомой функции или её дифференциалы. 3.Что значит решить ...Многочлены и уравнения высших степеней
Пояснительная записка. За минувший век в математике произошли грандиозные изменения, она (впрочем, как и все другие науки) шагнула необыкновенно далеко ...Дифференциальные уравнения первого порядка
Презентация На тему:. «Дифференциальные уравнения. первого порядка». Подготовил студент группы К-11 Свиноренко Станислав. План:. Простейшие дифференциальные ...Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения. Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой ...Обыкновенные дифференциальные уравнения
Уравнение первого порядка. Функциональное уравнение F(x,y,y) = 0 или y= f(x,y), связывающее между собой независимую переменную, искомую функцию ...Дифференциальные уравнения второго порядка
y’’ = f(x,y,y’). y = (x,C’,C’’), Общее решение. где С’,С’’ - независимые постоянные,. Тогда начальные условия: у = у0 y/(х = х0) = y/0 tg 0 = y/0. ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0. 1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...Алгебраические уравнения произвольных степеней
Алгебраические уравнения произвольных степеней. 1. Введение. Всякий школьник, прежде всего, умеет решать уравнение первой степени: если дано уравнение ...Формула корней квадратного уравнения
Вы хотите научиться решать квадратные уравнения? ДА НЕТ. . . Содержание. Определение квадратного уравнения Дискриминант квадратного уравнения Формула ...График линейного уравнения с двумя переменными
Закончите предложение:. Линейным уравнением с двумя переменными называется уравнение вида. ах+by=с, где х и y – переменные, а, b и с – некоторые числа. ...Арксинус. Решение уравнения sin t = a
Цели. Изучить определение арксинуса числа. Изучить формулы решения простейшего тригонометрического уравнения sin t = a. Повторим. Что называется синусом ...Показательные уравнения и способы их решения
Определение: Показательные уравнения – уравнения, в которых переменная входит только в показатели степеней при постоянных основаниях. Например,. Основные ...Диофантовы уравнения
Цели и задачи. Определение диофантова уравнения Биография Диофанта Диофантовые уравнения первой степени Диофантовые уравнения высших степеней Проект ...Диофантовы уравнения
СКОЛЬКО РЕШЕНИЙ ИМЕЕТ ДАННОЕ УРАВНЕНИЕ? (2х+у)(5х+3у)=7. 3) Не имеет решений. 4) Бесконечно много решений. Следующее задание. (3х+7у)(х-у)=13 1) 2 ...Диофантовы уравнения
Диофантовы уравнения Глобально не изучаются в школьной программе, а присутствуют на экзамене! Проблема подтолкнувшая на создание работы:. обусловлена ...Диофантовы уравнения
Цели учебно – исследовательской работы: изучить способы решения диофантовых уравнений; повысить уровень математической культуры, прививая навыки самостоятельной ...Графическое решение линейного уравнения с двумя переменными
Цель урока:. проверить прочность знаний, умений и навыков, учащихся по данной теме, обеспечить закрепление и обобщение изученного материала; развивать ...Графики линейного уравнения с двумя переменными
Цель урока:. ввести понятие графика уравнения с двумя переменными; повторить построение графика линейной функции по двум точкам; закрепить навыки ...Показательные уравнения
Показательные. Цели урока: 1. ввести понятие показательных уравнений; 2. формировать умение решать показательные уравнения основными методами: функционально-графическим, ...Показательные уравнения
Математический диктант. Запишите функции. 1. Постройте схематично графики. 2. Выпишите убывающие функции 3. Для каждой из функций запишите множество ...Конспекты
Формула корней квадратного уравнения
Краткосрочное планирование по математике. Предмет. алгебра. Четверть. 1. Урок № 2 Класс. 8. . Дата 17.11.14г. . Тема урока. . ...Неравенства и уравнения, содержащие степень
Неравенства и уравнения, содержащие степень. Цель:. провести систематизацию и обобщение знаний по вопросам решения уравнений и неравенств; рассмотреть ...Тригонометрические уравнения
Тема урока «Тригонометрические уравнения» (2 часа). Тригонометрия по традиции занимает большое место в материалах конкурсных экзаменов в вузы; ...Уравнения и решения задач с помощью уравнения
Тема: «Уравнения и решение задач с помощью уравнений». 5 класс. Цель:. . закрепить умения и навыки решения уравнений и задач с помощью уравнений. ...Рациональные уравнения как математические модели реальных ситуаций
ПЛАН-КОНСПЕКТ УРОКА Рациональные уравнения как математические модели реальных ситуаций. . ФИО (полностью). . Науменкова Олеся Анатольевна. ...Свойства логарифмов. Логарифмические и показательные уравнения и неравенства
Муниципальное бюджетное образовательное учреждение. . «Средняя общеобразовательная школа № 7» им. О.Н. Мамченкова. . г. Елизово, Камчатский край. ...Дробные рациональные уравнения
Урок по алгебре в 9 классе. Тема урока:. Дробные рациональные уравнения. Цели урока:. 1) Организовать деятельность учащихся, способствующую формированию ...Показательные уравнения и неравенства
Технологическая карта урока по математике в 10 классе. по теме: «Показательные уравнения и неравенства». Учитель Бондарь Ирина Рувиновна. Предмет. ...Дробно-рациональные уравнения
РЕШЕНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ. Цели урока:. Обучающая:. формирование понятия дробно- рационального уравнения;. . рассмотреть различные ...Дробные рациональные уравнения
Тема урока:. «Дробные рациональные уравнения». Класс 9. Тип урока:. комбинированный. Цели: 1. . Образовательные:. Дать определение «дробно-рациональные ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:4 мая 2019
Категория:Математика
Содержит:45 слайд(ов)
Поделись с друзьями:
Скачать презентацию






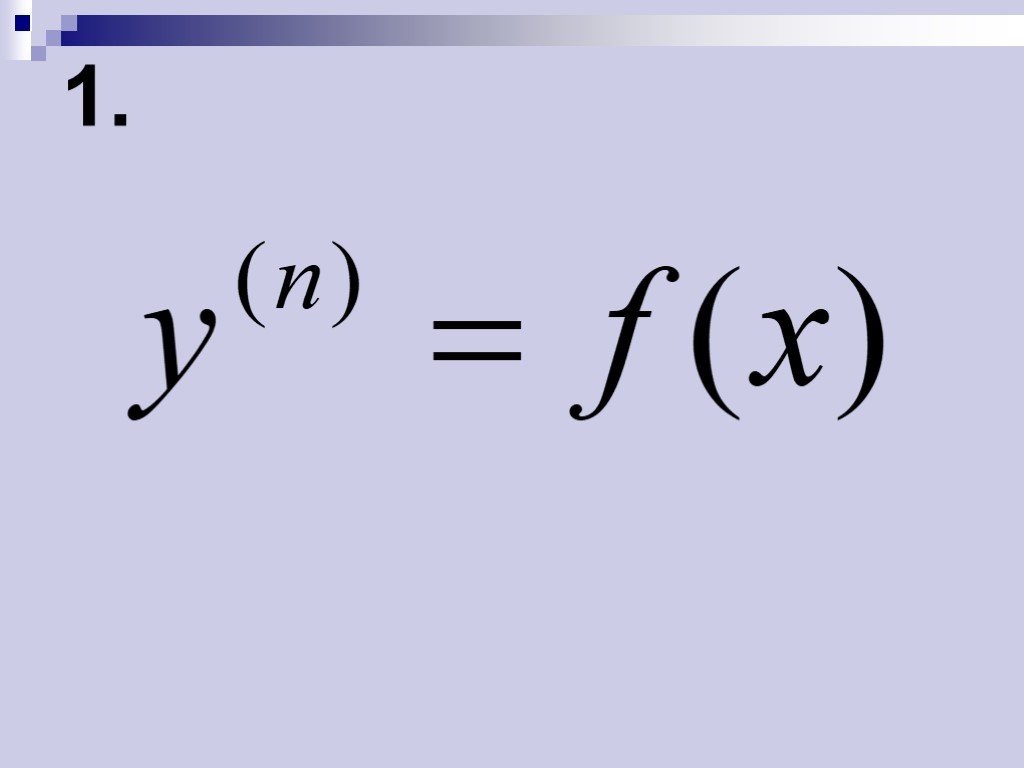












































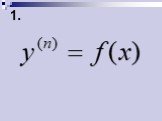





![Теорема. Пусть коэффициент , . Линейное дифференциальное уравнение непрерывно на некотором отрезке [a;b]. одно и только одно решение дифференциального уравнения, определенное и непрерывное на всем интервале (a;b), удовлетворяющее этому уравнению и любой системе начальных условий, если только значени Теорема. Пусть коэффициент , . Линейное дифференциальное уравнение непрерывно на некотором отрезке [a;b]. одно и только одно решение дифференциального уравнения, определенное и непрерывное на всем интервале (a;b), удовлетворяющее этому уравнению и любой системе начальных условий, если только значени](https://prezentacii.org/upload/cloud/19/05/145714/images/thumbs/screen12.jpg)









![Система функций определенных и непрерывных на отрезке [a;b] называется линейно зависимой на отрезке [a;b], если n таких чисел , что выполняется тождество , при этом (не все одновременно равны нулю) . Система функций определенных и непрерывных на отрезке [a;b] называется линейно зависимой на отрезке [a;b], если n таких чисел , что выполняется тождество , при этом (не все одновременно равны нулю) .](https://prezentacii.org/upload/cloud/19/05/145714/images/thumbs/screen22.jpg)





















































