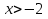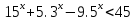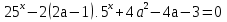Конспект урока «Показательные уравнения и неравенства» по математике для 10 класса
Технологическая карта урока по математике в 10 классе
по теме: «Показательные уравнения и неравенства». Учитель Бондарь Ирина Рувиновна.
| математика | Класс | 10 | |||||||||||
| Тема урока | Показательные уравнения и неравенства. | ||||||||||||
| Педагогические цели урока | Образовательная цель: закрепление и при необходимости коррекция и тренинг алгоритмов и способов решения показательных уравнений и неравенств. Деятельностная цель: формирование у учащихся способностей к рефлексии коррекционно-контрольного типа и реализации коррекционной нормы (фиксирование собственных затруднений, выявление их причин, построение и реализация проекта выхода из затруднений). Воспитательная цель: способствовать формированию ответственного отношения к учению, готовности и мобилизации усилий на выполнение заданий; воспитывать культуру учебного труда, навыков самоконтроля и экономного расходования времени; развивать коммуникативные навыки. | ||||||||||||
| Задачи урока |
| ||||||||||||
| Тип урока | Урок рефлексии. | ||||||||||||
| Планируемые образовательные результаты (с учетом разделов «Ученик научится», «Ученик получит возможность научиться») | |||||||||||||
| Предметные | Метапредметные | Личностные | |||||||||||
| Учащиеся научатся: решать показательные уравнения и неравенства базового уровня. Учащиеся получат возможность научиться: решать показательные уравнения и неравенства повышенного уровня. | Регулятивные: учащиеся научатся контролировать и корректировать свои действия при решении заданий базового уровня; прилагать волевые усилия в преодолении трудностей; Учащиеся получат возможность научиться планировать деятельность, направленную на решение заданий повышенной трудности. Познавательные: учащиеся научатся применять на практике знания алгоритмов решения показательных уравнений и неравенств; Учащиеся получат возможность научиться осуществлять творческую деятельность при решении заданий повышенного уровня сложности; выбирать наиболее эффективные способы решения. Коммуникативные: учащиеся научатся осуществлять взаимоконтроль, самоконтроль, прилагать волевые усилия в преодолении трудностей; Учащиеся получат возможность научиться выступать перед аудиторией, доказывать свою точку зрения на решение вопросов и толерантно относиться к мнению других учеников. | Ученик разовьет внимание, аккуратность, память, трудолюбие. Ученик получит возможность развития целеустремленности, интереса к учению, самовоспитанию. | |||||||||||
| Формы проведения урока | Фронтальный опрос, индивидуальная работа в системе голосования « Mimio Studio» , работа в группах (по три человека), самостоятельная работа дифференцированного характера. | ||||||||||||
| Педагогические технологии | Дифференцированное обучение. | ||||||||||||
| Оборудование и материалы | Доска, компьютер, проектор, экран, две самостоятельные работы в блокноте « Mimio Studio», карточки с заданиями для учащихся, работающих в группах, тексты дифференцированной самостоятельной работы, карточки с таблицей для рефлексии. | ||||||||||||
Структура урока.
| Деятельность учителя | Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов | Деятельность учеников | Планируемые результаты | ||||||||||||||||||||
| Предметные | УУД | ||||||||||||||||||||||
| Организует фронтальную беседу о теме, целях и плане урока. Показывает слайды с темой и целями урока (слайды смотреть в приложении). | Обдумать важность этого урока для дальнейшего успешного обучения и подготовки к контрольной работе и к ЕГЭ. Показ слайдов (смотреть в приложении).
| Записывают тему урока в тетрадь. Объясняют важность научиться решать показательные уравнения и неравенства для дальнейшего успешного обучения.
| Сформировать осознанный интерес к теме урока. Учащиеся получат возможность научиться целостно представить изучение темы. | Научатся обдумывать цель; осознать практическую и личностную значимость учебного материала. Учащиеся получат возможность научиться высказывать мнение. | |||||||||||||||||||
Цель: подготовка мышления учащихся и осознание ими потребности к выявлению причин затруднений при решении заданий базового уровня по теме урока. Продолжительность: 7минут. | |||||||||||||||||||||||
| Деятельность учителя | Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов | Деятельность учеников | Предметные | УУД | |||||||||||||||||||
| Организует самостоятельную работу с помощью ИКТ системы голосования « Mimio Studio»; организует самопроверку учащимися своих работ по ответам с фиксацией полученных результатов (без исправления ошибок). | Выполняют самостоятельную работу№1. (слайды смотреть в приложении). №1. А. – 0,5; В. – 1,5; С. 1,5 №2. А. х №3. А. 3; В. 4; С. -4 №4. А. С. | Решают самостоятельную работу №1 в виде теста в программе « Mimio Studio». После каждого задания показывается ответ; учащиеся сверяют результаты своей работы. | Научатся контролировать степень усвоения знаний, умений и навыков решения базовых показательных уравнений и неравенств. Учащиеся получат возможность научиться сформировать навыки успешно, точно, безошибочно и быстро выполнять решение заданий базового уровня. | Научатся осуществлять самоконтроль, прилагать волевые усилия в преодолении трудностей; Учащиеся получат возможность научиться активизировать соответствующие мыслительные операции и познавательные процессы(внимание, память и т.д.) | |||||||||||||||||||
Цель: осознание учащимися места и причины собственных затруднений в выполнении изученных ранее способов решения базовых показательных уравнений и неравенств; постановка цели и способов коррекционной деятельности; закрепление способов решения заданий, вызвавших затруднения. Продолжительность: 10 минут. | |||||||||||||||||||||||
| Деятельность учителя | Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов | Деятельность учеников | Предметные | УУД | |||||||||||||||||||
| Организует фронтальный опрос учеников для выявления затруднений и объяснения способов решения заданий, которые вызвали трудности, самопроверку учащихся по эталону. Учащиеся, которые выполнили работу без ошибок, получают карточки с дифференцирован- ными заданиями высокого и повышенного уровней. | Выявить и озвучить затруднения и объяснить способы решения заданий, которые вызвали трудности; исправить свои ошибки с помощью эталона (эталон смотрите в приложении). Задания для учащихся, которые не допустили ошибок, творческого характера более высокого уровня (на карточках), ученики выбирают по одному заданию своего варианта. (Карточки смотреть в приложении).
| Анализируют свои решения и определяют место ошибок; выявляют и фиксируют способы действий (алгоритмы, формулы, правила), в которых допущены ошибки. Ученики задают вопросы по решению заданий из работы №1; другие учащиеся объясняют способы решения этих заданий. Исправляют свои ошибки с помощью эталона. Остальные ученики решают дифференцированные задания по карточкам. | Научатся анализировать свои ошибки в решении заданий, формулировать, какие понятия и способы решения им надо научиться применять. Учащиеся, не допустившие ошибок, получат возможность научиться правильно выражать свои мысли в устной форме, развить творческие способности. | Научатся анализировать и сопоставлять результаты своей деятельности; ставить перед собой коррекционные цели; Учащиеся получат возможность научиться выступать перед аудиторий; преодолевать трудности. | |||||||||||||||||||
Цель: индивидуальная рефлексия достижения цели и создание (по возможности) ситуации успеха; закрепление знания способов решения показательных уравнений и неравенств. Продолжительность: 10 минут. | |||||||||||||||||||||||
| Деятельность учителя | Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов | Деятельность учеников | Предметные | УУД | |||||||||||||||||||
| Организация работы групп (по три человека) по решению заданий повышенного уровня сложности. Собирает самостоятельные работы творческого уровня. Организует самостоятельную работу с помощью ИКТ системы голосования « Mimio Studio»; организует самопроверку учащимися своих работ по эталону. | Учащиеся, набравшие 1, 2, 3 балла по самостоятельной работе №1, выполняют самостоятельную работу№2. (слайды смотреть в приложении). Учащиеся, набравшие 4 балла по самостоятельной работе №1, работают в группах по три человека, решая задания творческого характера. Работа №2 (базовая). №1. А. №2. А. 3; В. 4; С. 2 №3. А. Д. №4. А. Задания группам (по одному заданию каждой группе): №1. №2. №3. Найти все значения параметра а, при которых уравнение
имеет единственный корень. | Учащиеся, набравшие 1, 2, 3 балла по самостоятельной работе №1, решают самостоятельную работу №2 в виде теста в программе « Mimio Studio». После каждого задания показывается ответ; учащиеся сверяют результаты своей работы. Остальные ученики работают в творческих группах. | Научатся решать задания базового уровня по данной теме; контролировать степень усвоения знаний, умений и навыков решения; Учащиеся получат возможность научиться решать задания повышенного уровня по данной теме. | Научатся осуществлять самоконтроль, прилагать волевые усилия в преодолении трудностей; активизировать память, мышление, внимание. Учащиеся получат возможность научиться мыслить творчески, взаимодействовать в группе, учитывать мнение одноклассников, быть толерантным. | |||||||||||||||||||
Цель: закрепление изученных способов решения и применение знаний в новых ситуациях. Продолжительность: 10 минут. | |||||||||||||||||||||||
| Деятельность учителя | Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов | Деятельность учеников | Планируемые результаты | ||||||||||||||||||||
| Предметные | УУД | ||||||||||||||||||||||
| Проверяет результаты работы учеников в группах. Вызывает по каждому заданию одного ученика для отчета работы группы. | Объяснить у доски решение задания, которое разбирала группа. | Три ученика объясняют решение заданий, которые выполняла их группа, остальные могут задавать вопросы. | Ученики повторяют и закрепляют изученные способы решения заданий, знакомятся с применением их в новых ситуациях. Учащиеся получат возможность научиться решать задания повышенного уровня сложности; развить интерес к изучению математики. | Научатся строить аналогии, активизировать внимание и память, развивать в себе чувство долга, сознательную дисциплину и культуру поведения. Учащиеся получат возможность научиться обосновывать свою позицию, развивать речь и умение выступать перед аудиторией, умение объяснять. | |||||||||||||||||||
Цель: осознание учащимися метода преодоления затруднений и самооценка ими результатов своей деятельности на уроке; подведение итогов урока. Продолжительность: 5 минут. | |||||||||||||||||||||||
| Деятельность учителя | Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов | Деятельность учеников | Планируемые результаты
| ||||||||||||||||||||
| Предлагает учащимся проанализировать результаты работы на уроке; заполнить таблицу рефлексии; выбрать домашнее задание в соответствии с результатами деятельности на уроке (домашнее задание дифференцированное) Выставление отметок. Показ итогового слайда. | Проанализируйте результаты своей деятельности в соответствии с поставленной целью урока. Заполните таблицу рефлексии. Рефлексия.
В соответствии с результатами работы надо выбрать домашнее задание: Базовый уровень:№231(1,2),232(2),216(6). Высокий уровень: №226(1,4),225(3),238(1). Повышенный уровень: №227(2),226(2),225(2),239(3). ПО желанию можно выполнить дома задания из самостоятельной работы творческого уровня (на карточках была на уроке). | Анализируют свои успехи и деятельность на уроке. Заполняют таблицу рефлексии. Выбирают и записывают домашнее задание; по желанию берут карточку с работой домой. Смотрят итоговый слайд
| Научатся анализировать степень усвоения знаний, умений и навыков; в соответствии с результатами этого анализа научатся планировать свою учебную работу дома; Учащиеся получат возможность научится анализировать, прогнозировать и обобщать выводы о результатах своей работы; развить культуру самоуправления учением. | Научатся формировать навыки самоконтроля и анализа результатов работы; сознательно относиться к выбору домашнего задания; развивать культуру учебного труда. Учащиеся получат возможность развить способность мыслить критически; осуществлять самооценку и самокоррекцию учебной деятельности. | |||||||||||||||||||
Приложение.
Самостоятельная работа №1.
Самостоятельная работа №2.
Рефлексия.
-
С.р.
отметка
№1
№2
группа
итоговая
?
Самостоятельная работа повышенного уровня.
| Базовый уровень | Высокий уровень | Повышенный уровень | |
| 1 вариант |
Ответ: |
Ответ: -1 |
Ответ: (0;+ |
| 2 вариант |
Ответ: |
Ответ: -2 |
Ответ: (1;2) |
Задания для групп.
№1. 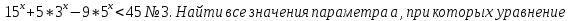
№2. 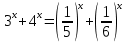
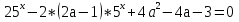 имеет единственный корень.
имеет единственный корень.
Слайды.



Разбор ошибок по эталону.
№1.
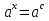
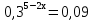
х=с
№2.
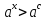
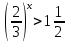
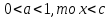
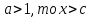
№3.
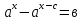
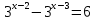
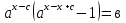
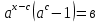
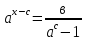
№4.
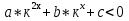
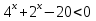
Замена: 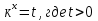
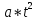 +b*t + c
+b*t + c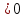
Список литературы.
-
Учебник «Алгебра и начала математического анализа» для 10-11 классов, Москва, «Просвещение», 2013г., авторы: Ш.А.Алимов, Ю.М.Колягин и др.
-
Учебник «Алгебра и начала математического анализа» для 10класса, Москва, «Просвещение», 2009г., авторы: С.М.Никольский, М.К.Потапов и др.
-
«Алгебра и начала математического анализа» для 10класса, дидактические материалы, Москва, «Просвещение», 2010г., авторы: М.И.Шабунин, М.В.Ткачева, Н.Е.Федорова, Р.Г.Газарян.
-
Учебник «Алгебра и начала математического анализа» для 10 класса, Москва, «Просвещение», 2010г., авторы: Ю.М.Колягин, М.В.Ткачева и др.
-
Учебно-методическое пособие «Алгебра и начала анализа» для 10-11 классов, Москва, «Дрофа», 2002г., автор П.И.Алтынов.
-
Тесты по алгебре и началам анализа для 10-11 классов, Санкт-Петербург, СМИО ПРЕСС, 2001г.
-
ФГОС основного общего образования, утвержден приказом Министерства образования и науки Российской Федерации от 17 декабря 2010г. №1897.
-
Стандарты второго поколения. Фундаментальное ядро содержания общего образования. Под редакцией В.В.Козлова, А.М.Кондакова, Москва, «Просвещение», 2009г.
-
Стандарты второго поколения. Примерная основная образовательная программа. Москва, «Просвещение», 2011г. Программа подготовлена институтом стратегических исследований в образовании РАО. Научные руководители — член-корреспондент РАО А. М. Кондаков, академик РАО Л. П. Кезина. Составитель — Е. С. Савинов.
Интернет – ресурсы:
-
Педсовет, математика http://pedsovet.su/load/135
-
Учительский портал. Математика http://www.uchportal.ru/load/28
-
Решу ЕГЭ
Здесь представлен конспект к уроку на тему «Показательные уравнения и неравенства», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.


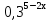 =0,09
=0,09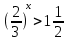
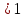 ; В.
; В.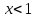 ; С.
; С. 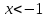 ; Д.
; Д.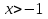
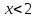 ; В.
; В. 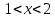 ;
;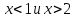 .
.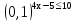
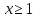
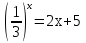
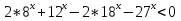
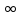 )
)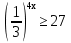
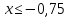
 ; В.
; В. 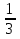 ; С.
; С. 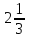
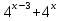 = 65
= 65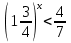
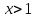 ;
;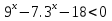
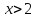 ; В.
; В. 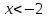 ; Д.
; Д.