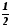Конспект урока «Формула корней квадратного уравнения» по математике для 8 класса
Краткосрочное планирование по математике
| Четверть 1 Урок № 2 Класс 8 Дата 17.11.14г | |||
| Тема урока | Формула корней квадратного уравнения | ||
| Ссылки | | ||
| Результаты обучения для учащихся | развивать способности учащихся к усвоению новой информации, формировать умение сравнивать, анализировать, кратко и четко выражать свое мнение | ||
| Основные идеи, отработанные по теме урока | Решение квадратных уравнений ax2 + bx + с = 0, где а ≠ 0 1. Найдем дискриминант (D) уравнения по формуле b2 – 4ac 2. Определим количество корней уравнения в зависимости от значения дискриминанта D D>0, уравнение имеет 2 корня; x1 = D= 0 уравнение имеет 1 корень ; x = D 3. Записать ответ Запись в тетради алгоритма решения квадратного уравнения, формулу корней квадратного уравнения. | ||
| Задания | время | Чем буду заниматься учитель | Чем буду заниматься ученики |
| 1. Мотивационный этап Эмоциональное Настроение, деление на группы | 3 мин | Учитель раздает цветные брелки и предлагает пройти к столам с таким же цветом | Делятся на группы и выбирают роли |
| 2.Актуализация знаний учащихся. | 7 мин | Фронтальная работа с классом (в это время 3 учащихся у доски работают по индивидуальным карточкам и целью контроля выполнения домашней работы (задания – аналогичны дом. заданию). | 3-е учащихся работают по индивидуальным карточкам, а остальные отвечают на вопросы |
| | | - Что такое уравнение? Что такое корень уравнения? Что значит решить уравнение? - Какие уравнения мы называем линейными? Какие уравнения мы называем квадратными? Приведите примеры - Сколько корней может иметь линейное уравнение (квадратное) уравнение? Примеры. - Какие виды неполных квадратных уравнений вам известны? Приведите примеры. - Какой общий вид имеет полное квадратное уравнение? Приведите пример. Какие квадратные уравнения мы с Вами умеем решать? | |
| 3. Первичное усвоения новых знаний ( презентация) | 7мин | Вывести формулу корней квадратного уравнения (на доске) Ввести понятие дискриминанта квадратного уравнения (Приложение 1, слайд 4) Рассмотреть различные случаи решения квадратного уравнения в зависимости от значения дискриминанта (D) (Приложение 1 слайды 5-8) Решение квадратных уравнений ax2 + bx + с = 0, где а ≠ 0 1. Найдем дискриминант (D) уравнения по формуле b2 – 4ac 2. Определим количество корней уравнения в зависимости от значения дискриминанта D D>0, уравнение имеет 2 корня; x1 = D= 0 уравнение имеет 1 корень ; x = D 3. Записать ответ Запись в тетради алгоритма решения квадратного уравнения, формулу корней квадратного уравнения. | Учащиеся далают запись в тетради алгоритма решения квадратного уравнения, формулу корней квадратного уравнения. |
| 4. Физкультминутка (включить спокойную музыку) (Приложение 1, слайд 9, приложение 2 – музыка) | 1 мин | Выполняют танцевальные движения | Выполняют танцевальные движения |
| 5.Первичная проверка понимания Работа в группах | 10 мин | x2 = Ответ: - 0,2; 1 Пример 2 4x2 - 12x + 9 = 0 а = 4, b = - 12, с = 9 D = b2 – 4ac = (-12)2 – 4 ∙ 4 ∙ 9 = 144 - 144 = 0, D = 0, уравнение имеет 1 корень x = Ответ: 1,5 Пример 3 7x2 + 3x + 5 = 0 а =7, b = 3, с = 5 D = b2 – 4ac = (-3)2 – 4 ∙ 7 ∙ 5 = 9 - 140 = 131, D Ответ: нет корней Пример 4 2х2 + 3х +1 =0 Ответ: -1, - | Учащиеся изготовляют постеры на решение примеров |
| 6. Первичное закрепление Работа на уроке. | | Решение квадартных уравнений (работа в парах) Приложение 2 (4 варианта) 1 пара
2. x² - 4x + 4 = 0 3 пара 1. 3x² + 4x + 20 = 0 2. 5x²- 3x - 2 = 0 4 пара 1. х2 – 15х + 14 = 0; 2. 9 – 2х2 – 3х = 0; | Учащиеся работают в парах |
| 7. Домашнее задание | | Выполнить № 129,№130 | |
| 8. Итог урока Рефлексия. Выставление оценок учащимся | | Рефлексия (Приложение 1, слайд
| Учащиеся посчитывают баллы, полученные за урок |
Здесь представлен конспект к уроку на тему «Формула корней квадратного уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

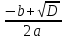 ,
, 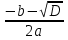
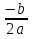
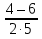 = - 0,2
= - 0,2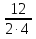 = 1,5
= 1,5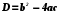 = 32 – 4∙2∙1 = 9 – 8 = 1 > 0
= 32 – 4∙2∙1 = 9 – 8 = 1 > 0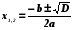 =
= 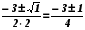
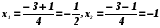 .
.