Конспект урока «Геометрическая прогрессия. Формула n-го члена геометрической прогрессии» по математике для 9 класса

Открытый урок в 9 классе МБОУСОШ станицы Терской.

Учитель Яшина Н.П.

Тема урока: «Геометрическая прогрессия. Формула n-го члена геометрической прогрессии».

Цель урока:

-дать представление о геометрической прогрессии и вывести формулу n-го члена ГП;

-формировать умение применять данную формулу при решении задач;

-воспитывать ответственное отношение к своим поступкам, продумывать их последствия;

- вырабатывать умение составлять план и последовательность действий для достижения цели, владеть монологической и диалогической формами речи в соответствии с нормами родного языка.

Оборудование: проектор, компьютерная презентация, учебник.

Тип урока: освоение нового материала.

Метод обучения: деятельностный, проблемный, частично-поисковый.

Формы организации познавательной деятельности: фронтальная, индивидуальная.

План урока.

1.Мотивация (самоопределение) к учебной деятельности (организационный момент).

2.Актуализация знаний и фиксирование индивидуального затруднения в проблемном действии (повторение изученного материала, необходимого для «открытия нового знания»).

2.1 Повторение изученного материала

а) фронтальная работа с классом

б) решение задачи №614 (устно)

2.2 Проблемная ситуация

2.3 Закрепление полученных знаний.

3. Выявление места и причины затруднения в новой проблемной ситуации.

4. Построение проекта выхода из затруднения.

5. Первичное закрепление

а) во внешней речи

б) закрепление материала в процессе решения задачи

6. Самостоятельная работа с самопроверкой по эталону.

7. Включение нового материала в систему знаний.

8. Задача для любознательных.

9. Рефлексия деятельности (итог урока)

10. Домашнее задание.

Развёрнутый конспект урока.

Слайд 1. (Урок алгебры в 9 классе)

Ход урока.

1.Мотивация (самоопределение) к учебной деятельности (организационный момент).

Слайд 2. Здравствуйте, ребята. Цель нашего урока, как и любого другого я бы определила в виде формулы трёх П: Познакомиться. Понять. Применять.

Если в конце урока мы сможем сказать, что познакомились с новой темой, поняли её и научились применять полученные знания на практике, значит, наша цель будет достигнута.

2.Актуализация знаний и фиксирование индивидуального затруднения в проблемном действии (повторение изученного материала, необходимого для «открытия нового знания»).

2.1 Повторение изученного материала

а) фронтальная работа с классом

Прежде, чем приступить к изучению нового материала, повторим предыдущую тему. Итак, как называется тема, над которой мы работали на предыдущих уроках? (Арифметическая прогрессия)

Слайд 3. –Дайте определение арифметической прогрессии.

-Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.

-А как называется это одно и то же число? (Разность арифметической прогрессии)

Докажите, что представленные последовательности чисел являются арифметическими прогрессиями . (На слайде появляются три числовые последовательности, дети отвечают)

-А какое свойство этих последовательностей не только доказывает, что это прогрессии, но и объясняет их название – арифметические прогрессии? (Каждый член этих последовательностей равен среднему арифметическому предыдущего и последующего членов)

Учащиеся доказывают сказанное примером.

Примерный ответ ученика с использованием формулы ПОПС:

П (позиция) Я думаю, что эта последовательность - арифметическая прогрессия.

О (обоснование) Каждый её член равен среднему арифметическому предыдущего и последующего членов.

П (пример).Например: 12 – это среднее арифметическое чисел 9 и 15 : (9+15)/2=12.

С (следствие)Следовательно, это арифметическая прогрессия.

Слайд 4.- Определите, какие из этих рисунков иллюстрируют арифметическую прогрессию, укажите разность каждой прогрессии.

-Что можно вычислить, зная только первый член прогрессии и её разность (n –ый член прогрессии и сумму n первых членов прогрессии). Назовите эти формулы.

Слайд 5. С именем какого математика связывают формулу суммы n первых членов АП? (Карла Гаусса, немецкого математика, которого впоследствии называли королём математики).

Слайд 6.

а)Повторяем формулу n-го члена АП и формулу суммы нескольких первых членов.

б) Решение задачи №614 (устно) с использованием второй формулы суммы n первых членов АП.

При свободном падении тело прошло в первую секунду 5м, а в каждую следующую на 10м больше. Найдите глубину шахты, если тело достигло её дна через 5с после начала движения

Решение .

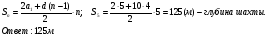
2.2 Проблемная ситуация.

Слайд 7.

Ещё раз обратимся к рисункам. Найдите рисунок, иллюстрирующий арифметическую прогрессию. Докажите. Рассмотрим другие рисунки и выясним, как изменяется каждый последующий член относительно предыдущего. Иллюстрируют ли эти рисунки какую-то последовательность, или это случайный набор чисел? (Да). Какую? (Дети могут сказать, что это последовательность геометрическая, т.к. прочитали об этом в учебнике).- Да, верно, но почему эта последовательность называется геометрической , а не, скажем, алгебраической или тригонометрической? Обоснуйте свой ответ по формуле ПОПС.

Слайд 8. (Дети должны сказать, что каждый член этой последовательности равен среднему геометрическому предыдущего и последующего членов).

Итак, как мы можем определить тему нашего урока? (Геометрическая прогрессия). Попробуем дать определение геометрической прогрессии , опираясь на определение арифметической прогрессии.

(Все вместе дети формулируют определение)

Геометрической последовательностью называется последовательность отличных от нуля чисел, каждый член которой равен предыдущему, умноженному на одно и то же число.

-Вспомните, как называется это одно и то же число в арифметической прогрессии. (Разность АП). А в ГП это одно и то же число называется знаменателем ГП. Он обозначается латинской буквой q

Определите разность ГП на этих рисунках.

Слайд 9.

-А теперь сравним две прогрессии по этой схеме. (Объясняем, что у обеих прогрессий можно назвать первый и любой последующий член, в АП- разность, в ГП – знаменатель, числа, которые показывают, как изменяется последующий член по сравнению с предыдущим).

2.3 Закрепление полученных сведений. Решить устно №623 а,б.

3. Выявление места и причины затруднения в новой проблемной ситуации.

Предлагаю решить такую старинную задачу.

Слайд 10.

Один мужик на рынке заключил с купцом договор на месяц. Мужик предложил купцу, что будет приносить ему каждый день по 100 рублей, а купец при этом должен будет в 1-ый день дать ему 1 копейку, во второй- 2коп., в 3-ий – 4коп. и так каждый день удваивать сумму взноса. Образованный купец пришёл домой и всё рассказал жене. Жена сожалела о том, что договор заключён только на месяц.

-Какой вопрос мы могли бы поставить в этой задаче?

-Итак, сколько же денег по договору даст купец мужику в первый день спора? Во 2-ой? В 3-ий? Что представляет собой изменение этой суммы? (Сумма растёт в геометрической прогрессии)

-Можете ли вы мне дать ответ в течении минуты, сколько денег должен дать купец на, предположим, 11-ый день спора? (Нет, не хватит времени). А как можно посчитать быстрее? Каких знаний нам не хватает, чтобы ответить на этот вопрос? (Нужно знать формулу n-го члена ГП) Вот это и будет продолжением нашей темы. Записываем в тетрадь со справочными материалами.

Слайд 11.

Тема: «Геометрическая прогрессия. Формула n-го члена ГП»

4. Построение проекта выхода из затруднения.

-Какие у вас идеи? Если бы мы не знали, сколько денег купец даст в 1-ый день, могли бы мы узнать что-то про 2-ой, 3-ий день? (Нет). Значит, нам нужно знать 1-ый член ГП, т.е. b₁. Что ещё мы должны знать? (Как должна изменяться сумма, т.е., знаменатель ГП -q).

Дети записывают в тетрадь, один ученик делает вывод формулы у доски.

Дано: b₁, q

Найти: b_n

b₂=b₁*q; b₃= b₂*q= b₁*q*q= b₁q²; b₄= b₃*q= b₁q²*q= b₁q³

……………………………………………………………………………………………………………………………

Формула в общем виде: b_n=b₁*q^n-1

Итак, мы вывели формулу n-го члена ГП. Используя её, скажите формулу для 5-го, 11-го, 31-го члена ГП.

Сравните её с формулой n-го члена АП.

Если в формуле n-го члена АП сложение заменить умножением, а умножение возведением в степень, то мы получим формулу n-го члена ГП.

5.Первичное закрепление

а) во внешней речи

Переведите эту формулу с языка математики на русский язык, т.е., скажите её словами. Проговорим формулу хором, повторите её друг другу в парах.

б) Закрепление материала в процессе решения задачи.

-Теперь, используя формулу, мы сможем посчитать, сколько денег даст купец мужику на 11-й день договора.

Решим эту задачу.

Дано:

b₁=1; q=2

Найти: b₁₁

Решение.

b₁₁=b₁*q¹⁰; b₁₁=1*2¹⁰=1*1024=1024=10руб.24коп.

Ответ:10руб.24коп.

Конечно, нам интереснее узнать, кто выиграет в этом споре. Предлагаю вам дома посчитать, сколько денег должен отдать купец мужику на 31 день договора, а сколько всего он будет должен мужику, это уже тема следующих уроков.

6. Самостоятельная работа с самопроверкой по эталону.

Слайд 14.

Решить самостоятельно №625а,б, проверить по эталону. Разбирается характер ошибок.

Слайд 15, 16

7. Включение нового материала в систему знаний.

Решить с комментированием у доски № 627б, 630а.

8. Задача для любознательных.

Прочитайте задачу и попробуйте дать ответ

• Некогда был пруд, в центре которого рос один лист лилии. Каждый день число таких листьев удваивалось, и на десятый день вся поверхность пруда была заполнена листьями лилий. Сколько понадобилось дней, чтобы заполнить лилиями половину пруда?

• (5дней, 9 дней, 8 дней)

9. Рефлексия деятельности (итог урока)

-Что узнали на этом уроке? Удалось ли нам реализовать поставленную цель? Оцените по 5-бальной системе своё участие в уроке.

10. Домашнее задание.

• На «3»: № 627, 628.

• На «4»: № 627, 628, 630.

• На «5»: № 627, 628, 630, 631.

• Удачи вам, ребята!

• Спасибо за урок!