Конспект урока «Сумма n-первых членов геометрической прогрессии» по математике для 9 класса
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
| Логунова Лариса Владимировна | |
| Предмет: | Алгебра |
| Класс: | 9 |
| Тема урока: | «Сумма n-первых членов геометрической прогрессии» |
| Тип урока: | Открытие новых знаний |
| Цель: | Формирование понятия суммы n-первых членов геометрической прогрессии. Отработка на практике навыков применения формулы суммы n-первых членов геометрической прогрессии. |
| Планируемые результаты | Предметные: решают задачи на нахождения суммы n-первых членов геометрической прогрессии, прогнозируют результат вычислений. Находят и выбирают удобный способ решения заданий. Личностные: выражают положительное отношения к процессу познания; применяют правила делового сотрудничества; осознают границы собственного знания и «незнания»; оценивают свою учебную деятельность. Метапредметные: Регулятивные – определяют цель учебной деятельности, осуществляют поиск средств её достижения, обнаруживают и формулируют учебную проблему совместно с учителем. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи, записывают выводы в таблицу. Коммуникативные – умеют слушать других, принять другую точку зрения, изменить свою точку зрения |
| Технологии: | Информационно-коммуникационные технологии; Технология развития «критического мышления»; |
| Оборудование: | Компьютер, мультимедийный проектор, экран, презентация в программе PowerPoint, индивидуальный раздаточный материал для учащихся (карточки с заданиями). |
| Используемые приемы | Верите ли Вы, Инсерт. |
| Литература | О.В.Занина, И.Н.Данкова Поурочные разработки по алгебре к учебному комплекту А.Г.Мордковича 9 кл. – М.: ВАКО. 2007, - 496с (В помощь школьному учителю) С.И.Заир-Бек Развитие критического мышления на уроке: пособие для учителей общеобразоват. учреждений / М.: Просвещение, 2011, - 223с. Ю.Н. Макарычев, Н.Г. Миндюк. К.И. Нешков, с. Б Суворова ; под ред. С.А. Теляковского. Алгебра. Учебник для 9 кл. общеобразовательных учреждений. Москва. «Просвещение» 2011 г. Лысенко Ф. Ф. Алгебра 9кл. Итоговая аттестация. Ростов-на-Дону. Издательство «Легион» 2012,2013г. |
КОНСПЕКТ УРОКА
Система действий учителя и ученика
| Действия учителя | Действия ученика | |
| 1 | 2 | 3 |
| Орг.момент 2 мин. | 1. Проверяет готовность учащихся к уроку 2. Предлагает с помощью карточек показать свое настроение | 1.Готовятся к уроку 2. С помощью карточек демонстрирует свое настроение |
| Вызов 7 мин. | 1. Начинает урок с небольшого вступления и сообщает учащимся о том, как будет построен урок (слайд №1,2,3) 2. Предлагает учащимся заполнить карточку с вопросами. Все они начинаются со слов «Верите ли вы, что», Ответ на вопрос может быть только: «Да» или «Нет» (Приложение 1). 3. После окончания работы выслушав мнение учащихся, заполняет первую строчку сводной таблице на доске | 1.Участвуют в беседе 2. Заполняют первый столбик карточки. Если «Да», то с право от вопроса они ставят знак «+» если нет, знак «-» 3. Участвуют с помощью сигнальных карт в заполнении таблице |
| Осмысление 2 мин. | 1. Подводя итоги работы с вопросами таблицы, готовит учеников к мысли, что, отвечая на вопросы, мы пока не знаем, правы или нет, так как мнения разделились | 1. Участвуют в обсуждении |
| Рефлексия 3 мин. 5 мин. | 1. Предлагает в течении трех минут посмотреть свои записи и обменятся информацией в парах 2. Демонстрирует презентацию, (слайды 4-12) | 1. Обсуждают в парах ответы на вопросы, по необходимости обращаются к учебнику. Заполняют второй столбик таблицы «+» или «-» 2. Участвуют в обсуждении и заполняют третью строчку таблицы |
| Повторный вызов 4 мин. | 1. Предлагает проанализировать выполненную работы и ответить вопрос: какие моменты связанные с прогрессиями не были рассмотрены в презентации.(слайд 13) 2. Дома вы должны прочитать параграф 28 до примера 1 и карандашом на полях расставить значки «+» - уже знал, «?» - не понял, «!» - не знал, но узнал и понял, Ү | 1. Участвуют в обсуждении. 2. Открывают учебники, где на полях расставлены значки |
| Осмысление 3 мин. | 1. Предлагает учащимся проанализировать проделанную дома работу. Снимает возникшие затруднения 2. На доске появляются формулы суммы n – первых членов геометрической прогрессии. (Слайды 14-15) | 1.Участвуют в обсуждении 2.Записывают в конспект формулы, заполняют таблицу. |
| Рефлексия 9 мин. | 1.Предлагает практические задания на основе изучаемой информации а) знакомит учащихся с индийской легендой об изобретателе шахмат.(видео). На доске записывает решение задачи (слайд 16-17), б) предлагает решить задачу прогрессии в биологии (слайд 19 ), в) предлагает учащимся решить задачи по теме геометрическая прогрессия по теме из открытого банка математических задач ГИА 2013 (слайд 20-21) г) предлагает решить задачу на расчет процентов по вкладам (слайд 22). | 1.Используют знания, полученные на стадии осмысления при решении задач. а) оформляют в тетрадях рассмотренную задачу. б) обсуждают решение в парах. в) решают в тетрадях самостоятельно, демонстрируют на доске. г) совместно с учителем решают задачу |
| Итоговая рефлексия 3 мин. | Предлагает заполнить памятку для учащихся «рефлексия урока» (слайд 23)
| Заполняют памятку рефлексия урока |
| Домашнее задание 2 мин. | Задает домашние задание 1. Параграф 27-28 2. Тест по теме прогрессия (Приложение 1) 3. Подготовить презентацию по теме: «Прогрессии в банковском деле» | Записывают домашнее задание в дневник, задание 3 для желающих |
Приложение 1.
Вопросы: Верите ли вы что. . . .
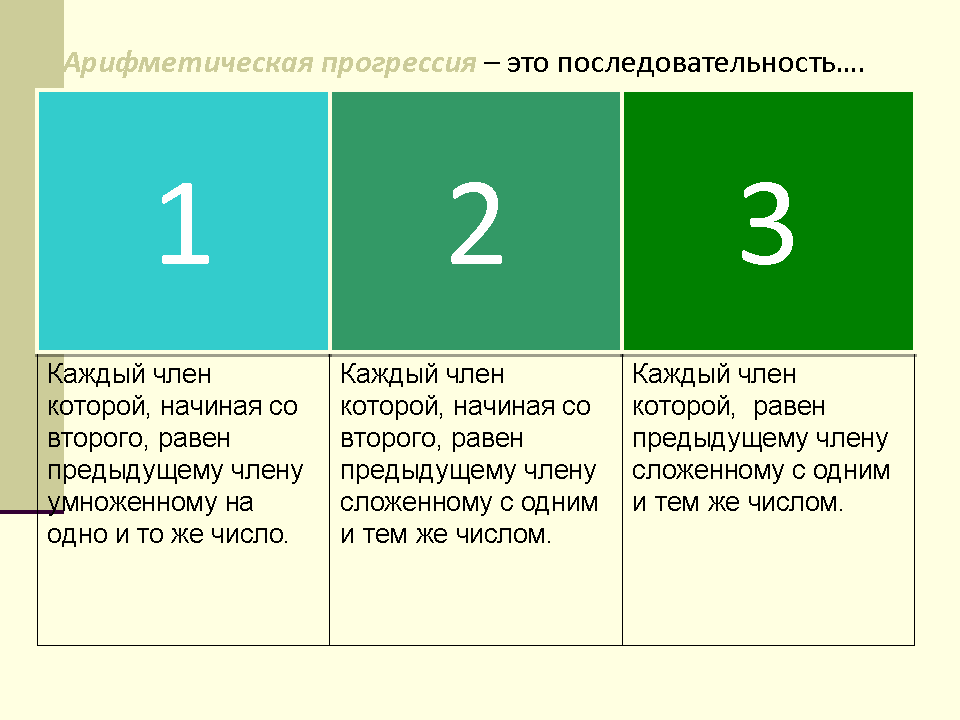
| Арифметическая прогрессия – это последовательность, каждый член которой, равен предыдущему члену, сложенному с одним и тем же членом | | | | |
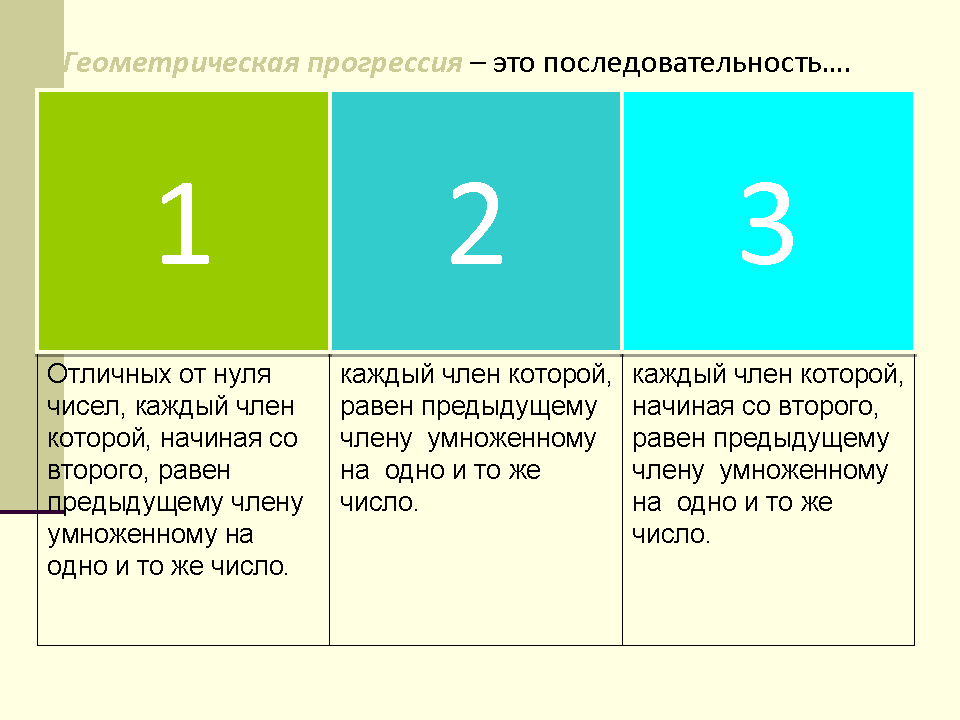
| 2 | Геометрическая прогрессия – это последовательность каждый член которой, начиная со второго, равен предыдущему члену умноженному на одно и то же число | | | |
| 3 | Формула для нахождения разности арифметической прогрессии d = an + 1 - an | | | |
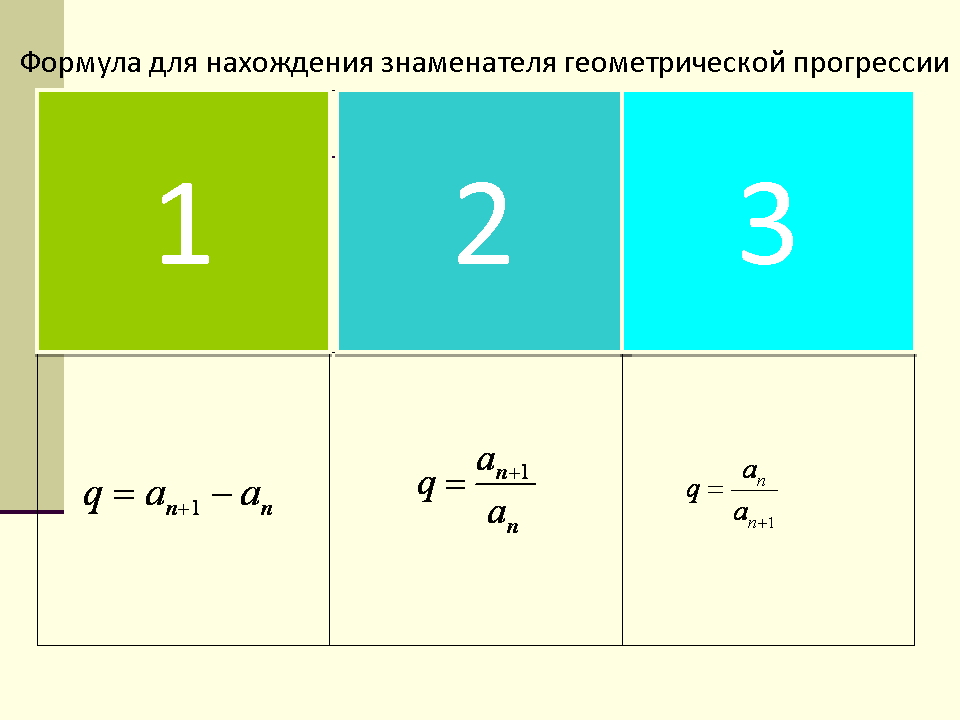
| 4 | Формула для нахождения знаменателя геометрической прогрессии an q = ------- an + 1 | | | |
| 5 | Формула для нахождения n – го члена арифметической прогрессии an = a1 - d*(n - 1) | | | |
| 6 | Формула для нахождения n – го члена геометрической прогрессии an = a1 · qn - 1 | | | |
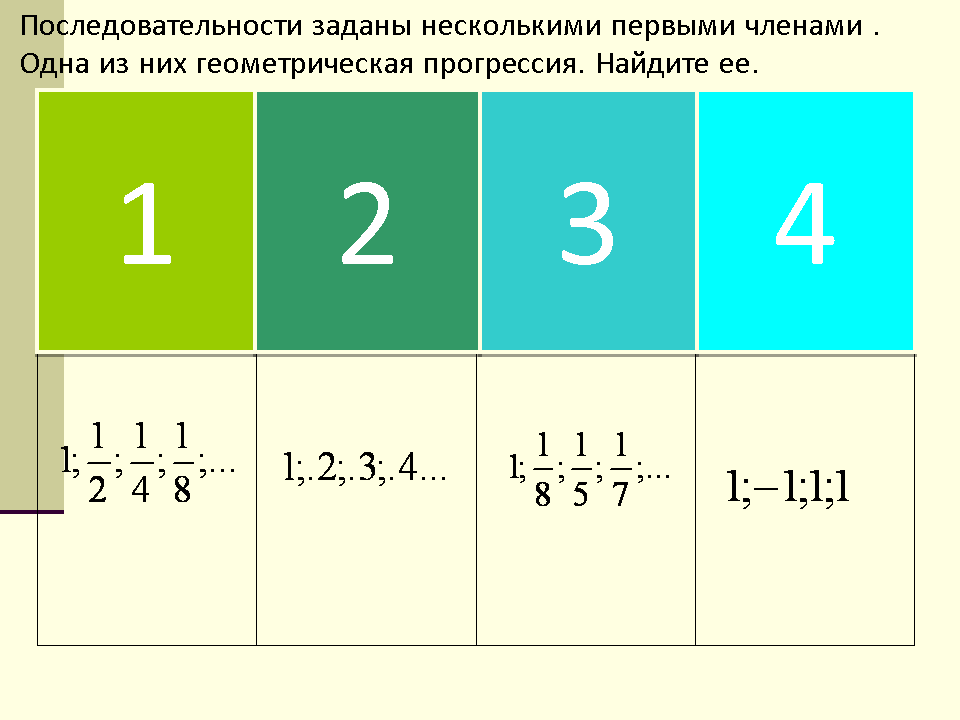
| 7 | Последовательности заданы несколькими первыми членами. Среди них нет геометрической. прогрессии a) 1; 1 ; 1 ; 1 в) 1; 1 ; 1 ; 1 2 4 8 8 5 7 б) 1; 2 ; 3 : 4: г) 1; - 1; 1; 1; | | | |
| 8 | Что если, арифметическая прогрессия ( вn ) задана условиями в1 = 4 вn +1 = вn +5 то в2 = 9 | | | |
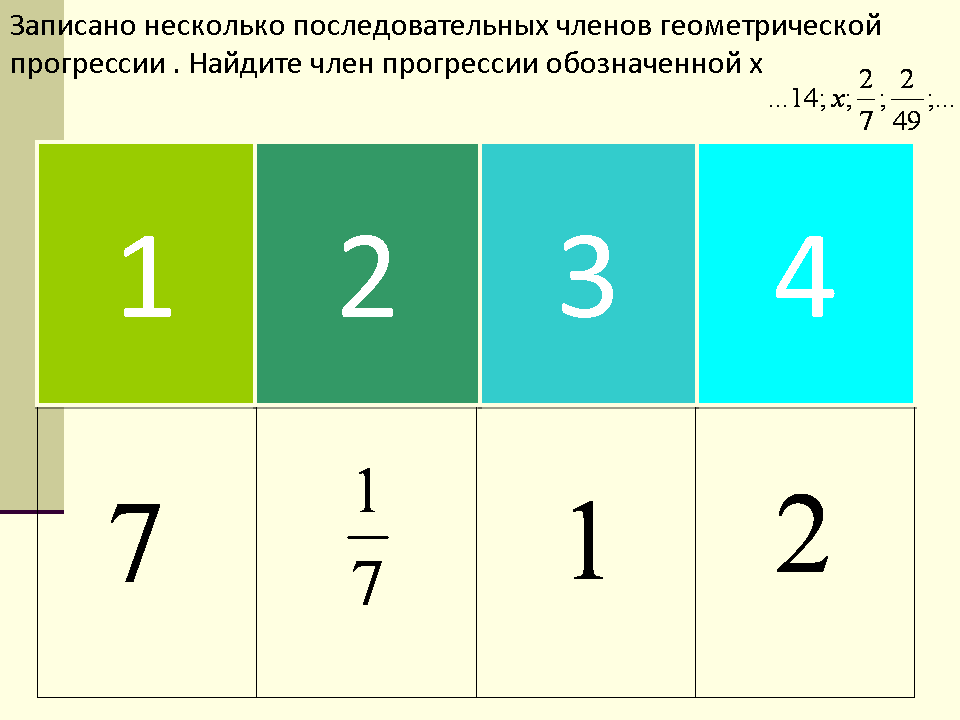
| 9 | Что если (вn) – геометрическая прогрессия, то член прогрессии обозначенный буквой x = 2 …14; Х; 2 ; 2 7 49 | | | |
Домашнее задание
_ _________________________________________________________________
_________________________________________________________________
Рефлексия урока
-
За что ты можешь себя похвалить…………….
-
Что приобрел …………………………………..
-
Осталась проблема…………………………….
-
Где можно применить полученные знания…….
-
Сегодня на уроке я научился……………………
-
Оценка за урок………………………………….
Приложение 2.

Слайд 1.

Слайд 2.

Слайд 3.
Слайд 4.
Слайд 5.

Слайд 6.
Слайд 7.

Слайд 8.
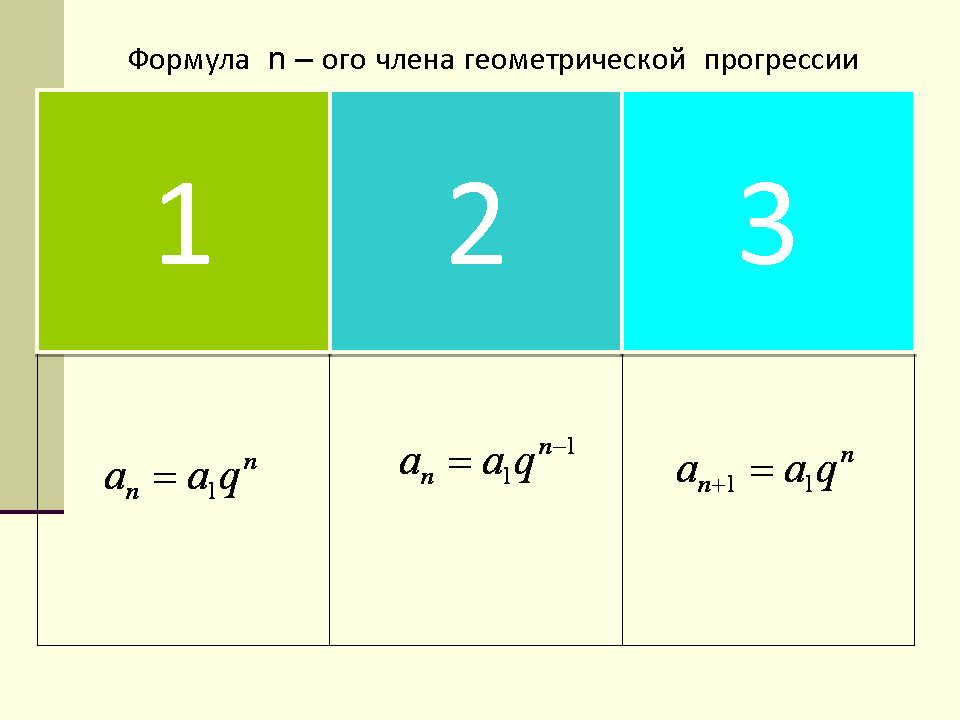
Слайд 9.
Слайд 10.

Слайд 11.
Слайд 12.

Слайд 13.

Слайд 14.

Слайд 15.

Слайд 16.

Слайд 17.

Слайд 18.

Слайд 19.

Слайд 20.

Bn=3n-2
Слайд 21.

Слайд 22.

Слайд 23.

Слайд 24.
Здесь представлен конспект к уроку на тему «Сумма n-первых членов геометрической прогрессии», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

