Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии.

Скажи мне, и я забуду.
Покажи мне, и я запомню.
Вовлеки меня, и я научусь.
Китайская мудрость.

Тип урока: урок ознакомления с новым материалом c использованием мультимедиа.

Цели урока:

• Ввести понятие об арифметической прогрессии как числовой последовательности особого вида;

• Вывести формулу n-го члена арифметической прогрессии;

• Формировать умения применять формулу n-го члена арифметической прогрессии.

• Развивать логическое мышление.

Задачи урока:

• Воспитательная – воспитывать настойчивость в учебе, умение слушать, ответственное отношение к учебному труду.

• Учебная – совершенствовать знания о последовательностях.

• Развивающая – развивать познавательный интерес, мышление, память, внимание.

Оборудование:

• Мультимедиа проектор;

• Цветной мел;

• Проверочный тест;

Ход урока

I.Проверка домашнего задания

Девизом нашего урока является высказывание: « Скажи мне, и я забуду. Покажи мне, и я запомню. Вовлеки меня, и я научусь».

Сегодня на уроке вы сами сможете вывести формулу n-го члена арифметической прогрессии.

Начнем с проверки домашнего задания:

№ 565, № 568( у доски 2 ученика), остальные работают устно:

1. В последовательности (х_п): 2; 0; -2; -4…. назвать первый , второй, третий, пятый, шестой члены.

2. Последовательность у_п задана формулой n-го члена у_n= 5n + 1. Найти у₁, у_4, у₂₀, у_100, у_k.

3. Найти второй, пятый, двадцатый члены последовательности (а_п), заданной формулой:

А) а_n = 2n – 1; Б) а_n = ;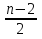

4. Последовательность задана формулой а_n = 15 - 3n. Найти номер члена последовательности, равного 6; 0; -3.

5. Последовательность задана формулой а_n= 2 - 3n. Является ли членом этой последовательности число -12; 3.

6. Найти среднее арифметическое чисел 2 и 10; 3 и – 5 ; 3 и 7.

II.Объяснение нового:

выпишите последовательность, соответствующую условию задачи:

1. Джентльмен получил наследство. В первый месяц он истратил 100$, а каждый следующий месяц он тратил на 50$ больше, чем в предыдущий.

2. Мастерская изготовила в январе 100 изделий, а в каждый следующий месяц изготовляла на 12 изделий больше, чем в предыдущий.

3. Тело в первую секунду движения прошло 2 м, а за каждую следующую секунду – на 3 м меньше, чем за предыдущую.

Каким образом образовались члены данных последовательностей?

Выписанные последовательности являются арифметическими прогрессиями.

Сформулируйте определение арифметической прогрессии.

( можно обратиться за помощью к учебнику стр. 141 § 25 )

Задайте данные последовательности рекуррентным способом.

( а₁ = 100, а_n+1 = а_n + 50; а₁= 100, а_n+1 = а_n + 12; а₁ = 27, а_n+1 = а_n -3)

Вывод: последовательность (а_n) - арифметическая прогрессия, если для любого натурального n выполняется условие а_n+1 = а_n + d, где d – некоторое число, называемое разностью арифметической прогрессии.

Т.е. d = а_n+1 - а_n

Рекуррентный способ задания арифметической прогрессии не очень удобен ( почему? ), поэтому необходимо получить формулу n –го члена.

Предлагается самостоятельно вывести формулу n -го члена.

( используя рекуррентный способ задания последовательности)

а_n = а₁ + (n – 1) d

III.

• Найти разность арифметической прогрессии

(а_n): 1; 2; 3; 4…..

( у_n) : -2; -4; - 6….

• (а_n) – арифметическая прогрессия. а₁ = -2, d = 3. Найти а₄; а₆; а₁₀.

Почему данная последовательность получила название арифметическая прогрессия?

1. Найти среднее арифметическое чисел 2 и 10.

2. Запишите в порядке возрастания полученное число с данными. (2; 6; 10;14; 18;22…)

3. Образует ли данная тройка чисел арифметическую прогрессию?

4. Проверьте выполняется ли данная закономерность для любой тройки чисел этой последовательности.

5. Сформулируйте свойство членов арифметической прогрессии.

( каждый член арифметической прогрессии, начиная со второго равен среднему арифметическому предыдущего и последующего членов ).

Полученное свойство является характеристическим свойством арифметической прогрессии.

6. Как вы считаете верно ли обратное утверждение?

Если в последовательности (а_n) каждый член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то эта последовательность является арифметической прогрессией.

Доказать.

IY. Применение знаний в стандартной ситуации.

№ 575 (а, б) – самостоятельно с самопроверкой.

№ 576 ( а,в,д) – работа у доски.

№ 578 – комментирование.

Тестирование

Вариант № 1

Сдать тест, проверить с помощью слайда.

Y. Итог урока

Оцените «уровень успешности»: Нарисуйте на полях кружок - если вам все было понятно и вы справились; квадрат – если кое-что непонятно и треугольник – если все непонятно и срочно нужна помощь.

YI. Домашнее задание

№ 575(в,г), №581, № 583 § 25