Конспект урока «Формулы корней квадратного уравнения» по математике для 8 класса
Открытый урок по алгебре
«Формулы корней
квадратного уравнения»
8 класс
Подготовила и провела:
учитель математики
Моисеевской ООШ
Штетингер С.Ю.
Тема: Формулы корней квадратного уравнения
Цель: повторение и закрепление умений и навыков решения квадратных уравнений
Задачи:
-
Способствовать формированию умений применять на практике полученные знания
-
Развивать логическое мышление, память, внимание, математическую речь
-
Воспитывать активность, трудолюбие, взаимоуважение
Тип урока: урок систематизации и обобщения знаний
Методы обучения: наглядные, практические, самостоятельна работа.
Оборудование: интерактивная доска, презентация, раздаточный материал
Ход урока.
-
Организационно-мотивационный момент.
-
Психологический настрой:
Добрый день! Добрый час!
Я очень рада видеть вас.
Прозвенел уже звонок
Начинается урок.
Улыбнулись, подтянулись
Друг на друга посмотрели
И тихонько дружно сели.
-
Постановка целей и задач урока.
Не всегда уравненья
Решают без сомненья
Даже когда квадрат
Стоит над уравненьем
Но итогом сомненья
Может быть озаренье.
- Ребята, скажите, пожалуйста, на какую мысль вас наводят строки этого стихотворения? (услышали слова «уравнение», «квадрат», «решают»)
- Хорошо. Над чем мы сегодня с вами будем работать? (над уравнением, над квадратным уравнением)
- Какие цели необходимо поставить перед собой? (повторить и закрепить умения решать квадратные уравнения)
- Каждый из вас имеет получить оценку за урок по результатам работы на различных этапах. Для этого у вас на партах лежат карты результативности, в которые вы будете фиксировать свои успехи. Для ответа на поставленный вопрос вы поднимаете руку и ни в коем случае не перебиваете друг друга. Желаю всем удачи.
Карта результативности.
| Разминка | Тест | Реш. уравн | «Найди ошибку» | Сам. работа | ИТОГО | Дополнит задан | |
| | |||||||
| Кол-во баллов | | | | | | | |
-
Актуализация опорных знаний.
-
Разминка ( каждый правильный ответ 2 балл).
-
Какое название имеет уравнение второй степени?
(уравнение второй степени называется квадратным уравнением)
-
Сформулируйте определение квадратного уравнения.
(уравнение вида ах2+bx+c=0, где а, b и с – любые действительные числа, причем а≠ 0, х – переменная, называется квадратным уравнением)
-
Перечислите виды квадратных уравнений. (полные, неполные, приведенные)
-
От чего зависит количество корней квадратного уравнения? (кол-во корней квадратного уравнения зависит от дискриминанта D)
-
Сколько корней имеет квадратное уравнение, если D больше 0? (при D > 0, уравнение имеет два корня)
-
Сколько корней имеет квадратное уравнение, если дискриминант меньше 0 (при D )
-
Какое квадратное уравнение называется приведенным? (квадратное уравнение называется приведенным если а = 1 и имеет вид х2 + рх + q = 0).
-
Есть у любого слова, у растения и может быть у уравнения? (корень)
-
Формулы корней квадратного уравнения?
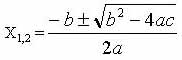 или
или ![]()
-
Тест “Виды квадратных уравнений”
| полное | неполное | приведенное | Общий балл | |
| 1) х4 + 5х2 +3 = 0 | | | | |
| 2) 6х2 + 9 = 0 | | | | |
| 3) х2 – 3х = 0 | | | | |
| 4) –х2 + 2х +4 = 0 | | | | |
| 5) 3х + 6х2 + 7 =0 | | | | |
Ребята выполняют работу, а затем меняются листочками и по ключу проверяют ответы, оценивая работу товарища. Результат записывается в колонку “Оценочный балл”, а затем в “Карту результативности”( каждый правильный ответ 1 балл).
| + | | + | |
| 2 | | + | |
| 3 | | + | + |
| 4 | + | | |
| 5 | + | | |
Ключ к тесту:
- Молодцы. С видами квадратных уравнений мы разобрались. Кстати, а вы знаете, когда появились первые квадратные уравнения?
Историческая справка
Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными, относятся во второму тысячелетию до н.э. Это эпоха расцвета Вавилона и Древнего Египта.
Квадратные уравнения впервые встречаются в работе индийского математика и астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в) изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения. И лишь в 17 веке, благодаря Ньютону, Декарту и другим ученым, эти формулы приняли современный вид.
- Ребята, а с каким еще понятием мы постоянно сталкиваемся при решении квадратных уравнений? (С дискриминантом)
- А вот понятие Д придумал английский ученый Сильвестр, он называл себя даже “математическим Адамом” за множество придуманных терминов. А зачем он нам нужен?(Он определяет число корней квадратного уравнения)
- И как количество корней зависит от D?(Дети перечисляют случаи:
Если D
Если D> 0, то уравнение имеет два корня
Если D=0, то уравнение имеет два одинаковых действительных корня (ли один)
- Итак, давайте еще раз проговорим алгоритм решения полного квадратного уравнения.
(Проговаривают.
АЛГОРИТМ
-
Выделить в квадратном уравнении коэффициенты.
2. Вычислить дискриминант D.
3. Если D
Если D>или=0, то вычислить корни по формуле.
![]()
-
Работа по теме урока.
- Ну что ж, приступим к практической части нашего урока.
1) Устный счёт
√4 = 42 = (-82) =
(-1)2 = √64= √144 =
√25 = √100 = 72 =
(-3)3 = (-2)3 = √49 =
√169= √400= √1 =
-
Решение уравнений
Чтобы решить уравнение,
Корни его отыскать.
Нужно немного терпения,
Ручку, перо и тетрадь.
- Перед вами список различных уравнений. Посмотрите внимательно на уравнения 1-3 и скажите: являются ли эти уравнения квадратными? (Да. Потому что наивысшая степень 2)
- А что вас смущает во внешнем виде этих уравнений? (Они записаны не в стандартном виде)
Итак, преобразуйте данные уравнения к стандартному виду и найдите корни уравнения. (каждый правильный ответ 1 балл)
| Ответы: 1. 5х2 + х - 6 = 0 | |
| 2. 4х – 5 + x2 = 0 | 2. х2 + 4х - 5 = 0 |
| 3. (2 - 5х)2 = 9 | 3. 25х2 – 20х – 5 = 0 |
Проверка.
| 2. x2 + 4х - 5 = 0, х1 = -5 х2 = 1 |
25х2 – 20х – 5 = 0 Х1 = -0,2 х2 = 1 |
-
«Найди ошибку»
- Представьте себе, что вы учитель. Исправьте допущенную ошибку в решении уравнения (за правильное исправление 1 балл)
| х2 – 10х + 16 = 0 D = b2 – 4ac = (-10)2 – 4* 16 = 100 – 64= 49, 49> 0 Х1 = Х 2 = |
Физминутка.- А теперь немного отдохнём.
Быстро встали, улыбнулись
Выше-выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Глубоко вдохнули.
Спину потянули,
Руки вверх подняли
Радугу нарисовали
Повернулись на восток,
Продолжаем наш урок.
-
Самостоятельная работа.
- Хорошо. Вместе мы поработали. Теперь посмотрим, как вы умеете работать самостоятельно. Вам предлагается трехуровневая работа.
Если вы еще не уверены в своих силах и желаете закрепить решение уравнение, то выбираете уровень А (3 балла).
Если считаете, что материал усвоен хорошо – В (6 баллов).
Ну, а если желаете испробовать свои силы на более сложных заданиях – уровень С (10 баллов) для вас.
В процессе решения я проверяю ваши работы и проставляю заработанные баллы.
Вариант 1.
Уровень А.
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 3х2 + 6х – 6 = 0, б) х2 - 4х + 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 - 7х + 2 = 0, D = b2 - 4ac = (-7)2 – 4· 5 · 2 = …;
№3. Закончите решение уравнения 3х2 - 5х – 2 = 0.
D = b2 - 4ac = (-5)2- 4· 3·(-2) = 49; х1 = … х2=…
Уровень В. Решите уравнение: а) 6х2 – 4х + 32 = 0; б) х2 + 5х - 6 = 0.
Уровень С. Решите уравнение: (3х - 1)(х + 3) = х + 6х2
Вариант 2.
Уровень А.
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 4х2 - 8х + 6 = 0, б) х2 + 2х - 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 + 8х - 4 = 0, D = b2 - 4ac = 82 – 4· 5 · (- 4) = …;
№3. Закончите решение уравнения х2 - 6х + 5 = 0.
D = b2 - 4ac = (-6 )2 - 4· 1·5 = 16; х1 = … х2=…
Уровень В. Решите уравнение: а) 3х2 – 2х + 16 = 0; б) 3х2 - 5х + 2 = 0.
Уровень С. Решите уравнение: (х +4)2 = 3х +40
Дополнительные задания (каждый правильный ответ 1 балл)
Тест.
-
Найти дискриминант уравнения
-
2у2+3у+1=0
А) 11; Б) 17; В)-5; Г)1
-
2у2+5у+2=0.
А) 41; Б) 9; В)-11; Г) 21
-
х2-6х+5=0
А) 16; Б) -56 В)-16; Г)56
-
х2-7х+12=0
А) -1; Б) -97 В)1; Г) 97
-
Сколько корней имеет уравнение?
-
х2-9х+14=0
А) два; Б) один В)не имеет корней Г)множество
-
х2-8х+15=0
А) два; Б) один В)не имеет корней Г) множество
-
2х2+х+2=0
А) два; Б) один В)не имеет корней Г) множество
-
Зх2+х+4=0
А) два; Б) один В)не имеет корней Г) множество
Ответы:
-
1. Г 2.Б 3. А 4. В
-
1. А 2. А 3. В 4. В
-
Поведение итогов
- Итак, мы проделали большую работу. Повторили всю теорию, касающуюся полных квадратных уравнений. Решали различные их виды как вместе.
Вы старательно зарабатывали баллы, настало время подвести итог.
Подсчитайте сумму баллов заработанных в течение урока.
Критерии оценки
-
22 – 27 баллов
«5»
14 – 21 балл
«4»
6 – 13 баллов
«3»
-
5 балла
«2»
Дополнительное задание
За 10 прав. ответов
«5»
За 7-9
«4»
За 5-6
«3»
-
Выставляются оценки.
VII. Рефлексия.
Чем лично для вас был интересен этот урок?
- Какие формы работы вам понравились?
- На каком этапе урока вы испытывали затруднения?
- Как вы думаете, над какими вопросами данной темы предстоит еще поработать?
-
Домашнее задание.
Карточки
Задание достаточного уровня:
1) х2 + 2х – 80 = 0;
2) 4х2 + 4х + 1 = 0;
3) 3у2 – 3у + 1 = 0.
Задание высокого уровня:
1) 5х2 = 9х + 2;
2) (х + 4 )2 = 3х + 40;
3) (3х – 1)(х + 3) =х(1 + 6х).
«Найди ошибку»
(за правильное исправление 1 балл)
| х2 – 10х + 16 = 0 D = b2 – 4ac = (-10)2 – 4* 16 = 100 – 64= 49, 49> 0 Х1 = Х 2 = |
«Найди ошибку»
(за правильное исправление 1 балл)
| х2 – 10х + 16 = 0 D = b2 – 4ac = (-10)2 – 4* 16 = 100 – 64= 49, 49> 0 Х1 = Х 2 = |
«Найди ошибку»
(за правильное исправление 1 балл)
| х2 – 10х + 16 = 0 D = b2 – 4ac = (-10)2 – 4* 16 = 100 – 64= 49, 49> 0 Х1 = Х 2 = |
| Решение и ответы: | |
| |
| |
| Решение и ответы: | |
| |
| |
| полное | неполное | приведенное | Общий балл | |
| 1) х4 + 5х2 +3 = 0 | | | | |
| 2) 6х2 + 9 = 0 | | | | |
| 3) х2 – 3х = 0 | | | | |
| 4) –х2 + 2х +4 = 0 | | | | |
| 5) 3х + 6х2 + 7 =0 | | | | |
| полное | неполное | приведенное | Общий балл | |
| 1) х4 + 5х2 +3 = 0 | | | | |
| 2) 6х2 + 9 = 0 | | | | |
| 3) х2 – 3х = 0 | | | | |
| 4) –х2 + 2х +4 = 0 | | | | |
| 5) 3х + 6х2 + 7 =0 | | | | |
| полное | неполное | приведенное | Общий балл | |
| 1) х4 + 5х2 +3 = 0 | | | | |
| 2) 6х2 + 9 = 0 | | | | |
| 3) х2 – 3х = 0 | | | | |
| 4) –х2 + 2х +4 = 0 | | | | |
| 5) 3х + 6х2 + 7 =0 | | | | |
| полное | неполное | приведенное | Общий балл | |
| 1) х4 + 5х2 +3 = 0 | | | | |
| 2) 6х2 + 9 = 0 | | | | |
| 3) х2 – 3х = 0 | | | | |
| 4) –х2 + 2х +4 = 0 | | | | |
| 5) 3х + 6х2 + 7 =0 | | | | |
| полное | неполное | приведенное | Общий балл | |
| 1) х4 + 5х2 +3 = 0 | | | | |
| 2) 6х2 + 9 = 0 | | | | |
| 3) х2 – 3х = 0 | | | | |
| 4) –х2 + 2х +4 = 0 | | | | |
| 5) 3х + 6х2 + 7 =0 | | | | |
Карта результативности.
| Разминка | Тест | Реш. уравн | «Найди ошибку» | Сам. работа | ИТОГО | Дополнит задан | |
| | |||||||
| Кол-во баллов | | | | | | | |
Карта результативности.
| Разминка | Тест | Реш. уравн | «Найди ошибку» | Сам. работа | ИТОГО | Дополнит задан | |
| | |||||||
| Кол-во баллов | | | | | | | |
Карта результативности.
| Разминка | Тест | Реш. уравн | «Найди ошибку» | Сам. работа | ИТОГО | Дополнит задан | |
| | |||||||
| Кол-во баллов | | | | | | | |
Карта результативности.
| Разминка | Тест | Реш. уравн | «Найди ошибку» | Сам. работа | ИТОГО | Дополнит задан | |
| | |||||||
| Кол-во баллов | | | | | | | |
Карта результативности.
| Разминка | Тест | Реш. уравн | «Найди ошибку» | Сам. работа | ИТОГО | Дополнит задан | |
| | |||||||
| Кол-во баллов | | | | | | | |
Дополнительные задания
(каждый правильный ответ 1 балл)
Тест.
-
Найти дискриминант уравнения
-
2у2+3у+1=0
А) 11; Б) 17; В)-5; Г)1
-
2у2+5у+2=0.
А) 41; Б) 9; В)-11; Г) 21
-
х2-6х+5=0
А) 16; Б) -56 В)-16; Г)56
-
х2-7х+12=0
А) -1; Б) -97 В)1; Г) 97
-
Сколько корней имеет уравнение?
-
х2-9х+14=0
А) два; Б) один В)не имеет корней Г)множество
-
х2-8х+15=0
А) два; Б) один В)не имеет корней Г) множество
-
2х2+х+2=0
А) два; Б) один В)не имеет корней Г) множество
-
Зх2+х+4=0
А) два; Б) один В)не имеет корней Г) множество
Здесь представлен конспект к уроку на тему «Формулы корней квадратного уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

 =
= 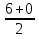 =
= 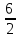 = 8
= 8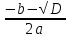 =
= 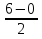 = 2
= 2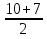 =
= 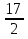 = 8
= 8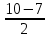 = 2
= 2