Конспект урока «Искусство составлять уравнения» по математике для 6 класса
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №20 города Йошкар - Олы»
Искусство составлять уравнения
(урок математики в 6 классе)
Подготовила и провела:
учитель математики
Шишкарёва
Светлана
Михайловна
г.Йошкар – Ола
2012 г.
Цель:
Развитие и совершенствование умений составлять уравнения.
Задачи:
-
Показать, что умение составлять уравнения сводится к умению переводить «с родного языка на алгебраический».
-
Познакомить с нестандартными задачами, решаемых алгебраическим способом.
-
Развивать математическое мышление, грамотную математическую речь, интерес к математике.
-
Воспитывать уважительное отношение друг к другу, взаимопонимание, уверенность в себе.
Оборудование: интерактивная доска, персональный компьютер, презентация.
Ход урока
Орг. момент.
Вступительное слово учителя. (Слайд 1)
«Мне приходится делить время между политикой и уравнениями. Однако уравнения, по – моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Альберт Эйнштейн
Учитель. Ребята, как вы думаете, о чём сегодня на уроке будет идти речь?
Ответы обучающихся.
Учитель. Итак, сегодня на уроке мы должны выяснить, в чём состоит искусство составлять уравнения. (Слайд 2)
Предлагаю вам решить следующую задачу. (Слайд 3)
(Один ученик решает у доски, остальные в тетрадях.)
Я задумал число, умножил его на 5, а затем из произведения вычел 2,7. В результате получил – 21,7. Какое число я задумал? (Ответ: -3,8)
Учитель. С помощью чего мы решили задачу?
Ответы обучающихся.
Учитель. Действительно, мы решили задачу с помощью уравнения.
В математике данный способ называется алгебраическим, а раздел математики, предметом изучения которого являются уравнения, называется алгебра. (Слайд 4)
Учитель. Проведём блиц – опрос.
Блиц – опрос.
-
Какое равенство называют уравнением?
-
Как называют значение буквы, при котором из уравнения получается верное числовое равенство?
-
Что значит решить уравнение?
Ответы на блиц – опрос. (Слайд 4)
Уравнением называют равенство, содержащее букву, значение которой надо найти.
Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения.
Решить уравнение, значит найти все его корни или убедиться, что это уравнение не имеет ни одного корня.
Учитель. Устно решим уравнения. (Слайд 5)
(Один ученик на интерактивной доске расставляет стрелки от уравнения к его решению, остальные проверяют.)
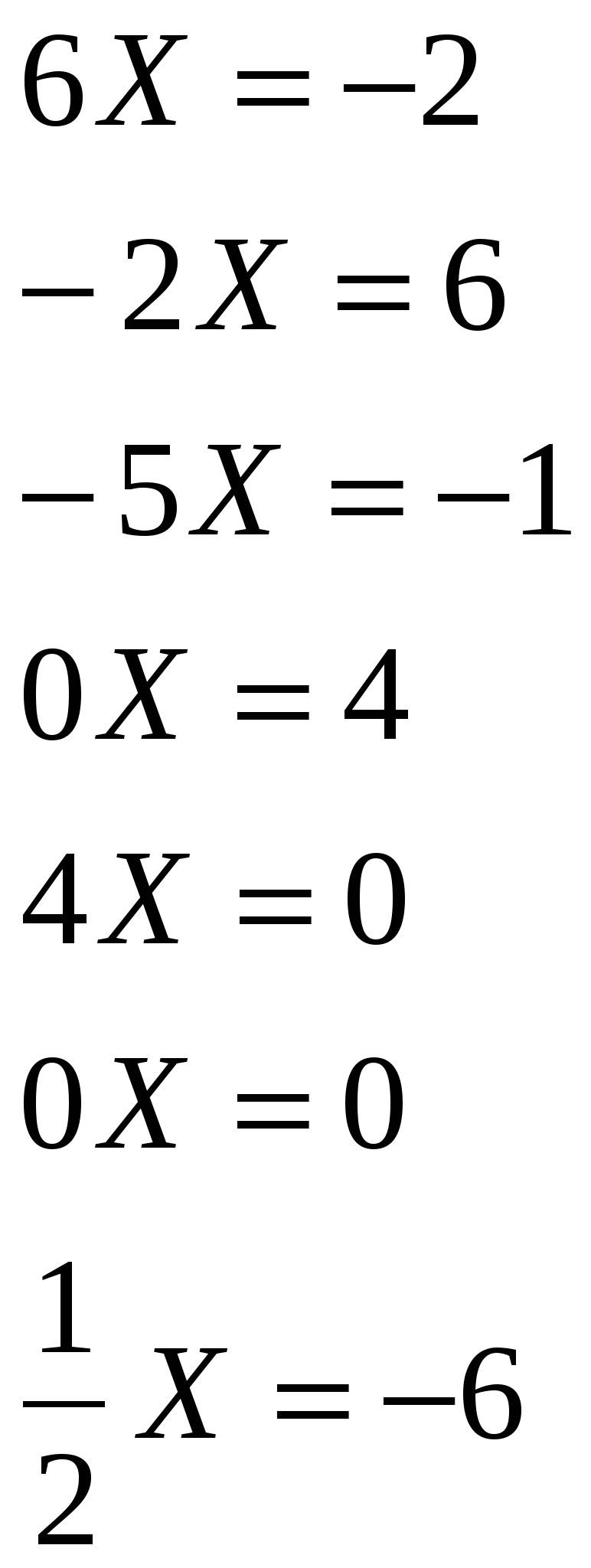
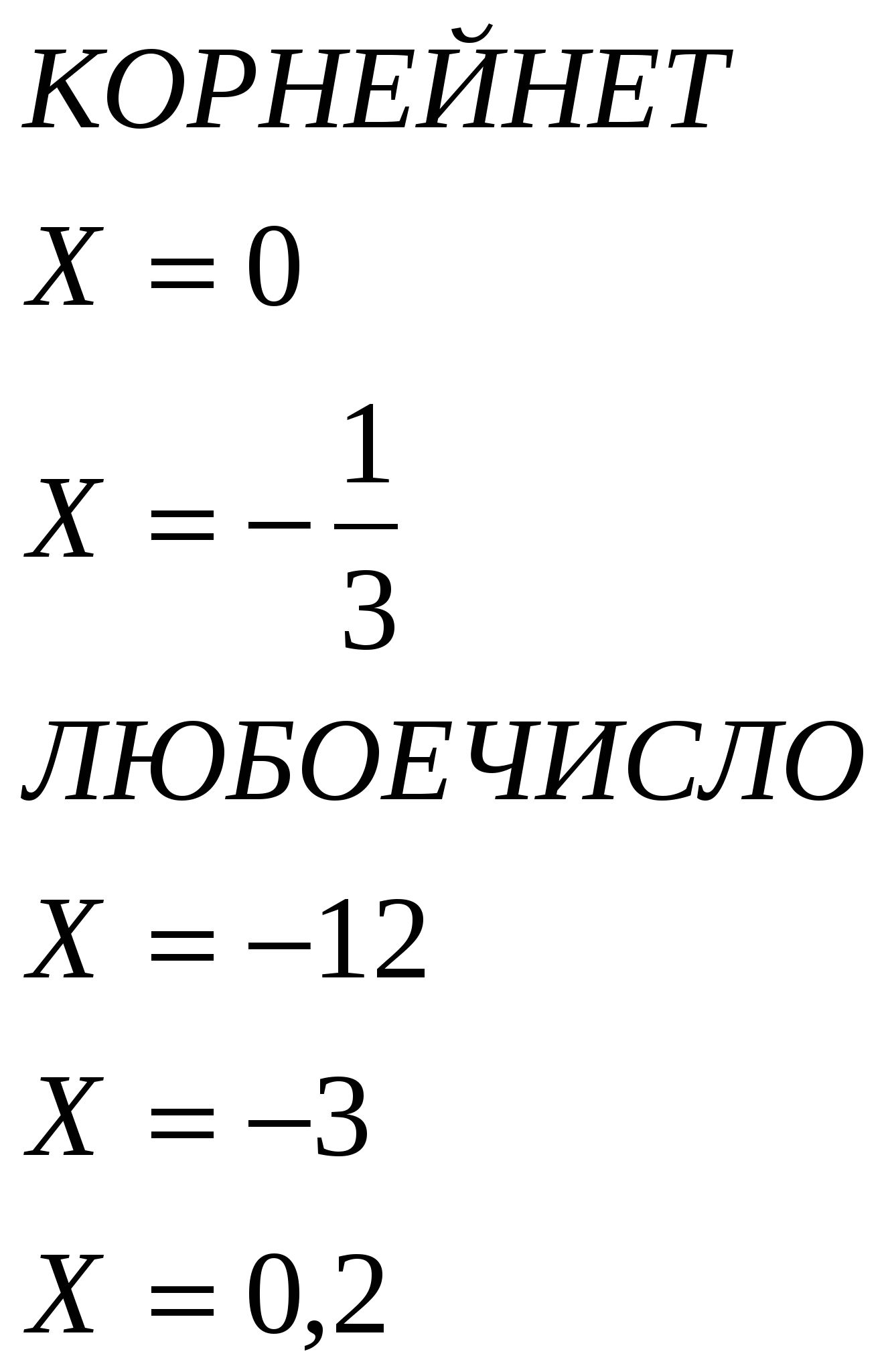 Уравнения Ответы
Уравнения Ответы
Учитель. (Слайд 6)
« Чтобы решить вопрос, относящийся к числам или к отвлечённым отношениям величин, нужно лишь перевести задачу с родного языка на язык алгебраический», - писал великий Ньютон в своём учебнике алгебры, озаглавленном «Всеобщая арифметика».
Как именно выполняется такой перевод с родного языка на алгебраический, Ньютон показал на примерах в своём учебнике. Вот один из них.
| На языке алгебры | |
| Купец имел некоторую сумму денег. |
|
| В первый год он истратил 100 фунтов. |
|
| К оставшейся сумме добавил третью её часть. |
|
| В следующем году он вновь истратил 100 футов. |
|
| И увеличил оставшуюся сумму на третью её часть. |
|
| В третьем году он опять истратил 100 фунтов. |
|
| После того как он добавил к остатку третью его часть, |
|
| капитал его стал вдвое больше первоначального. |
|
Чтобы определить первоначальный капитал купца, остаётся только решить последнее уравнение. Учиться решать подобные уравнения нам предстоит в дальнейшем.
Сейчас поупражняемся в переводе с родного языка на алгебраический, решая несложные задачи.
Задача 2. (Слайд 8)
Каков возраст братьев? (Задача из книги, изданной в XVII веке после «Арифметики» Л.Ф. Магницкого)
Средний из трёх братьев старше младшего на два года, а возраст старшего брата превышает сумму лет двух остальных братьев четырьмя годами. Найти возраст каждого брата, если вместе им 96 лет. (Ответ: старшему – 50лет, среднему – 24 года, младшему - 22 года.)
Задача 3. (Слайд 9)
Античные этюды (Пифагор Самосский, около 580 – 501г.г. до н.э.)
Поликрат однажды спросил на пиру у Пифагора, сколько у того учеников. «Охотно скажу тебе, о Поликрат, - отвечает Пифагор. – Половина моих учеников изучает прекрасную математику. Четверть исследует тайны вечной природы. Седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь ещё к ним трёх юношей, из которых Теон превосходит прочих своими способностями. Сколько учеников веду я к рождению вечной истины». Сколько учеников было у Пифагора? (Ответ: 28 учеников.)
Учитель. А сейчас, я выступлю в роли фокусника. Предлагаю вашему вниманию «фокус» по отгадыванию чисел. Каждому из вас, надо задумать число от 1 до 20, затем выполнить действия, представленные в таблице. (Слайд 10)
(Обучающиеся работают в тетрадях.)
Учитель. Теперь назовите свой результат, а я сообщу задуманное вами число.
Учитель. В чём секрет «фокуса»?
Ответы обучающихся.
Учитель. Секрет, разумеется, очень прост, и в основе его лежат все те же уравнения.
Итак, заполним правую колонку таблицы. (Слайд 10)
(Один ученик работает на интерактивной доске, остальные в тетрадях.)
| На языке алгебры | |
| Задумай число, | х |
| прибавь 2, | х+2 |
| умножь результат на 3, | (х+2)·3 = 3х+6 |
| отними 5, | (3х+6) – 5 = 3х+1 |
| отними задуманное число, | (3х+1) – х = 2х+1 |
| умножь на 2, | (2х+1)·2 = 4х+2 |
| отними 1. | (4х+2) – 1 = 4х+1 |
Учитель. Из правой колонки видно, что если вы задумали какое – то число х, то после всех действий у вас должно получиться 4х+1.Зная это, нетрудно «отгадать» задуманное число.
Например, после выполнения всех действий получилось 61. Теперь предстоит решить в уме уравнение 4х+1 = 61. В результате находим: х = 15. Это и есть задуманное число.
Как видите, всё очень просто: фокусник заранее знает, что надо сделать с результатом, чтобы получить задуманное число.
Сейчас, каждый из вас составит и решит своё уравнение.
Учитель. Немного поупражнявшись, вы легко сможете сами показывать своим приятелям такие «фокусы».
Решение уравнений – зачастую дело нетрудное; составление уравнений по данным задачи затрудняет больше.
Подведение итогов.
Учитель. Итак, в чём же состоит искусство составлять уравнения?
Ответы обучающихся.
Учитель. Вы видели сейчас, что искусство составлять уравнения действительно сводится к умению переводить «с родного языка на алгебраический». Но язык алгебры весьма немногословен; поэтому перевести на него удаётся без труда далеко не каждый оборот родной речи.
В дальнейшем, мы продолжим работу по составлению и решению уравнений.
Домашнее задание. (Слайд 11)
Решить задачу (задача распечатана на карточках).
Индусская задача
Из множества чистейших цветков лотоса третья была принесена в дар Шиве, пятая – Вишну, шестая часть – Солнцу. Одну четвёртую часть всех цветков получил Бхавани, а оставшиеся шесть цветков были даны высокочтимому учителю. Скажи, сколько было цветков лотоса?
Презентация прилагается.
Литература
-
Математика. 6 класс: учеб.для общеобразоват. учреждений / [Н.Я. Виленкин и др.]. – 21 – е изд., стер. – М.: Мнемозина, 2007. – 288с. : ил.
-
Перельман Я. И. Занимательная алгебра. – М.: ООО «ЮНИК инк», ИКТЦ «ЛАДА», 2006. – 192с.
-
Альхова З.Н., Макеева А. В. Внеклассная работа по математике. –
Саратов: «Лицей», 2001. – 288с. – (Библиотечка учителя).
-
Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4 – 8 кл сред. шк. - 5 – е изд. – М.: Просвещение, 1988. – 160с.: ил.
-
Выговская В.В. Поурочные разработки по математике: 6 класс. – М.: ВАКО, 2009. – 544с. – (В помощь школьному учителю).
Здесь представлен конспект к уроку на тему «Искусство составлять уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (6 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

