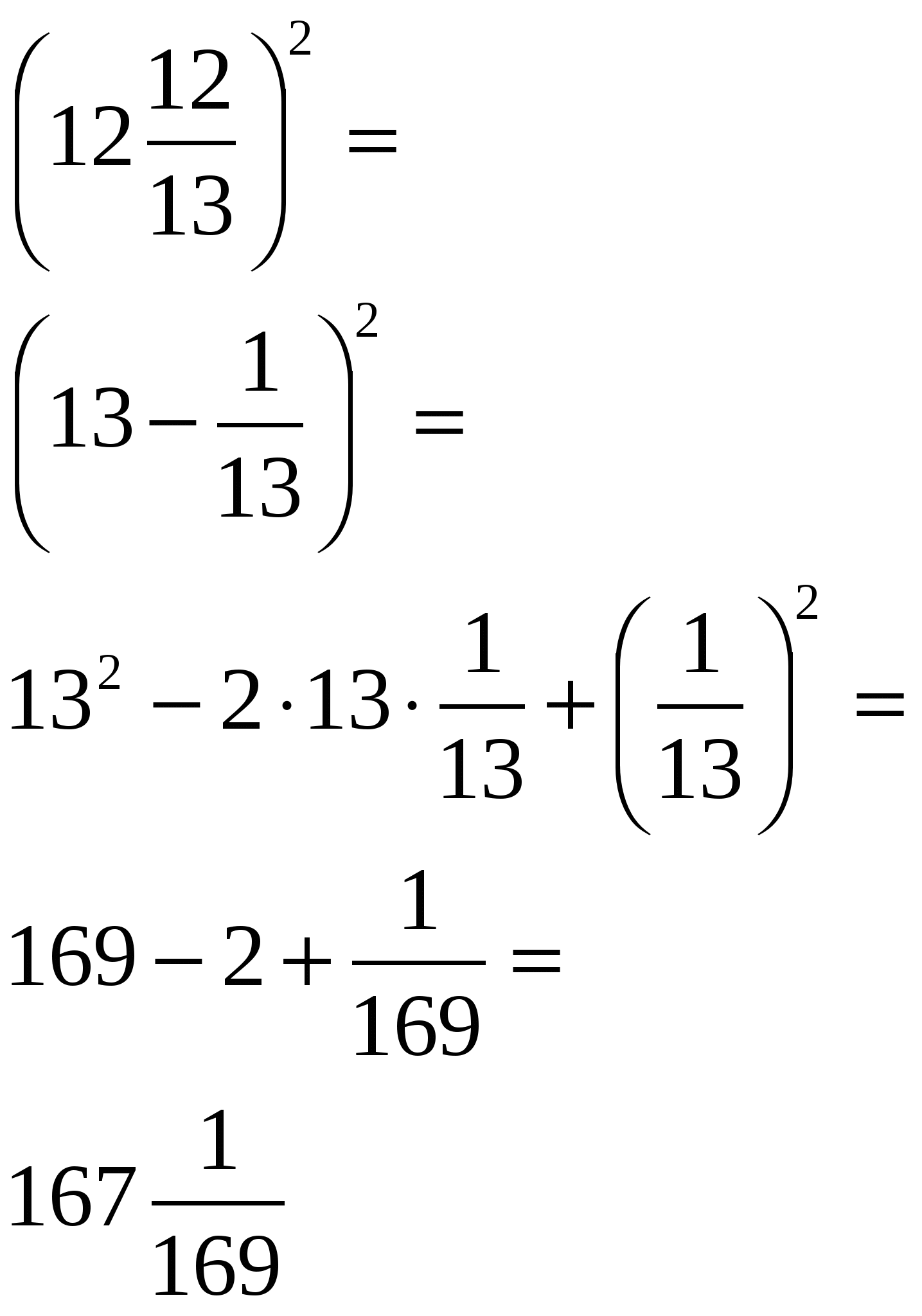Конспект урока «Формулы сокращенного умножения. Квадрат суммы и квадрат разности» по математике
Урок математики
Формулы сокращенного умножения.
Квадрат суммы и квадрат разности.
(конструирование урока
с использованием технологии УДЕ)
Составитель: Агринская Л.Ф.,
учитель МБОУ СОШ № 27 г.о. Самара
Не бойтесь формул! Учитесь владеть этим тонким инструментом человеческого гения! В формулах увековечены ценнейшие достижения людского рода, в них заключено величие и могущество разума, его торжество над покоренной природой.
Из книги “Машина“ под редакцией акад. И.И.Артоболевского
Дата проведения урока: 13.12.2013 г.
Тип урока: комбинированный
Цель урока: выработать у учащихся умение применять формулы (a±b)2= a2± 2ab+b2 как “слева направо”, так и “справа налево” в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.
Цели ученика: запомнить формулы (a±b)2= a2± 2ab+b2, уметь читать выражения, т.е. переходить от формул к их словесному выражению и наоборот, научиться применять эти формулы при выполнении упражнений, самостоятельно составлять задания.
Средства обучения: приемы технологии УДЕ, презентация Power Point
Оборудование урока: ноутбук, проектор, экран.
Местоположение урока в планировании
Всего на изучение темы: “Многочлены. Арифметические операции над многочленами” согласно тематическому планированию отводится 22 часа. Данный урок является в параграфе 17 первым, при изучении пункта учебника “Формулы сокращенного умножения”. К этому моменту учащиеся умеют умножать многочлен на одночлен, многочлен на многочлен.
Структура урока:
-
Организационный момент (2 мин).
-
Актуализация опорных знаний учащихся (5 мин).
-
Самостоятельная работа.
-
Проверка домашнего задания.
-
Изучение нового материала (5 мин).
-
Закрепление пройденного (12 мин).
-
Физкультминутка (1 мин).
-
Самостоятельная работа (10 мин).
-
Постановка домашнего задания (2 мин).
-
Подведение итогов (2 мин).
-
Рефлексия (1 мин).
Конспект урока алгебры в 7 классе
(учебник А.Г. Мордковича, методика П.М. Эрдниева)
-
Организационный момент.
-
Актуализация знаний учащихся.
1.Самостоятельная работа.
| Запишите | a и b | 0,5a и 2b | a и 2b2 | -ba и (-2b2) | |
| 1 | Квадрат одночлена | a2 и b2 | | | |
| 2 | Удвоенное произведение одночленов | 2ab | | | |
| 3 | Разность квадратов одночленов | a2- b2 | | | |
| 4 | Квадрат суммы одночленов | (a + b)2 | | | |
Проверку осуществляют консультанты (4чел.) по готовым ответам, сообщают результаты, какие ошибки были допущены.
2. Проверка домашнего задания.
№ 461-467(г) (устно)
В этих упражнениях нужно было выполнить умножение двучлена на себя, сравнить результат и исходное выражение, сделать вывод.
| (m-n)2= m2-2mn+n2 (12-p)2 = 144-24p+p2 (7y-6)2 = 49y2-84y+36 (-3m+4n)2= 9m2-24mn+16n2 |
-
Изучение нового материала.
Сделали вывод, что в некоторых случаях умножение многочленов можно выполнить короче, воспользовавшись формулами сокращенного умножения.
| (a-b)2= =(a-b)(a-b)= =(a-b)a-(a-b)b= =a2-ab-ab+b2= =a2-2ab+b2 |
Объединяя эти две формулы, мы можем записать совместно два тождества.
Тождеством называется равенство верное при любых значениях переменных.
| (a±b) (a±b)= a2±2ab+b2
Читая данные тождества справа налево, получаем формулы разложения многочлена на множители (2x+3)(2x+3)= 4x2+12x+9 (7y-6) (7y-6)= 49y2-84y+36 |
Квадрат ![]() двух чисел (a±b)2 равен трехчлену, состоящему из слагаемых:
двух чисел (a±b)2 равен трехчлену, состоящему из слагаемых:
1) квадрата первого числа (a2);
2) ![]() удвоенное произведение первого числа на второе (±2ab);
удвоенное произведение первого числа на второе (±2ab);
3) плюс квадрат второго числа (b2).
Геометрический смысл формулы
(a+b)2= a2+2ab+b2 для положительных чисел a и b
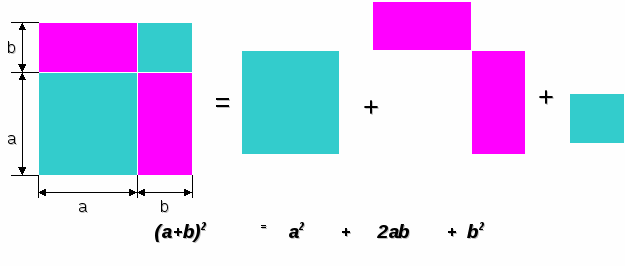
Геометрический смысл формулы (a-b)2= a2-2ab+b2 для положительных чисел a и b, удовлетворяющих условию a > b
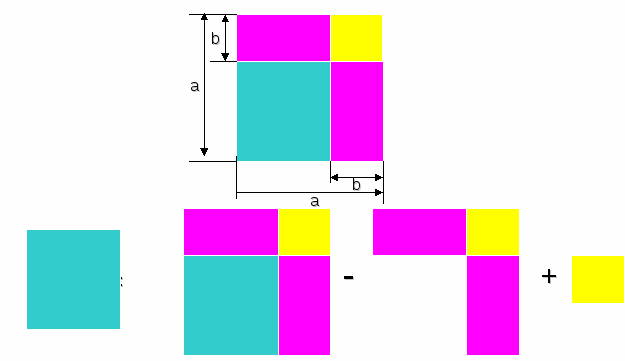
(a-b)2 = a2 - 2ab + b2
Схема
| x2 + + 9 6x
x 2 |
-
Закрепление
-
Формулы квадрата суммы и квадрата разности можно представить с помощью геометрических фигурок следующим образом:
(□ ± Δ)2 = □2 ± 2∙□∙Δ+ Δ2
Эти фигурки изображают “окошечки”, куда можно вписать различные одночлены, чтобы понять и запомнить эти формулы.
Заполните таблицу по образцу
| Δ | (□ + Δ)2 | □2 + 2∙□∙Δ+ Δ2 | Результат упрощения | |
| 2a | 6 | (2а+6)2= | (2a)2+2∙(2a)∙6+(6)2= | =4a2+24a+36 |
| 3а | -9 | (3а-9)2= | (3a)2+2∙(3a)∙(-9)+(-9)2= | =9a2-54a+81 |
| | | (3а+b)2= | | |
| | | (4а-b)2= | | |
| | | (а-5b)2= | | |
| | | (a2+2b3)2= | | |
| | | (3a-2b2)2= | | |
-
Восстановите пропущенные выражения
-
25-10b2+b4 =(▭-▭)∙(▭-▭)=(▭-▭)2
-
25±10b2+b4 =(▭±▭)2
б) ▭+14е +е2 = 72+2∙▭∙е +е2
(▭-▭)2= 49-▭+е2
(▭±▭)2 = 49±14е +е2
-
Выполните сокращение дробей, запишите пропущенные выражения; проверьте ответ умножением многочленов:
-
2
5+ 10а+а2 = ▭ = ▭
-
5+а
-
25- 10а+а2 = ▭ = ▭
5
-
Используя формулы (a±b)2, вычислите по аналогии
![]()
![]()
Образец:
а ) б)
) б)
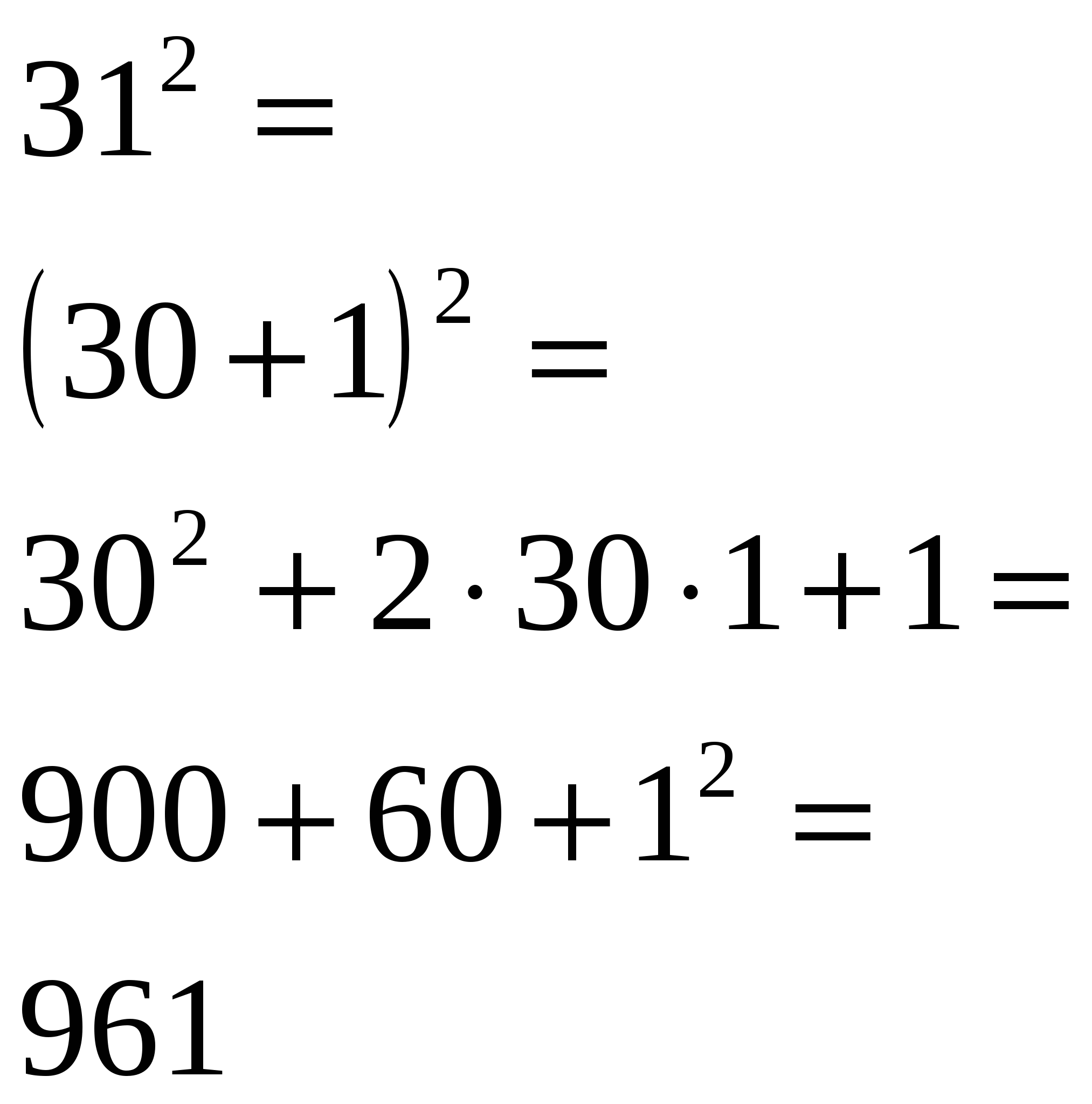
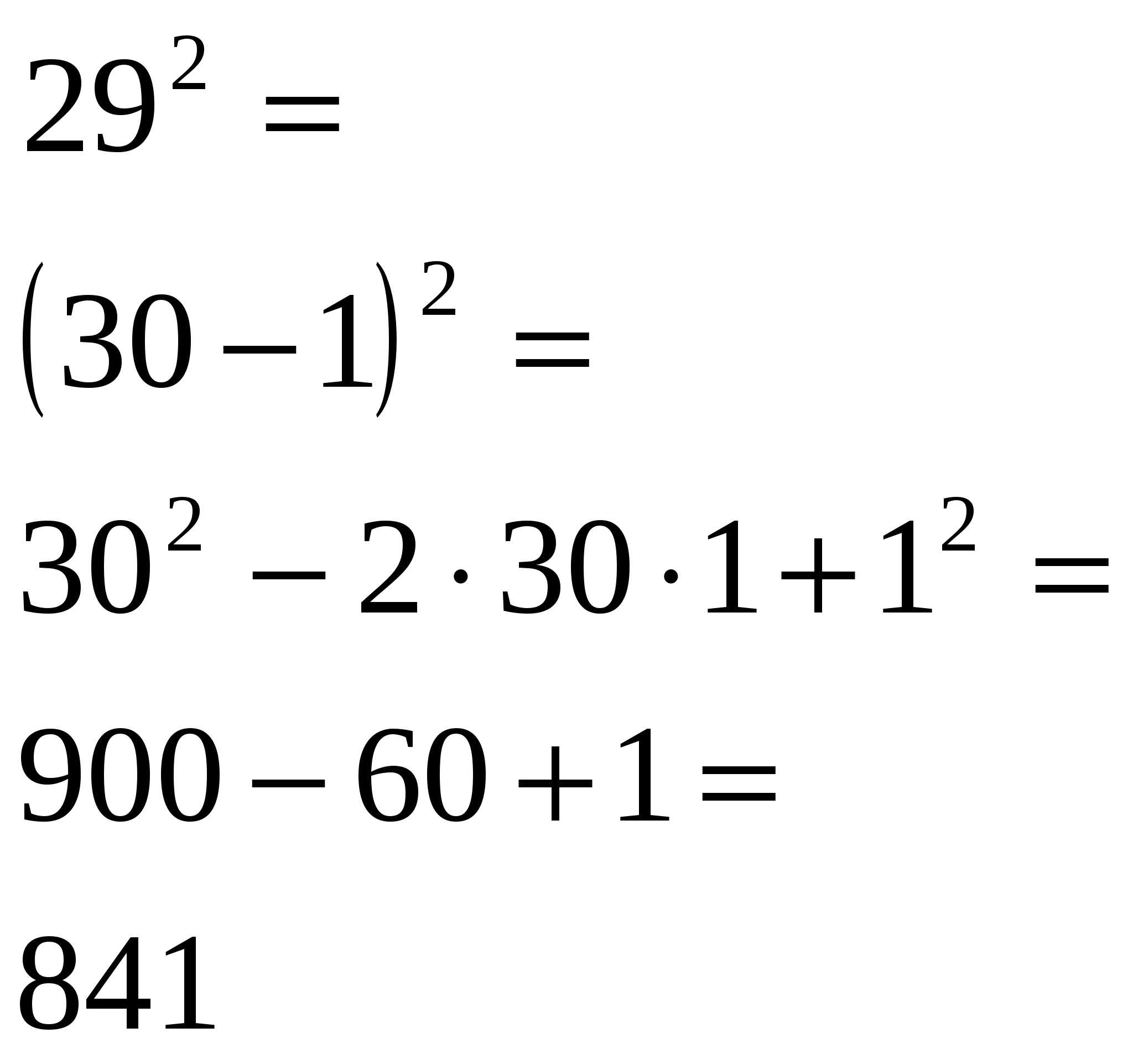
в ) г)
) г)
Ответы проверяются тут же на уроке. Если решение какого-либо примера не получилось у большинства учащихся, то его решение рассматривается на доске.
-
Самостоятельная работа (тетради взять на проверку).
Вариант 1:
1. Преобразуйте выражения:
а) (2x-5)2;
б) (3а + b2)2
2. Докажите, что (-а-b)2=(а+b)2
3. Дополните до квадрата суммы и квадрата разности:
а) а2+2аb+ ▭=(а+b)2
б) n2-4mn+ ▭=(▭-▭)2
в) 4а6- ▭+ b2=(▭-▭)2
-
Не выполняя вычислений, сравните значения выражений (28+72)2 и 282+722
-
Вычислите, используя формулы сокращенного умножения:
а) 422
б) 1412-2∙141∙41+412
Вариант 2:
1. Преобразуйте выражения:
а) (5x-2)2;
б) (4а + b2)2
2. Докажите, что (x-2)2=(2-x)2
3. Дополните до квадрата суммы и квадрата разности:
а) а2-2аb+ ▭=(а-b)2
б) m2+6mn+ ▭=(▭+▭)2
в) 9а8+▭+ b4=(▭+▭)2
-
Не выполняя вычислений, сравните значения выражений (35+65)2 и 352+652
-
Вычислите, используя формулы сокращенного умножения:
а) 312
б) 552+2∙55∙25+252
-
Итог урока.
-
Домашнее задание.
п.17 (геометрическое доказательство формул),
№ 474-477(г) (выполнить классификацию примеров по принципу + и -),
№ 457.
Здесь представлен конспект к уроку на тему «Формулы сокращенного умножения. Квадрат суммы и квадрат разности», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

 итая эти тождества слева направо, получаем формулы сокращенного умножения
итая эти тождества слева направо, получаем формулы сокращенного умножения


 ∙3∙x
∙3∙x