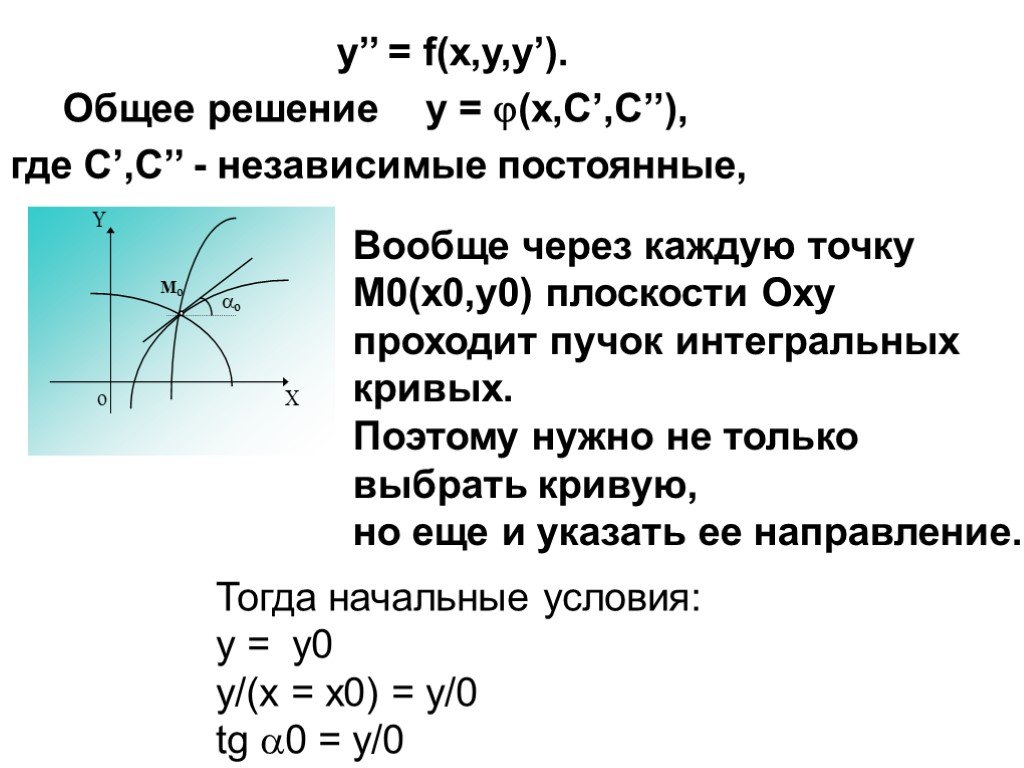
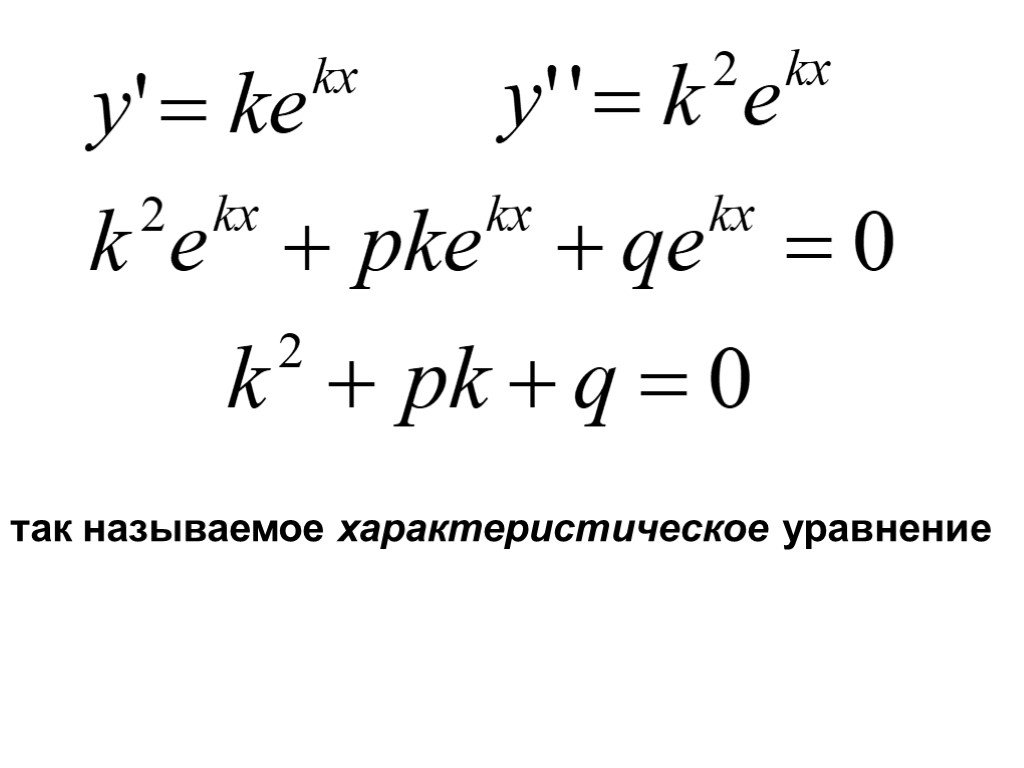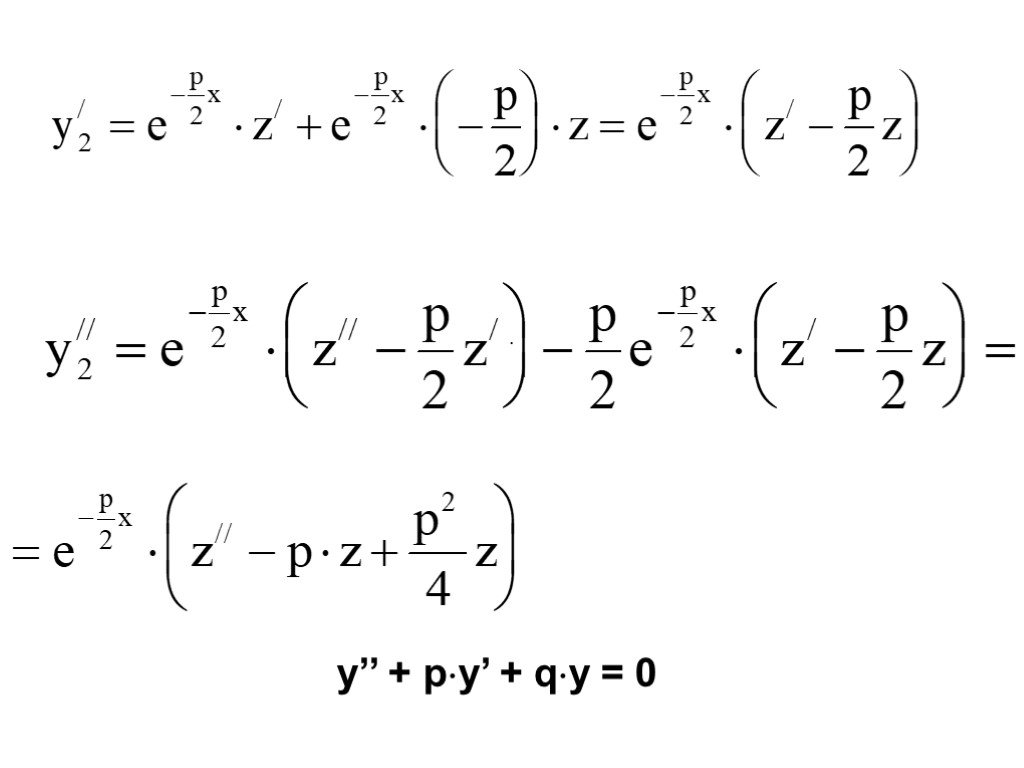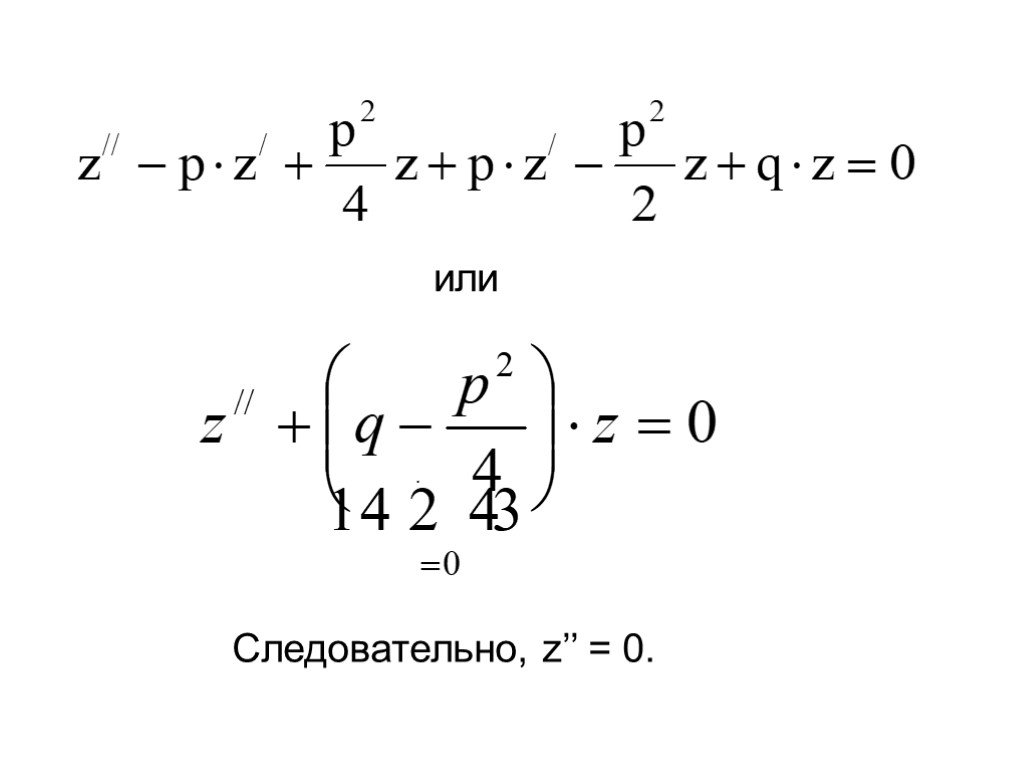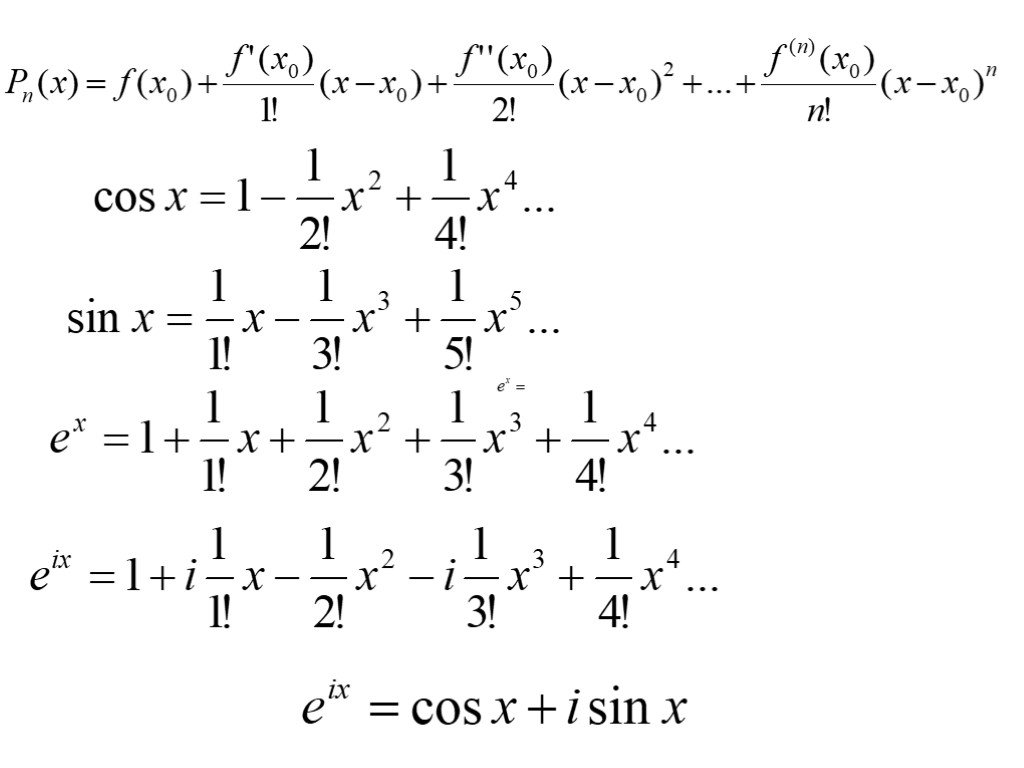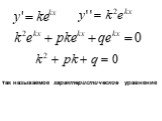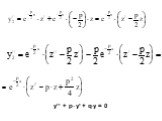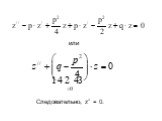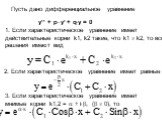Презентация "Дифференциальные уравнения второго порядка" по математике – проект, доклад

Уроки 8-9

Дифференциальные уравнения второго порядка

y’’ = f(x,y,y’). y = (x,C’,C’’), Общее решение

где С’,С’’ - независимые постоянные,

Тогда начальные условия: у = у0 y/(х = х0) = y/0 tg 0 = y/0

Вообще через каждую точку М0(х0,у0) плоскости Оху проходит пучок интегральных кривых. Поэтому нужно не только выбрать кривую, но еще и указать ее направление.

Пусть имеем линейное дифференциальное однородное уравнение y’’ + py’ + qy = 0. (2.8) где p, q - постоянные коэффициенты. Будем искать частное решение в форме

Линейные однородные уравнения второго порядка с постоянными коэффициентами

k = Const и ее нужно определить.

так называемое характеристическое уравнение

Для составления характеристического уравнения достаточно в уравнении производные у’’, у’ и саму функцию у заменить на соответствующие степени k.

, : ; 1.

следовательно, имеем два действительных корня k1 и k2. Следовательно, уравнение допускает два различных частных решения

если k1k2, то эти решения будут линейно независимы.

Определение. Два решения у1 и у2 называются линейно зависимыми, если можно подобрать постоянные числа а1 и а2, неравные одновременно нулю, такие, что линейная комбинация этих функций тождественно равна нулю, то есть а1у1 + а2у2  0. В противном случае (то есть если таких чисел подобрать нельзя) у1 и у2 называются линейно независимыми. Тогда общее решение данного уравнения есть линейная комбинация этих частных решений

. : . . 2. , следовательно,

В этом случае корень называется кратным, и частное решение будет одно

Всякое другое частное решение у2, линейно независимое с у1, обязательно должно иметь вид у2 = у1z(x),

где z(x) - некоторая функция, не являющаяся константой

y’’ + py’ + qy = 0

или

Следовательно, z’’ = 0.

Тогда z’ = a и z = ax + b, где a и b - произвольные константы. И, следовательно,

Если нам нужно только частное решение, то можно принять а=1,b=0 и тогда

То есть общее решение уравнения во втором случае имеет вид

. 3.

3.

, то будем иметь два сопряженных комплексных корня

и

k1 =  + i и k2 =  - i, где

Таким образом, общее решение имеет вид

Пусть дано дифференциальное уравнение

1. Если характеристическое уравнение имеет действительные корни k1, k2 такие, что k1  k2, то все решения имеют вид

2. Если характеристическое уравнение имеет равные действительные корни k=k1=k2, то решение имеет вид

3. Если характеристическое уравнение имеет мнимые корни k1,2 =   i, (  0), то