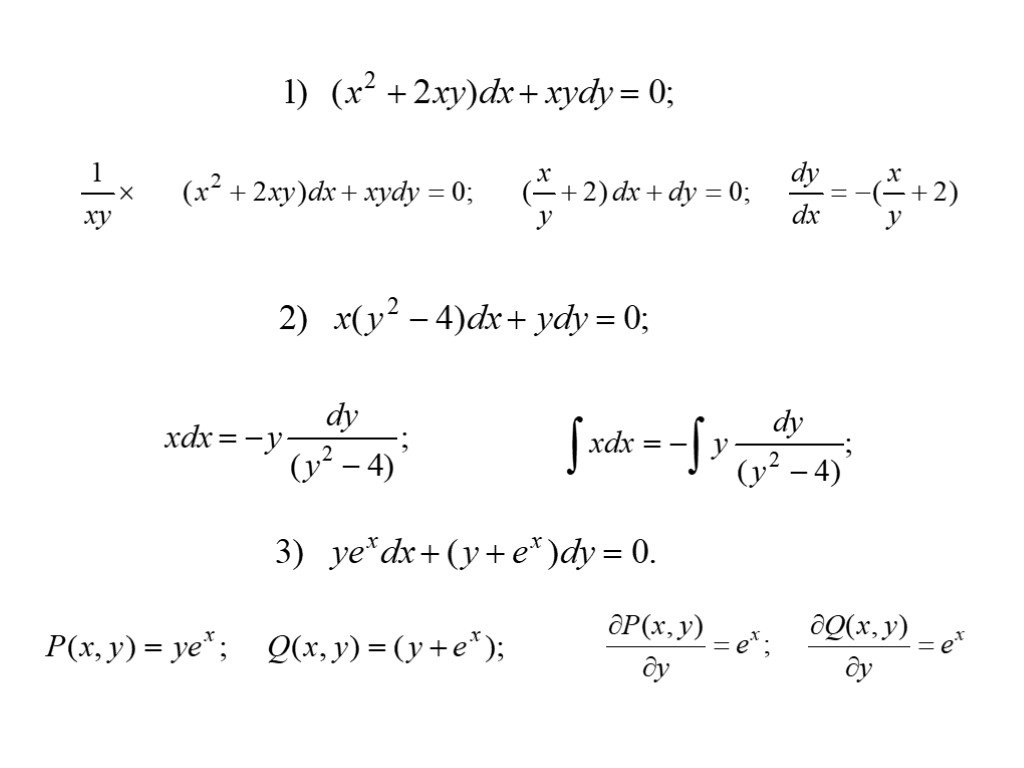Презентация "Обыкновенные дифференциальные уравнения" по математике – проект, доклад
Презентацию на тему "Обыкновенные дифференциальные уравнения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 26 слайд(ов).
Слайды презентации
Список похожих презентаций
Обыкновенные дифференциальные уравнения
Уравнение первого порядка. Функциональное уравнение F(x,y,y) = 0 или y= f(x,y), связывающее между собой независимую переменную, искомую функцию ...линейные дифференциальные уравнения первого порядка
Опрос. 1. Какое уравнение называется дифференциальным? Уравнение, содержащее производные искомой функции или её дифференциалы. 3.Что значит решить ...Дифференциальные уравнения высших порядков
1. Общие сведения. Определение. Дифференциальное уравнение содержащее производную функции двух и более порядков, называется дифференциальным уравнением ...Дифференциальные уравнения первого порядка
Презентация На тему:. «Дифференциальные уравнения. первого порядка». Подготовил студент группы К-11 Свиноренко Станислав. План:. Простейшие дифференциальные ...Дифференциальные уравнения второго порядка
y’’ = f(x,y,y’). y = (x,C’,C’’), Общее решение. где С’,С’’ - независимые постоянные,. Тогда начальные условия: у = у0 y/(х = х0) = y/0 tg 0 = y/0. ...Математическая игра. Обыкновенные дроби
Правила игры. Выбор первого игрока. Отгадайте ребус Правильный ответ Линейка ЧИ Число. За два дня отремонтировано км дороги. За первый день отремонтировано ...Тригонометрические уравнения
Верно ли, что:. Имеют ли смысл выражения:. Решить уравнение:. Пример 1. Решить уравнение 2 sin2x + sinx - 1 = 0. Решение. Введём новую переменную ...Решение квадратного уравнения
Формула корней квадратного уравнения. Устный счёт. 1.Определить по какому признаку написаны уравнения и какое из них лишнее и почему? Решить устно ...Простейшие показательные уравнения
Цели урока.Выявить общий вид показательного уравнения Выяснить способы его решения Научиться решать простейшие показательные уравнения. Решите уравнения ...
Вывод канонического уравнения эллипса
Цели и задачи. Цели: Рассмотреть основные понятия по теме «Вывод канонического уравнения эллипса» Задачи: Рассмотреть свойства эллипса Исследовать ...Обыкновенные дроби и смешанные числа. Устный счет
? ? + ? ? ? ? =. ? ?? + ? ?? ?? ?? ? ?? + ? ?? ?? ?? ? ?? + ? ?? ?? ?? ?? ?? − ? ?? ? ?? ?? ?? − ? ?? ? ?? ?? ?? − ? ?? ?? ?? ?? ?? − ? ?? ? ?? ?? ...Обыкновенные дроби
План урока. Повторение Основное свойство дроби Сокращение дробей. Повторение. Вспомни: Обыкновенная дробь. a-числитель, b- знаменатель. Правильная ...Диофантовы уравнения
Цели и задачи. Определение диофантова уравнения Биография Диофанта Диофантовые уравнения первой степени Диофантовые уравнения высших степеней Проект ...Диофантовы уравнения
СКОЛЬКО РЕШЕНИЙ ИМЕЕТ ДАННОЕ УРАВНЕНИЕ? (2х+у)(5х+3у)=7. 3) Не имеет решений. 4) Бесконечно много решений. Следующее задание. (3х+7у)(х-у)=13 1) 2 ...Диофантовы уравнения
Диофантовы уравнения Глобально не изучаются в школьной программе, а присутствуют на экзамене! Проблема подтолкнувшая на создание работы:. обусловлена ...Диофантовы уравнения
Цели учебно – исследовательской работы: изучить способы решения диофантовых уравнений; повысить уровень математической культуры, прививая навыки самостоятельной ...Графическое решение линейного уравнения с двумя переменными
Цель урока:. проверить прочность знаний, умений и навыков, учащихся по данной теме, обеспечить закрепление и обобщение изученного материала; развивать ...Графики линейного уравнения с двумя переменными
Цель урока:. ввести понятие графика уравнения с двумя переменными; повторить построение графика линейной функции по двум точкам; закрепить навыки ...График линейного уравнения с двумя переменными
Закончите предложение:. Линейным уравнением с двумя переменными называется уравнение вида. ах+by=с, где х и y – переменные, а, b и с – некоторые числа. ...Неполные квадратные уравнения
Математику нельзя изучать, наблюдая, как это делает сосед! А. Нивен. 1. Какое уравнение называется квадратным? 2. Может ли коэффициент а в квадратном ...Конспекты
Решаем уравнения с увеличением
Класс: 1. . Тема: Решаем уравнения с увеличением. . . Цель:. развивать вычислительные навыки. Знать. геометрические фигуры, ряд натуральных ...Составные уравнения
Математика. УМК: образовательная система «Школа 2100». 3 класс. Дергунова Татьяна Ивановна. учитель начальных классов. МБОУ «Ардатовская основная ...Повторение: логарифмы, логарифмические уравнения
Преподаватель: Гаученова Валентина Петровна. Забайкальский край. Государственное профессиональное образовательное учреждение «Чернышевское многопрофильное ...Показательные функции, уравнения, неравенства
Обобщающий урок. по теме:. Учитель математики филиала. . БОУ ХМАО - Югры В(с)ОШ. при ИР 99/15 г.Нижневатовска. ...Обыкновенные дроби
Тема урока:. «Обыкновенные дроби». Цель урока:. закрепить пройденный материал по теме: «Обыкновенные дроби»; развить практические навыки путем ...Обыкновенные дроби. Правильные и неправильные дроби
Методическая разработка урока проверки знаний. Урок математики в 5-м классе. Повторение по теме "Обыкновенные дроби. Правильные и неправильные дроби". ...Доли. Обыкновенные дроби
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа №18 с УИОП. Орехово-Зуевского района Московской области. ...Обыкновенные дроби
Конспект открытого урока по математике. . в 5 классе по теме «Обыкновенные дроби». /урока актуализации знаний и умений (урок повторения)/. ...Доли. Обыкновенные дроби
Конспект урока математики на тему «. Доли. Обыкновенные дроби». Цели:. Образовательные:. . . учить читать, записывать и понимать обыкновенные ...Доли. Обыкновенные дроби
Урок изучение нового материала по теме. . «Доли. Обыкновенные дроби» в 5 классе. Кленикова Ольга Николаевна. Учитель математики. . МБОУ ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 июня 2019
Категория:Математика
Содержит:26 слайд(ов)
Поделись с друзьями:
Скачать презентацию