Презентация "Дробно-рациональные уравнения" по математике – проект, доклад
Презентацию на тему "Дробно-рациональные уравнения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
Дробно-рациональные уравнения
Тема урока: Дробно-рациональные уравнения. Предметные знания и умения. Обогатить методологический аппарат правомерностью использования нового алгоритма ...Алгебраические уравнения произвольных степеней
Алгебраические уравнения произвольных степеней. 1. Введение. Всякий школьник, прежде всего, умеет решать уравнение первой степени: если дано уравнение ...Формула корней квадратного уравнения
Вы хотите научиться решать квадратные уравнения? ДА НЕТ. . . Содержание. Определение квадратного уравнения Дискриминант квадратного уравнения Формула ...Тригонометрические уравнения
Тригонометрические уравнения. Уравнение представляет собой наиболее серьёзную и важную вещь в математике. О.Лодж. «Дороги не те знания, которые откладываются ...Решение уравнений в целых числах. Диофантовы уравнения
Диофантовы уравнения. Алгебраические уравнения с целыми коэффициентами, решаемые во множестве целых чисел, вошли в историю математики как диофантовы. ...Простейшие тригонометрические уравнения
История развития тригонометрии. . . . . . . . . . . Устная работа. Ответьте на вопросы:. Может ли косинус быть равным: 0,75; 5/3; -0,35; π/3; 3/π; ...Показательные уравнения и способы их решения
Определение: Показательные уравнения – уравнения, в которых переменная входит только в показатели степеней при постоянных основаниях. Например,. Основные ...Показательные уравнения
Показательные. Цели урока: 1. ввести понятие показательных уравнений; 2. формировать умение решать показательные уравнения основными методами: функционально-графическим, ...Диофантовы уравнения
Цели учебно – исследовательской работы: изучить способы решения диофантовых уравнений; повысить уровень математической культуры, прививая навыки самостоятельной ...Графическое решение линейного уравнения с двумя переменными
Цель урока:. проверить прочность знаний, умений и навыков, учащихся по данной теме, обеспечить закрепление и обобщение изученного материала; развивать ...Графики линейного уравнения с двумя переменными
Цель урока:. ввести понятие графика уравнения с двумя переменными; повторить построение графика линейной функции по двум точкам; закрепить навыки ...График линейного уравнения с двумя переменными
Закончите предложение:. Линейным уравнением с двумя переменными называется уравнение вида. ах+by=с, где х и y – переменные, а, b и с – некоторые числа. ...Вывод канонического уравнения эллипса
Цели и задачи. Цели: Рассмотреть основные понятия по теме «Вывод канонического уравнения эллипса» Задачи: Рассмотреть свойства эллипса Исследовать ...Арксинус. Решение уравнения sin t = a
Цели. Изучить определение арксинуса числа. Изучить формулы решения простейшего тригонометрического уравнения sin t = a. Повторим. Что называется синусом ...Арккосинус и решение уравнения cos x = a
Цели урока. ввести понятие arccos x; вывести формулу решения уравнения cos x=a, ; рассмотреть уравнения на применение этой формулы; рассмотреть простейшие ...Обыкновенные дифференциальные уравнения
Уравнение первого порядка. Функциональное уравнение F(x,y,y) = 0 или y= f(x,y), связывающее между собой независимую переменную, искомую функцию ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0. 1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...Диофантовы уравнения
Диофантовы уравнения Глобально не изучаются в школьной программе, а присутствуют на экзамене! Проблема подтолкнувшая на создание работы:. обусловлена ...Показательные уравнения
Математический диктант. Запишите функции. 1. Постройте схематично графики. 2. Выпишите убывающие функции 3. Для каждой из функций запишите множество ...Диофантовы уравнения
СКОЛЬКО РЕШЕНИЙ ИМЕЕТ ДАННОЕ УРАВНЕНИЕ? (2х+у)(5х+3у)=7. 3) Не имеет решений. 4) Бесконечно много решений. Следующее задание. (3х+7у)(х-у)=13 1) 2 ...Конспекты
Дробно-рациональные уравнения
РЕШЕНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ. Цели урока:. Обучающая:. формирование понятия дробно- рационального уравнения;. . рассмотреть различные ...Неравенства и уравнения, содержащие степень
Неравенства и уравнения, содержащие степень. Цель:. провести систематизацию и обобщение знаний по вопросам решения уравнений и неравенств; рассмотреть ...Целые уравнения
Открытое занятие элективного курса. . по алгебре в 9 классе. ( Продолжительность 1 ч 30 мин). Разработала. учитель математики МАОУ СОШ №10. ...Формула корней квадратного уравнения
Урок по теме. . «Формула корней квадратного уравнения. ». Организационная информация. Тема урока:. . «Формула корней квадратного уравнения. ...Тригонометрические уравнения
Захарова Людмила ВладимировнаМБОУ «Средняя общеобразовательная школа № 59» г. Барнаулаучитель математики. zlv-13@mail.ru. ...Системы линейных уравнения с двумя переменными
Учитель математики ГБОУ СОШ № 80. . с углубленным изучением английского языка. . Головкина. Светлана Анатольевна. Разработка урока по алгебре ...Рациональные уравнения как математические модели реальных ситуаций
ПЛАН-КОНСПЕКТ УРОКА Рациональные уравнения как математические модели реальных ситуаций. . ФИО (полностью). . Науменкова Олеся Анатольевна. ...Показательные уравнения и неравенства
Технологическая карта урока по математике в 10 классе. по теме: «Показательные уравнения и неравенства». Учитель Бондарь Ирина Рувиновна. Предмет. ...Дробные рациональные уравнения
Урок по алгебре в 9 классе. Тема урока:. Дробные рациональные уравнения. Цели урока:. 1) Организовать деятельность учащихся, способствующую формированию ...Дробные рациональные уравнения
Тема урока:. «Дробные рациональные уравнения». Класс 9. Тип урока:. комбинированный. Цели: 1. . Образовательные:. Дать определение «дробно-рациональные ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:18 октября 2018
Категория:Математика
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию














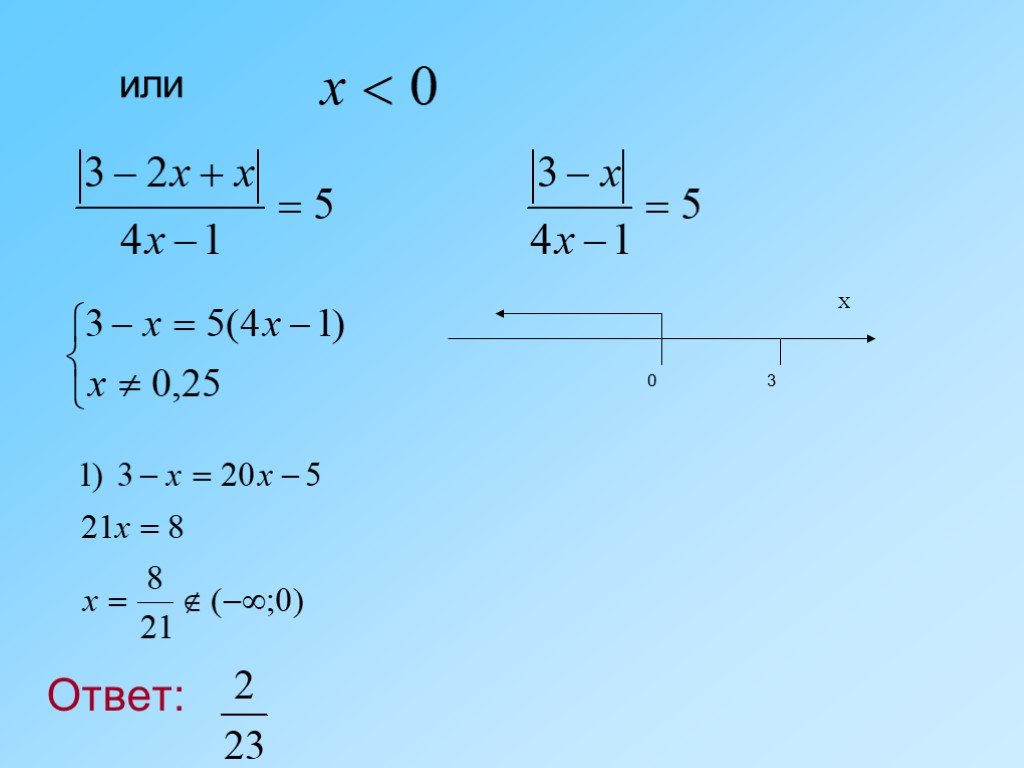




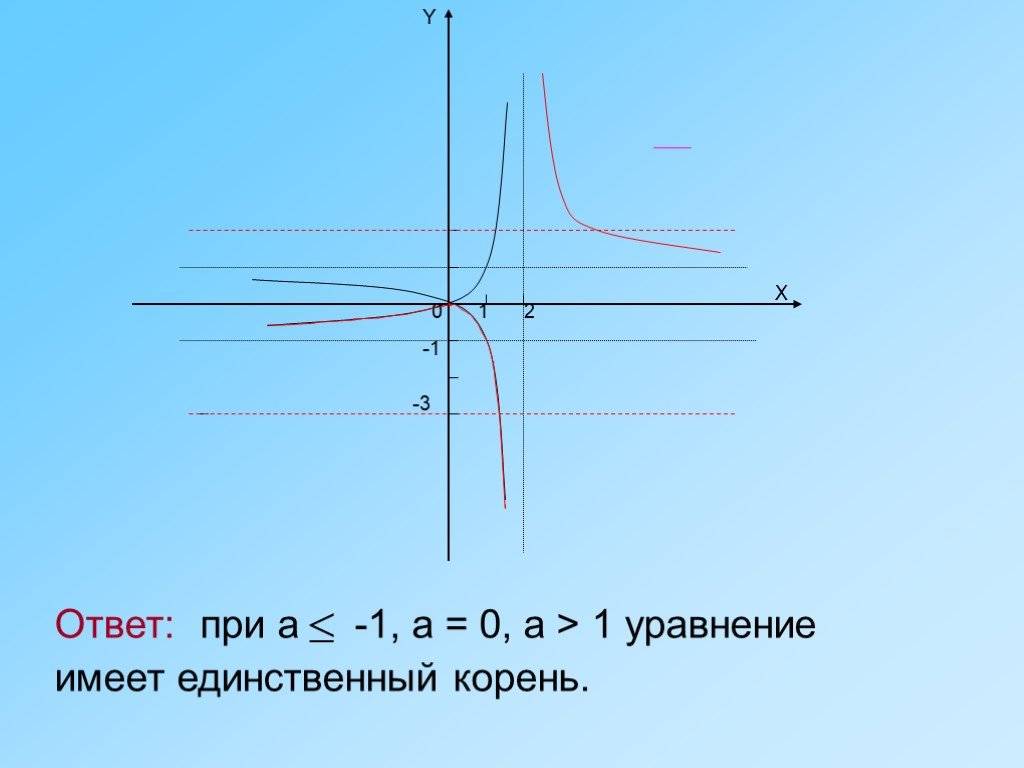









![2 способ: метод разбиения на промежутки. Нанесем на числовую прямую значение х, при котором х-5=0 и значение х, при котором х+2=0. Числовая прямая при этом разобьется на промежутки: ( -∞; -2 ), ( -2; 5 ], [ 5; + ∞ ). Решим заданное уравнение на каждом из этих промежутков. 2 способ: метод разбиения на промежутки. Нанесем на числовую прямую значение х, при котором х-5=0 и значение х, при котором х+2=0. Числовая прямая при этом разобьется на промежутки: ( -∞; -2 ), ( -2; 5 ], [ 5; + ∞ ). Решим заданное уравнение на каждом из этих промежутков.](https://prezentacii.org/upload/cloud/18/10/89185/images/thumbs/screen10.jpg)