Конспект урока «Формула корней квадратного уравнения» по алгебре для 8 класса




Формула корней квадратного уравнения
Алгебра, 8 класс
Автор: Критинина О.М. – учитель математики МКОУ БООШ №5
Бутурлиновского района
Воронежской области.
«Ум заключается не только в знании,
но и умении прилагать знания на деле»
Аристотель
Цель:
знакомство с формулами корней квадратного уравнения.
Задачи урока:
-
Образовательные: ввести понятие квадратного уравнения, раскрыть содержание понятия квадратное уравнение, познакомить учащихся с основными формулами нахождения корней квадратного уравнения.
-
Развивающие: формировать умения находить корни квадратного уравнения, используя его определение и формулы; развивать вычислительные навыки, умения анализировать и обобщать; развивать интерес к математике.
-
Воспитательные: воспитывать активность, культуру эмоций, точность, аккуратность.
Универсальные учебные действия (УУД):
-
Личностные УУД
-
Регулятивные УУД
-
Коммуникативные УУД
-
Познавательные УУД
Планируемые результаты:
Предметные:
-
знать определение квадратного уравнения, формулы корней квадратного уравнения;
-
уметь решать квадратные уравнения
Личностные: активность на уроке, аккуратность ведения записей в тетради обучающихся.
Метапредметные:
-
активное использование речевых средств и средств информационных и коммуникационных технологий для решения коммуникативных и познавательных задач;
-
использование различных способов поиска (в справочных источниках и открытом учебном информационном пространстве сети Интернет), сбора, обработки, анализа, организации, передачи и интерпретации информации в соответствии с коммуникативными и познавательными задачами и технологиями учебного предмета.
Основные понятия: формула корней квадратного уравнения, дискриминант, коэффициенты.
Ресурсы:
-
Основные: тетрадь, учебник
-
Дополнительные: таблица «Лист проблем», тест «Верю, не верю», презентация, ПК, проектор, экран.
Формы урока: фронтальная, индивидуальная.
Ход урока:
Стадия вызова.
Здравствуйте, садитесь.
«Сегодня у нас будет необычный урок. Я не буду, как обычно, сообщать вам тему урока. Вы сами в течение урока попробуете ее сформулировать и определить цели и задачи нашего урока. В помощь Вам я прочитаю небольшую лекцию.
Текст лекции.
«Мы с Вами с начальной школы решаем уравнения. В 6 классе Вы уже знали, как решать линейные уравнения, например 2х+5=3х ,которое имеет один корень, в 8 классе изучали уравнения х2=а,которое имеет два корня противоположных знаков:2 и -2; 3 и -3. Но если бы Вам предложили уравнение х2+5х+3=5, то Вы лишь бы предположили, что оно имеет 2 корня противоположных знаков. Но записать их не смогли.
Работая в паре, предлагаю Вам заполнить 1-4 пункты таблицы, которая лежит на Ваших столах (учащиеся знакомятся с таблицей). Время на выполнение работы – 3 мин.
Чтобы вам было легче заполнить таблицу, я повторю ещё раз свою лекцию (учитель читает второй раз ту же лекцию, но в более быстром темпе).
| |||
| | | ||
| 3. Какие вопросы, связанные с проблемой Вас интересуют? | 4. Что Вы об этом знаете или предполагаете, что знаете? | 5. Что об этом Вы узнали? | 6.Ваши ассоциации |
| | | | |
Обсуждение. В ходе обсуждения учитель будет с учащимися заполнять аналогичную таблицу на доске, поэтому её необходимо приготовить заранее (до урока).
- И так, кто догадался, какую проблему мы сегодня хотим решить? (Обычно находится ученик, который смог догадаться, что это решение квадратного уравнения. )
- Может бытьуже можно сформулировать и тему нашего урока? (Учащиеся формулируют тему урока).
- Какой информацией вы обладаете для решения этой проблемы?
- Какие вопросы, связанные с проблемой Вас интересуют?
Первоначально вопросы по теме, которые назовут учащиеся, лучше записать за пределами таблицы. Затем вместе с учащимися их систематизировать и записать коротко в столбец 3 таблицы. Примеры ответов учеников: форма записи корней уравнения, существование корней, при каких условиях уравнение имеет решение, введение нового символа для нахождения корней, название этого символа. И последнее, что осталось обсудить - что ученики об этом знают или предполагают, что знают.
Стадия осмысления.
Учитель продолжает.
Теперь возникает вопрос – правы ли мы были в своих предположениях?
-Какова же тема нашего урока? Совпала ли она с той, что Вы предположили ранее? И каковы цели нашего урока? Откройте тетради и запишем в ней тему нашего урока: « Формула корней квадратного уравнения».
Цели урока учитель формулирует (со слов учащихся) устно: усвоить понятие дискриминанта, научиться находить корни квадратного уравнения.
Конечно же, до нас уже эту проблему уже решали, поэтому я предлагаю Вам обратиться к презентации.
(слайд 3)
Определение. Квадратным уравнением называется уравнение вида ах2+bх+с=0, где х – переменная, а,b,с – некоторые числа, причем а≠0.
Квадратное уравнение , в котором коэффициент при х2 равен 1, называют приведенным квадратным уравнением. Например, х2-11х+30=0, х2-6х=0, х2-8=0.
Если в квадратном уравнении ах2+вх+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называют неполным квадратным уравнением.
Как решать неполные квадратные уравнения и выделением квадрата двучлена мы с вами научились.
А сегодня научимся решать квадратные уравнения с помощью формул.
Итак, рассмотрим квадратное уравнение ах2+bх+с=0.

Дискриминантом квадратного
уравнения ах2+ bх + с = 0
называется выражение b2 – 4ac.
Его обозначают буквой D, т.е.D= b2 – 4ac.
Возможны три случая:
D> 0
D= 0
D 0
1.Если D> 0
В этом случае уравнение ах2+ bх + с = 0 имеет два действительных корня:
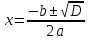
2.Если D=0
В этом случае уравнение ах2+ bх + с = 0 имеет один действительный корень:
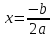
3.Если D
Уравнение ах2+ bх + с = 0 не имеет действительных корней.
Правило для решения квадратного уравнения:
-
Вычислить дискриминант и сравнить его с нулем;
-
Если дискриминант положителен или равен нулю , то воспользоваться формулой корней, если дискриминант отрицателен, то записать , что корней нет.
Формирование умений и навыков.
Решение примеров из учебника №534 (а, в), №535 (б,д), №537 (а,б)
Стадия рефлексии.
1. Тест «Верю, не верю».
| Верю, не верю (+, -) | |
| 1.В квадратном уравнении 5х2+2х+3=0 коэффициент при первом множителе равен 5. 2. В квадратном уравнении 6х2+4х-2=0, с=2 2. В квадратном уравнении 5х2+2х+0,b=2. 3.Если D>0, то уравнение имеет 2 корня. 4.Если D0, то уравнение не имеет корней. 5.Если D=0, то уравнение имеет 1 корень. 6.В квадратном уравнении 2х2+3х+1=0 D=1 7.В квадратном уравнении х2+5х+6=0 D=1 8.В квадратном уравнении 2х2+х+2=0 D=5 | |
3.Проанализируем таблицу и с учетом полученных знаний ответим на вопрос, что же мы узнали сегодня на уроке. Работают ученики в таблице, учитель на доске заполняют 5,6 пункт таблицы.
4.Итог урока, оценки учащихся
Здесь представлен конспект к уроку на тему «Формула корней квадратного уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

