Конспект урока «Арифметический способ отбора корней в тригонометрических уравнениях» по алгебре для 11 класса
Конспект урока для 11 класса на тему «Арифметический способ отбора корней в тригонометрических уравнениях»
Цели и задачи урока:
-
повторение по теме «Решение тригонометрических уравнений»; закрепление основных понятий базового уровня, умений и навыков по применению арифметического способа отбора корней в тригонометрических уравнениях.
-
развитие познавательного интереса, логического мышления, интеллектуальных способностей; формирование математической речи;
-
воспитание самостоятельности мышления у учащихся.
Тип урока: урок повторения.
Формы работы: индивидуальная, фронтальная, коллективная
Оборудование: компьютер, мультимедийный проектор, экран, презентация «Арифметический способ отбора корней в тригонометрических уравнениях».
Ход урока:
-
Организационный момент. (Сообщение темы, целей и задач урока)
-
Устная работа.
-
Расположите в порядке убывания числа:
![]()
-
Расставьте в порядке возрастания числа:
![]()
-
Сравните числа:
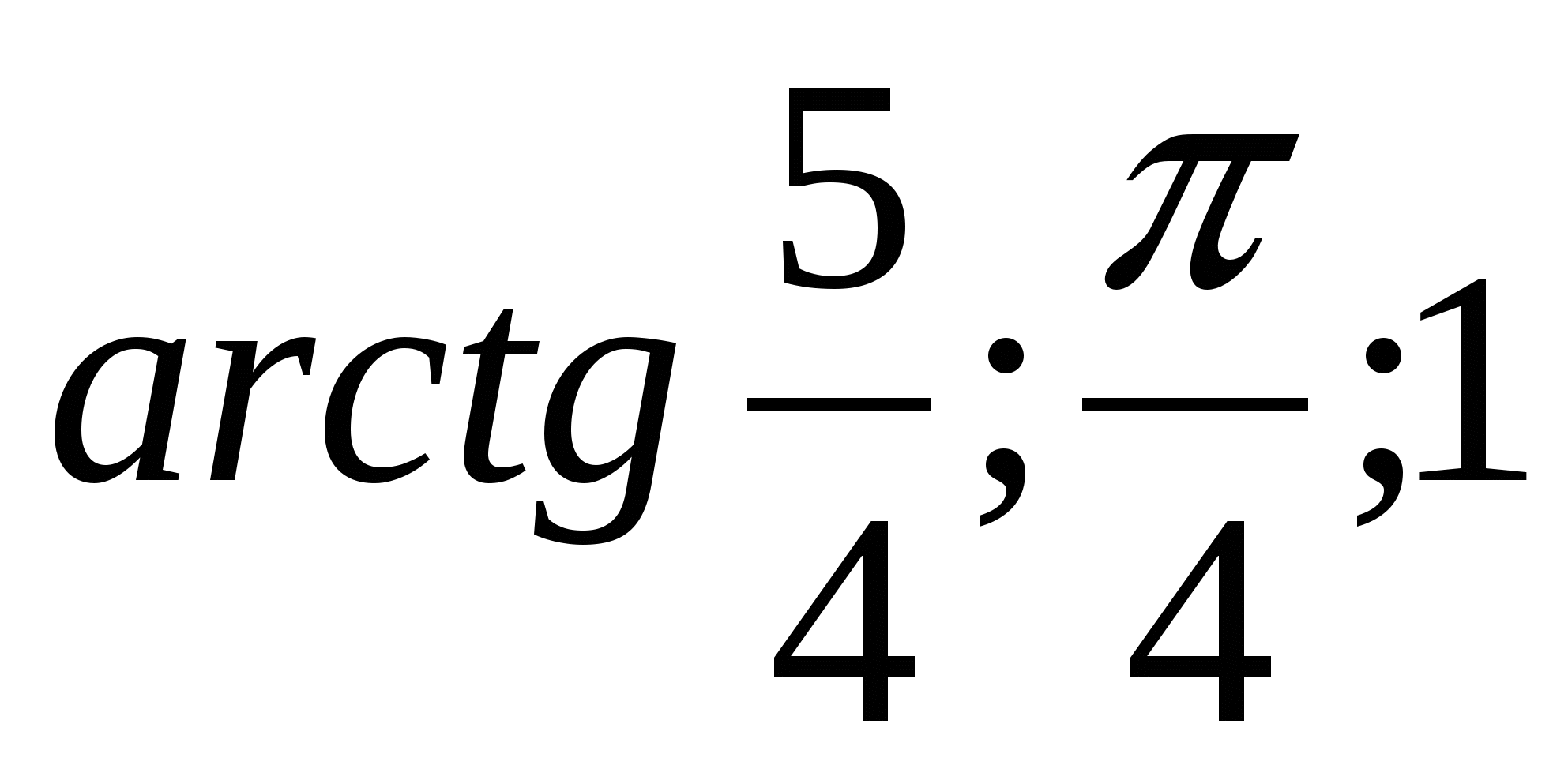
-
Вычислите:
(В результате выполнения задания мы повторим определения арккосинуса, арксинуса, арктангенса и арккотангенса)
а) arcsin1; б) arccos![]() ; в) arcsin (- 2); г) arctg
; в) arcsin (- 2); г) arctg ![]() ;
;
д) arccos![]() ; е) arсctg
; е) arсctg![]()
-
Повторение.
-
Формулы решения простейших тригонометрических уравнений
| Общая формула серии уравнений | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Следует отметить внимание учащихся, что в случае отбора корней применение общей формулы серии решений для синуса и косинуса не является удобным. В этом случае удобнее не объединять серии решений, а представлять их совокупностью.
-
При повторении формул решения уравнений следует обратить внимание учащихся на то, что эти формулы задают множества чисел, которые образуют арифметические прогрессии с разностью
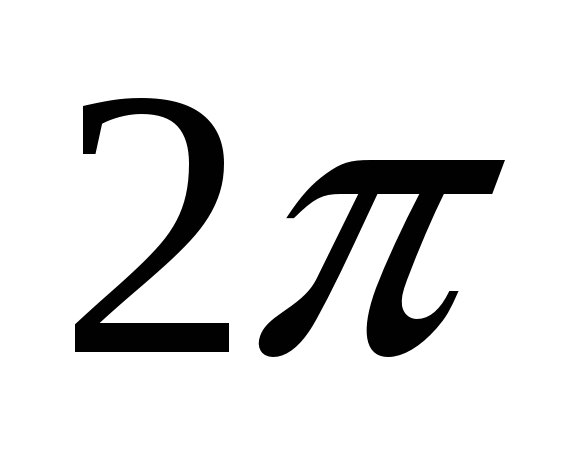 для синуса и косинуса и
для синуса и косинуса и  для тангенса и котангенса.
для тангенса и котангенса. -
Решения уравнений
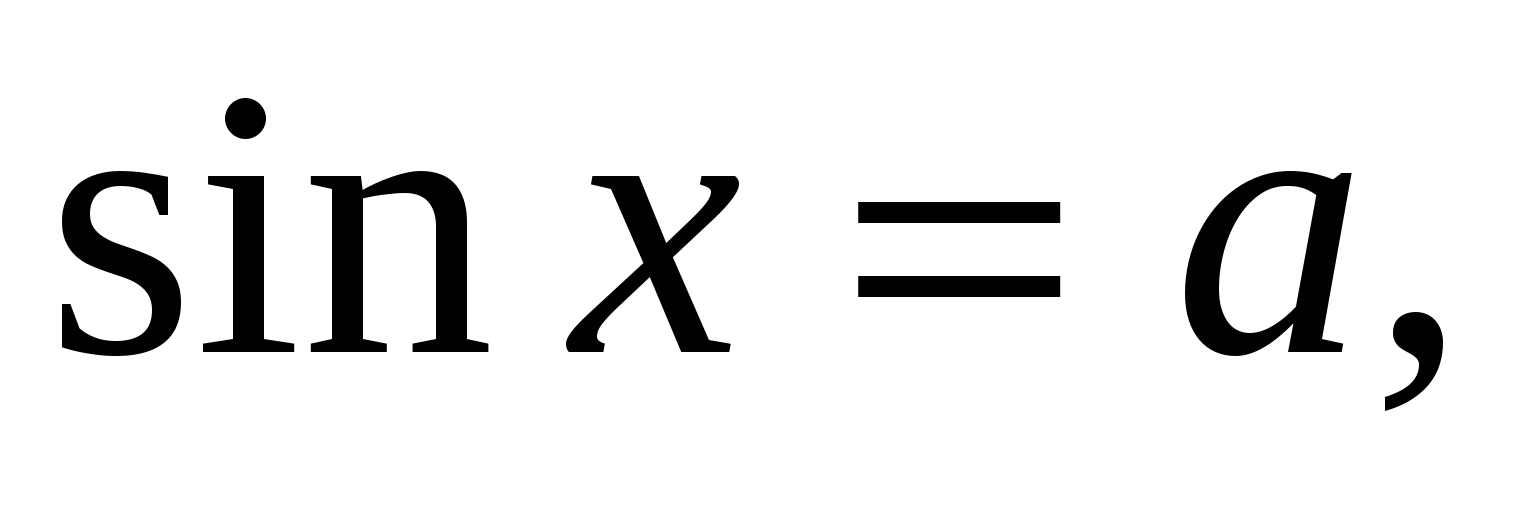 (
(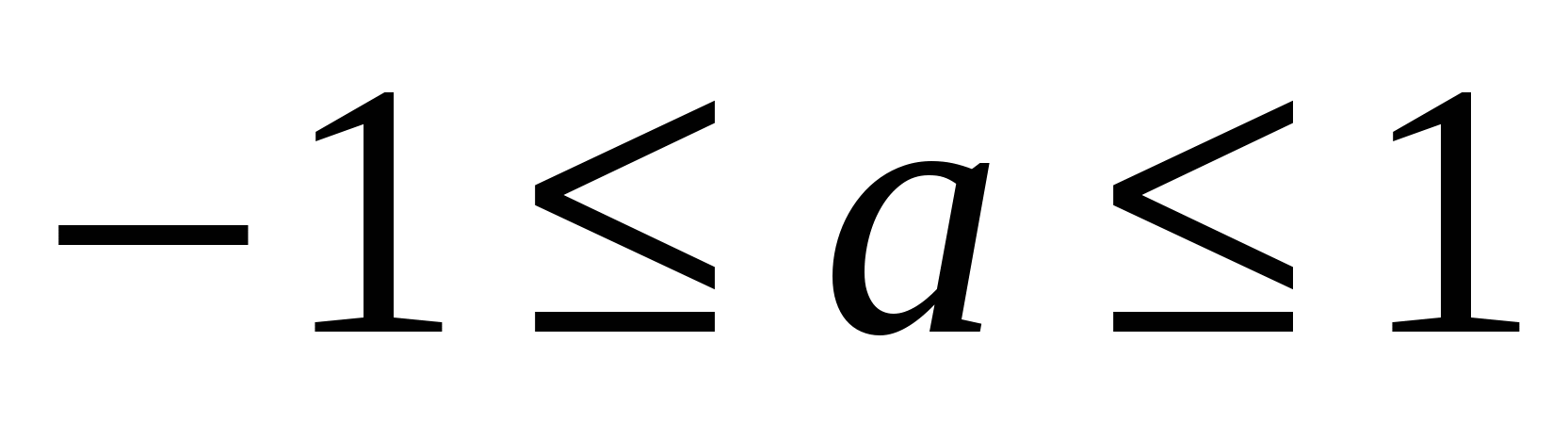 ) можно записать совокупностью двух серий решений:
) можно записать совокупностью двух серий решений:
![]()
![]()
Уравнения имеют решения:
|
|
| |
|
|
|
|
-
Решения уравнений
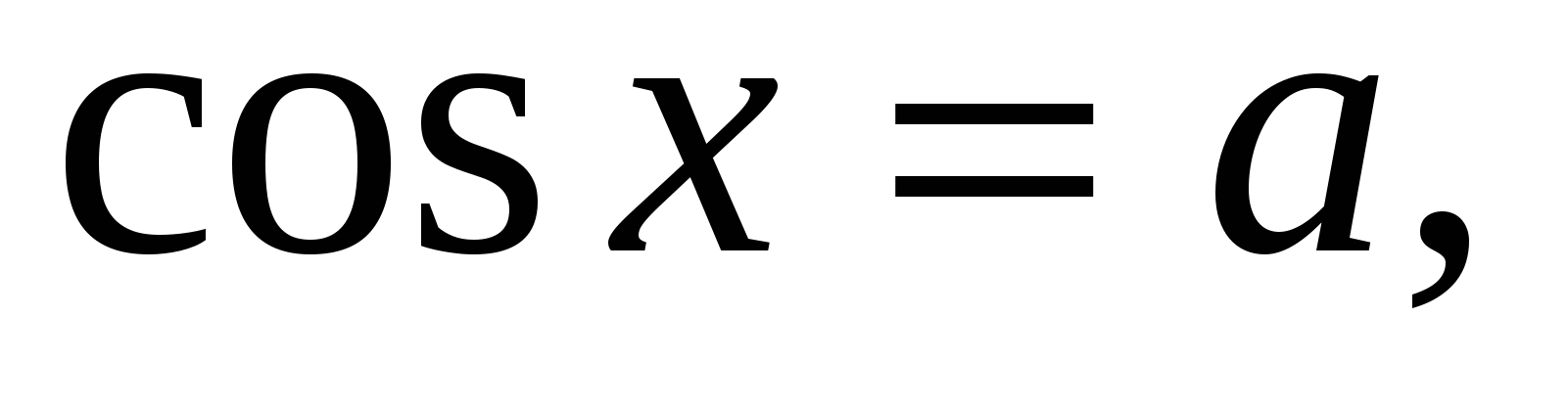 (
(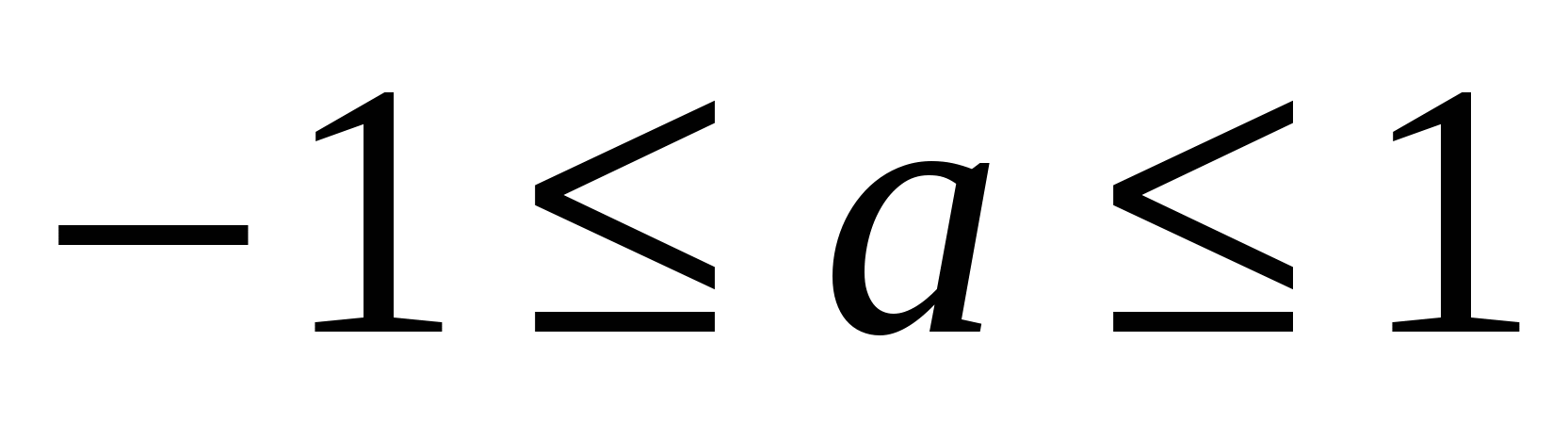 ) можно записать совокупностью двух серий решений:
) можно записать совокупностью двух серий решений:
![]()
![]()
Уравнения имеют решения:
|
|
| |
|
|
|
|
-
Решения уравнений
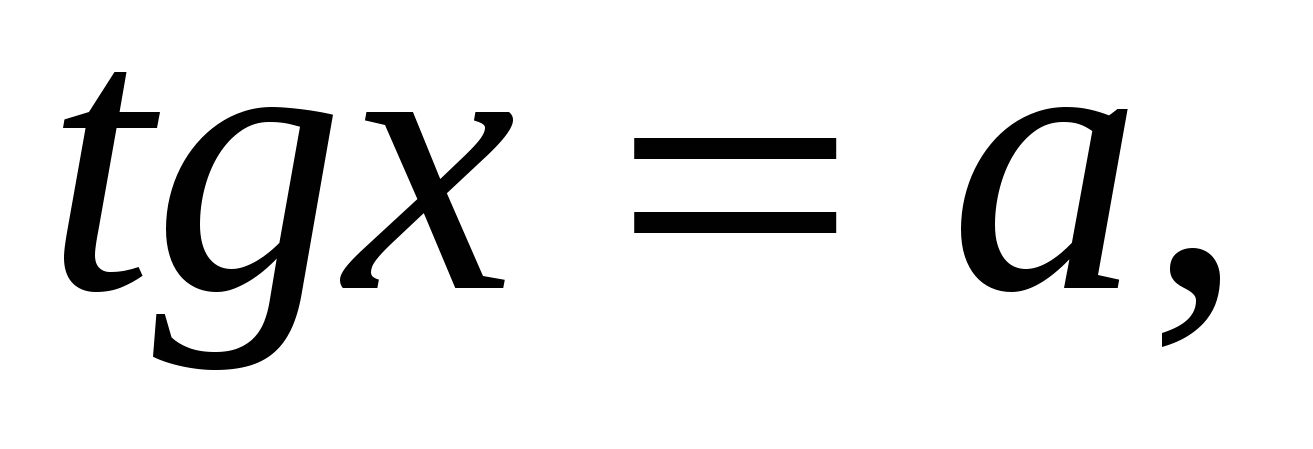 (
(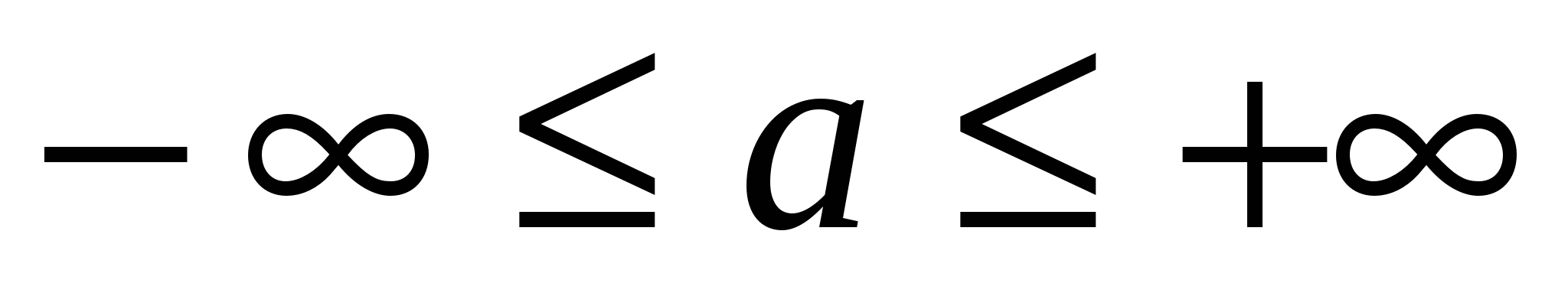 ) можно записать совокупностью двух серий решений:
) можно записать совокупностью двух серий решений:
![]()
![]()
Уравнения имеют решения:
|
|
| |
|
|
|
|
-
Решения уравнений
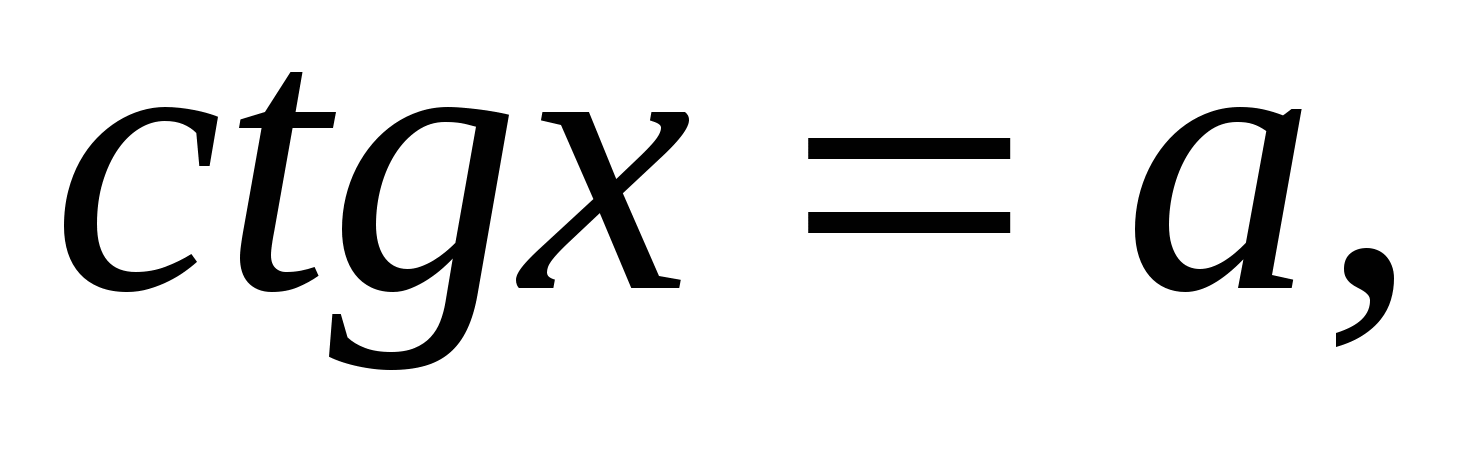 (
(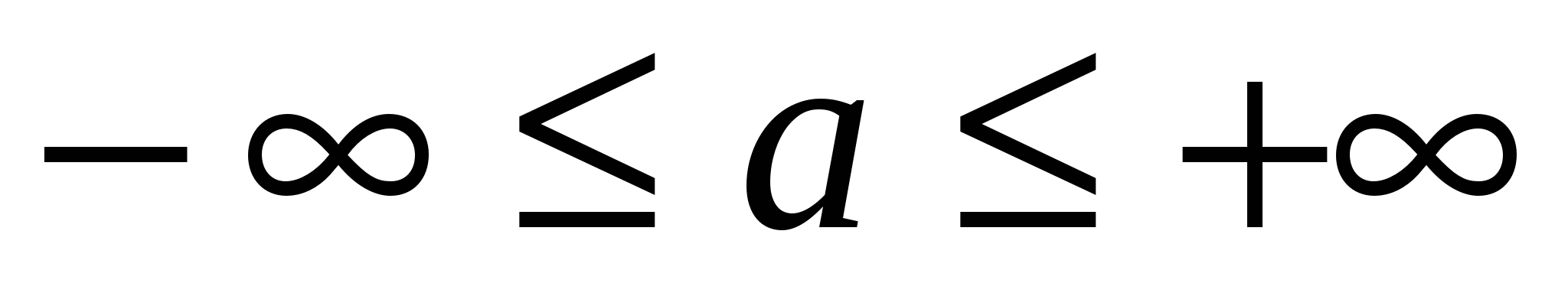 ) можно записать совокупностью двух серий решений:
) можно записать совокупностью двух серий решений:
![]()
![]()
Уравнения имеют решения:
|
|
| |
|
|
|
|
-
Арифметический способ отбора корней
При отборе корней в процессе решения тригонометрических уравнений обычно используют один из следующих способов: арифметический, алгебраический, геометрический, функционально-графический. Рассмотрим арифметический способ отбора корней. Данный способ отбора корней связан с вычислением корней при переборе значений целочисленного параметра или нахождением значений тригонометрических выражений непосредственной подстановкой при проверке корней.
Рассмотрим примеры, в которых используется арифметический способ отбора корней.
-
Непосредственная подстановка в уравнение и имеющиеся ограничения.
Пример 1. Решите уравнение:![]() .
.
Решение: ![]() . Это уравнение равносильно системе
. Это уравнение равносильно системе 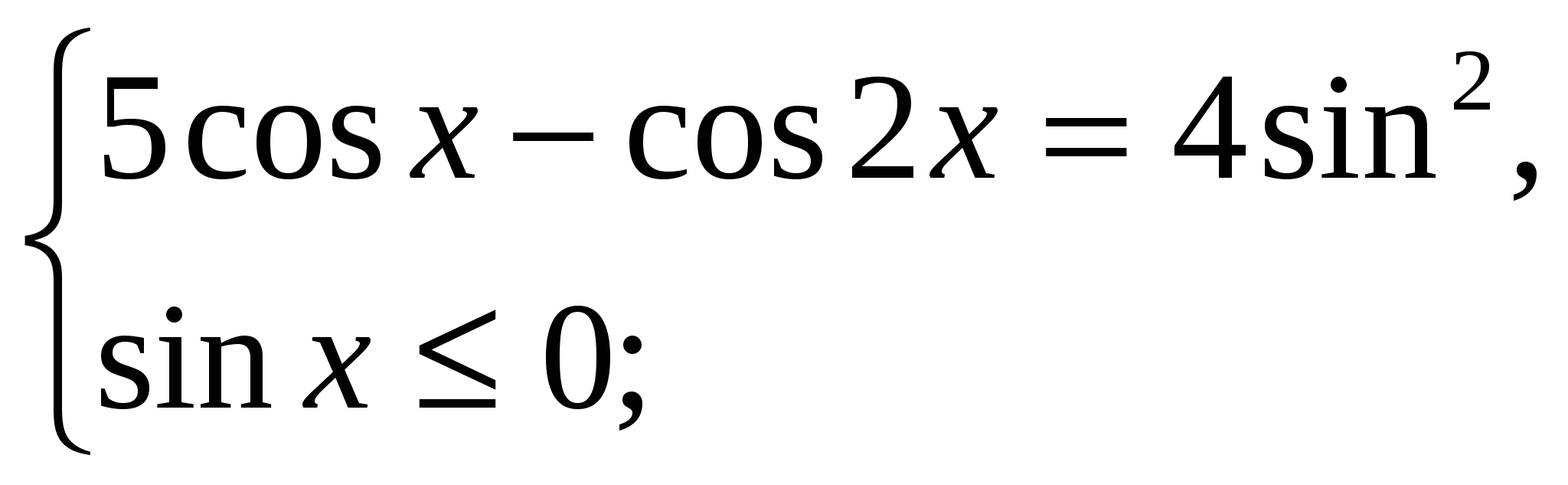 Решим уравнение системы:
Решим уравнение системы: 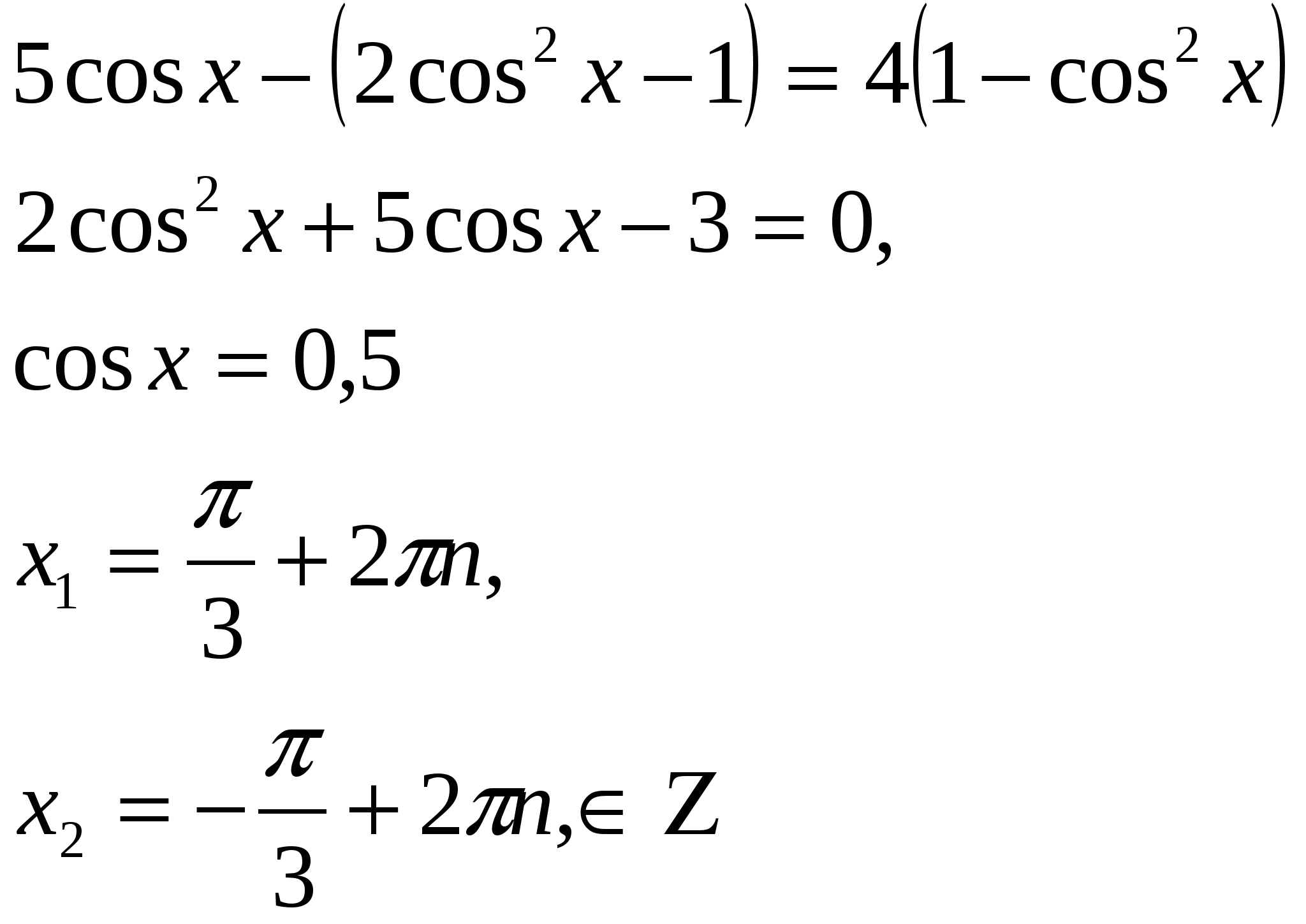 или
или ![]() корней нет
корней нет
Проверим для полученных значений х выполнение условия ![]() . Для первой серии получаем:
. Для первой серии получаем: ![]()
Следовательно, первая серия является «посторонней». Для второй серии получаем: ![]()
Следовательно, все числа второй серия решений уравнения системы являются корнями исходного уравнения.
Ответ: ![]()
Пример 2. Решить уравнение ![]()
Решение: Рассмотрим два множества значений неизвестной х, для которых ![]() и
и ![]() соответственно.
соответственно.
1. Пусть ![]() , тогда данное уравнение принимает вид:
, тогда данное уравнение принимает вид:
![]()
![]()
Разделив обе части уравнения на cos x (так как ясно, что cos x не равен нулю), получим:
![]()
![]() Из этой серии решений отберём значения х, для которых
Из этой серии решений отберём значения х, для которых ![]()
Подставляя значения ![]() в это неравенство, находим:
в это неравенство, находим: ![]() при к=2n,
при к=2n,
![]() при к=2n,+1.
при к=2n,+1.
Следовательно, корнями исходного уравнения являются числа вида ![]()
2. Пусть ![]() , тогда данное уравнения принимает вид:
, тогда данное уравнения принимает вид: ![]()
![]()
![]()
![]()
![]()
Отберём из полученных решений те значения х, для которых
![]() Подставляя значения
Подставляя значения ![]() в это неравенство, находим:
в это неравенство, находим:
![]()
![]()
Следовательно, корнями исходного уравнения являются числами вида ![]()
Ответ: ![]()
![]()
-
Учёт области определения или множества значений функций. Иногда при обобщении уравнений некоторые «посторонние» решения, возникающие в результате замены, могут быть удалены по причине несоответствия их области определения или множеству значений тригонометрических и обратно тригонометрических функций (таблица).
| Область определения | Область значений функции | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. Решите уравнение ![]()
Решение: Данное уравнение равносильна системе: 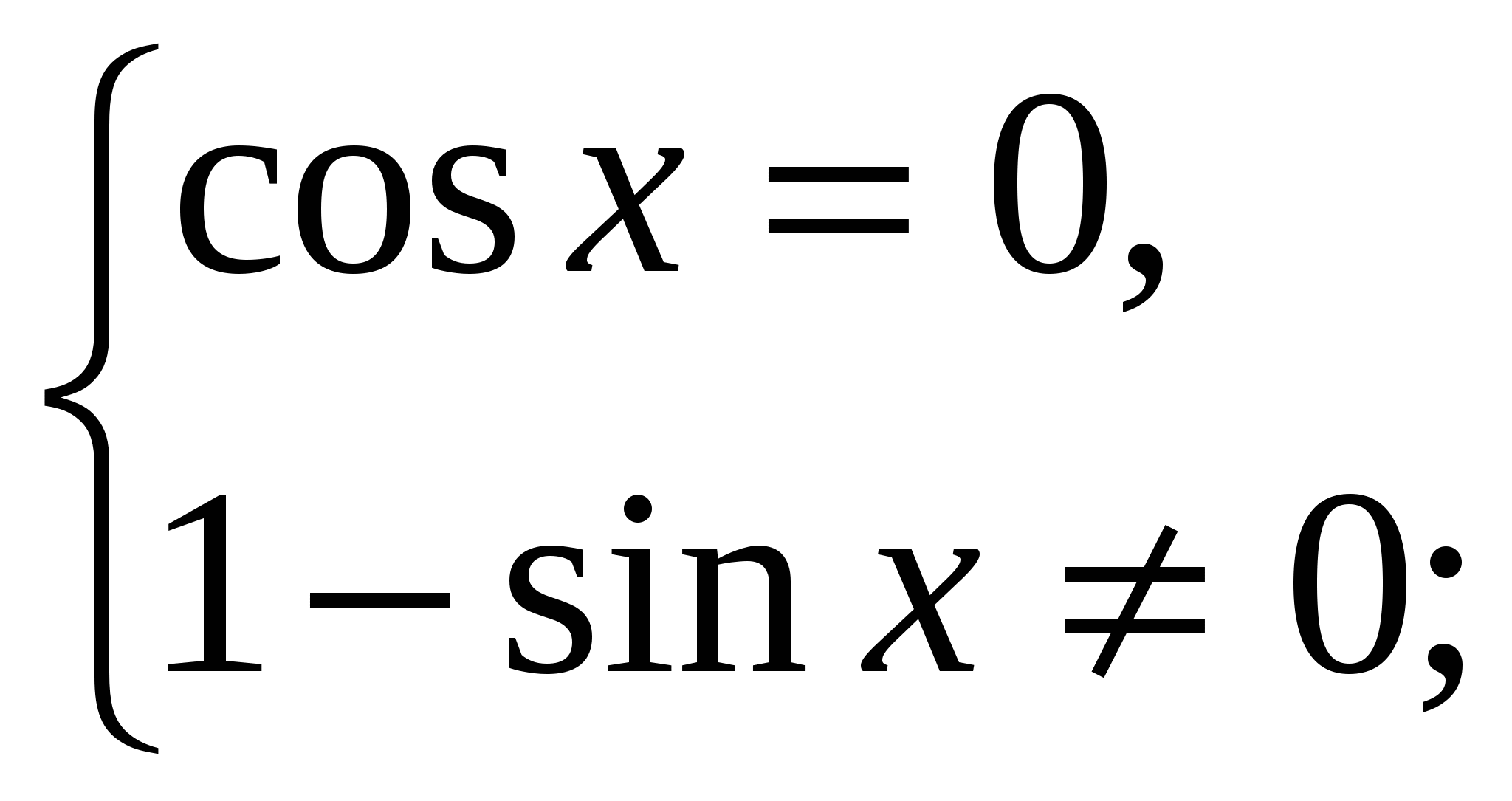
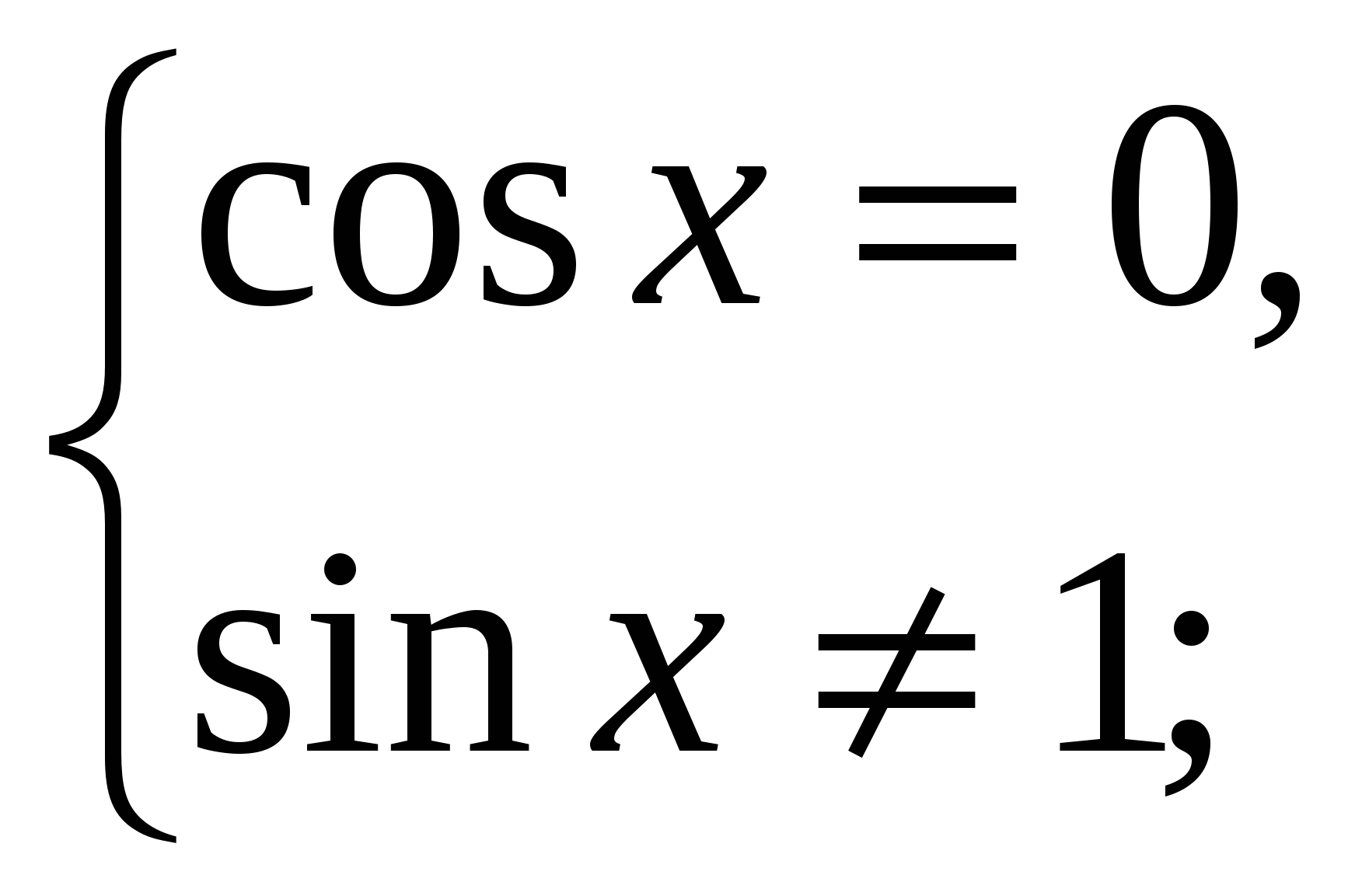
Если 0![]() , то (из основного тригонометрического тождества) sinx=1, или sinx=-1. Так как sinx не равен нулю, то остаётся отобрать те значения х, при которых sinx=-1. Отсюда
, то (из основного тригонометрического тождества) sinx=1, или sinx=-1. Так как sinx не равен нулю, то остаётся отобрать те значения х, при которых sinx=-1. Отсюда ![]()
Ответ: ![]()
Пример 2. Решить уравнение ![]()
Решение: Воспользовавшись формулой синуса двойного угла, получаем:
![]()
![]()
Так как ![]() при всех
при всех ![]() , то
, то ![]() Следовательно, уравнение равносильно системе:
Следовательно, уравнение равносильно системе: 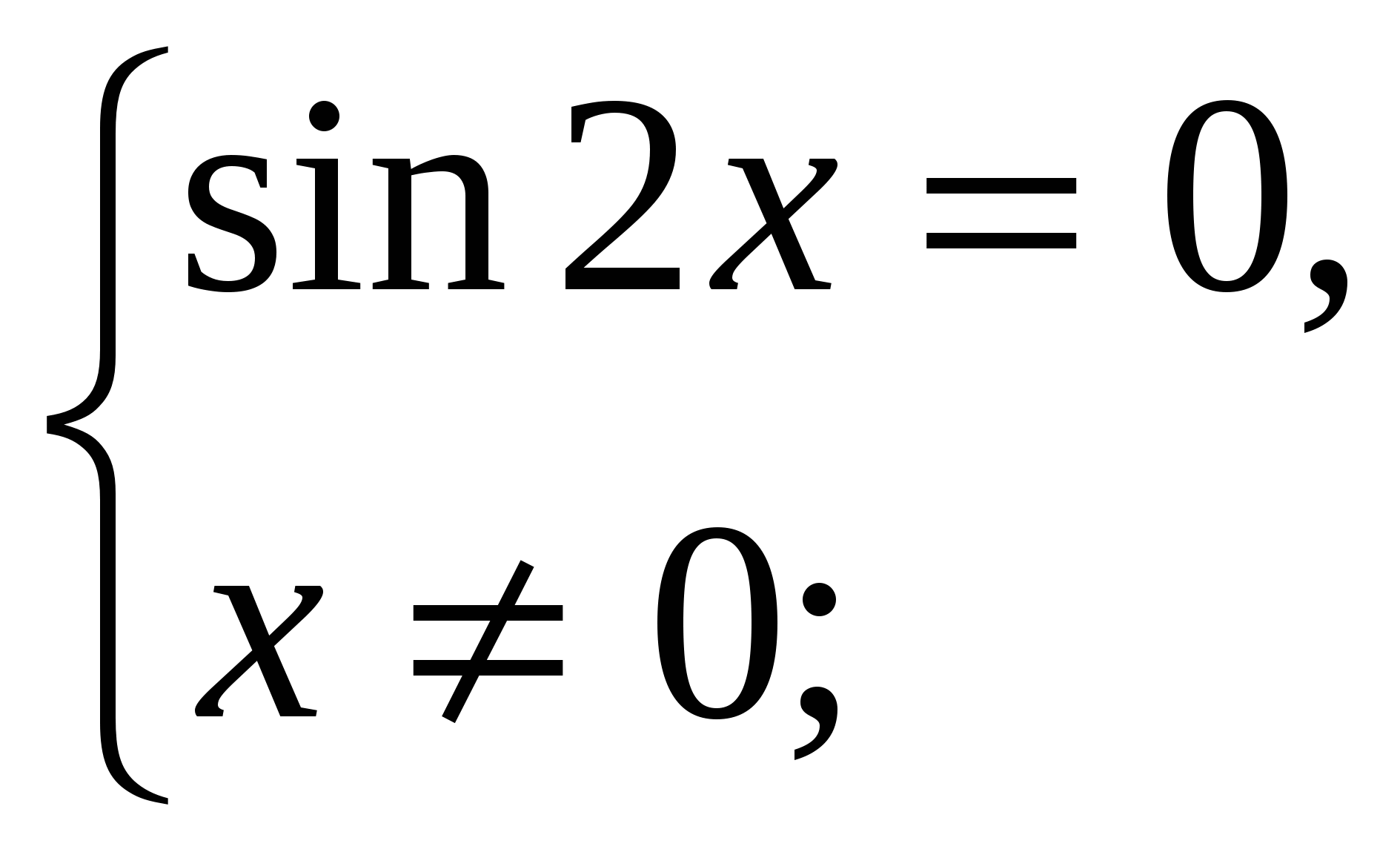 отсюда
отсюда ![]()
Ответ: ![]()
-
Подведение итогов урока.
-
Домашнее задание.
1. Найдите корни уравнения ![]() удовлетворяющих неравенству
удовлетворяющих неравенству ![]()
Решите уравнения:
2. ![]()
3. ![]()
4. ![]()
5. ![]()
Здесь представлен конспект к уроку на тему «Арифметический способ отбора корней в тригонометрических уравнениях», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

