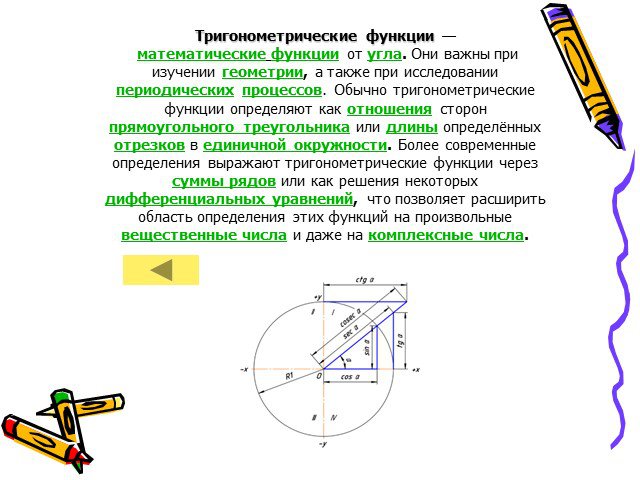
Презентация "Тригонометрические функции" по математике – проект, доклад
Презентацию на тему "Тригонометрические функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
Тригонометрические функции углов в произвольном треугольнике 1-2
Продолжите фразу:. Синусом острого угла прямоугольного треугольника называется. А С В. отношение противолежащего катета к гипотенузе. Косинусом острого ...Тригонометрические функции углового аргумента - алгебра,
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Тригонометрические функции углового аргумента
Цель урока: отработка навыка нахождения значений тригонометрических функций углового аргумента. Задачи: 1.обобщить и систематизировать учебный материал ...Тригонометрические функции одного и того же аргумента
Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной ...Тригонометрические функции угла
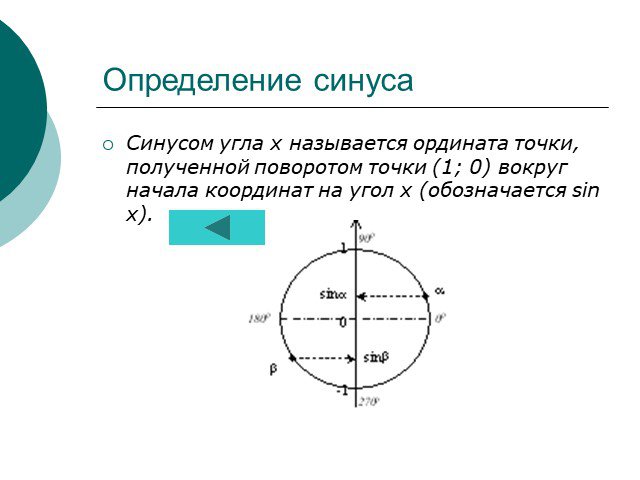
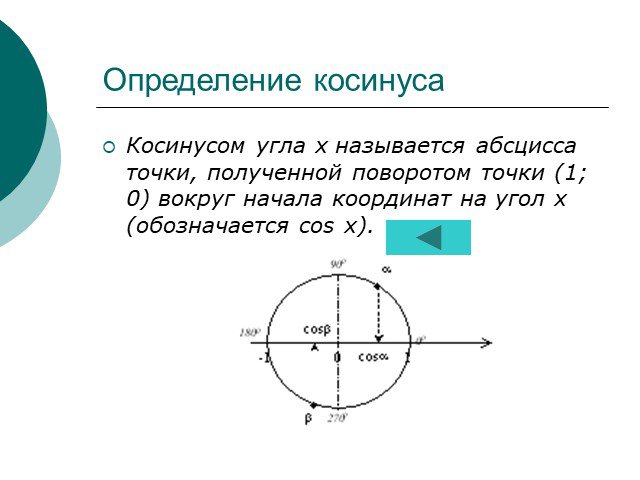
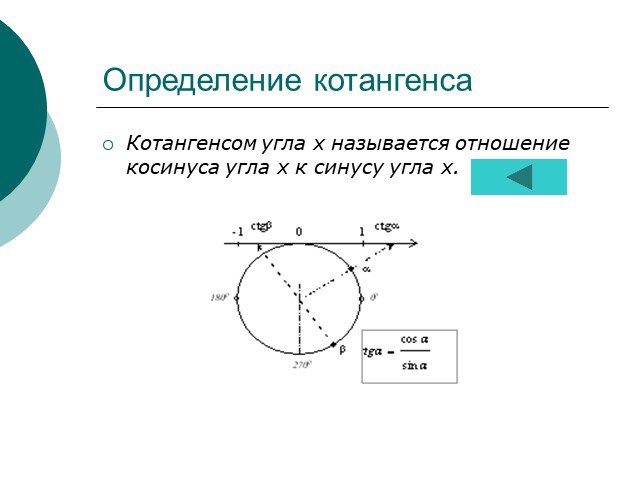
Что такое косинус угла ? Это число, которое можно определить следующим образом:. cos α ≈ 0,4 1 0 -1. В прямоугольной системе коодинат. проводим полуокружность. ...Тригонометрические функции
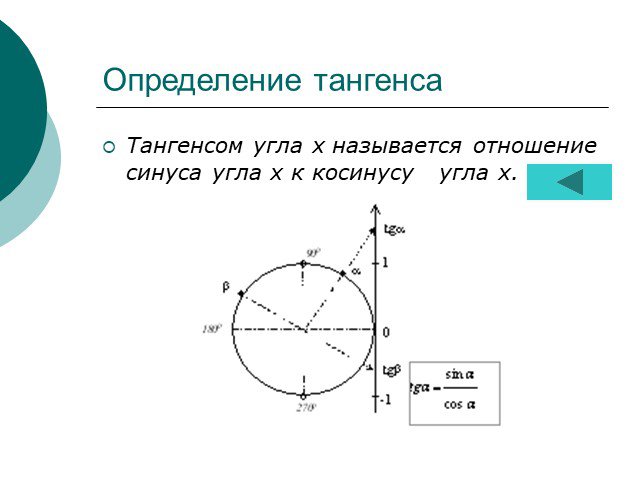
Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника 1) Синус - отношение противолежащего катета ...Тригонометрические функции и их свойства
Системы счисления. Память человечества не сохранила, не донесла до нас имя изобретателя колеса или гончарного круга. Это и не удивительно: более 10 ...Тригонометрические функции числового аргумента
- вычисление значений тригонометрических функций; - упрощение тригонометрических выражений. Цель урока. Нужно знать:. - определения тригонометрических ...Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа.
1. У = - f(x) ← y = f(x) , симметрия относительно оси ОХ. 2. У = f(- x) ← y = f(x), симметрия относительно оси ОУ. 3. У = - f (- x) ← y = f(x), симметрия ...Тригонометрические функции
Числовая окружность. 1. 2. М • В С D 4. А + –. у. На макетах обозначены лишь главные имена точек – числа, принадлежащие но у точек на окружности бесконечное ...Основные тригонометрические функции
Пояснительная записка. В результате изучения курса математики учащиеся должны понимать, что функция – математическая модель, позволяющая описывать ...Обратные тригонометрические функции
Историческая справка. Тригонометрические функции возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике ...Обратные тригонометрические функции
Содержание: Обратные тригонометрические функции, свойства, графики Историческая справка Преобразование выражений, содержащих обратные тригонометрические ...Уравнения, содержащие обратные тригонометрические функции
1.Выразить через функцию от х:. 2.Вычислить: а) б) 4.Упростить:. 3.Найти область определения функции. Т-3. Выразить arcsinx через другие функции. ...Обратные тригонометрические функции
15.05.2019. I. Математический диктант. 1)D(y)= 2)E(y)= 3) 4)sin(-x)=-sin x 5)Возрастает на Убывает на 6)Периодичная. I вариант y=sin x II вариант ...Преобразование графика квадратичной функции
Проверка результатов исследований. 1 группа (y=x2+c) y=x2+3;. С=3 – сдвиг вверх по оси ординат на 3. 2 группа (y=x2+c) y=x2-5;. С=-5 – сдвиг вниз ...Тригонометрические формулы
Цель урока. Повторить и систематизировать изученный материал Подготовиться к контрольной работе. Задачи урока. Повторить определение синуса, косинуса, ...График степенной функции
Эпиграфом нашего урока являются слова А. Эйнштейна:. “Весь наш предшествующий опыт приводит к убеждению, что природа является осуществлением того, ...Степенные функции
“СТЕПЕННЫЕ ФУНКЦИИ” Степенная функция с нечетным натуральным показателем. Корень нечетной степени. Степенная функция с четным натуральным показателем. ...Тригонометрические уравнения
I. Повторение и актуализация. 1. Что значит простейшая тригонометрическая функция? 2. Приведите пример простейшего тригонометрического уравнения. ...Конспекты
Тригонометрические функции острого угла
МКОУ СОШ с.п.Кара-Суу Черекского района КБР. Айшаева Фердаус Сулеймановна. . "Тригонометрические функции острого угла" Геометрия 8 класс. ...Функции. Тригонометрические функции
Учитель математики ГБОУ СОШ № 230 с углубленным изучением химии и биологии. Ваганова Г. В. Тема. :. . « Функции. Тригонометрические ...Тригонометрические функции
Урок по теме:. «. Тригонометрические функции. ». 10 класс. Составитель - учитель математики Апарина Е.Г. с. Майкопское. ...Тригонометрические функции числового аргумента
Название работы: Урок с использованием готовых электронных образовательных ресурсов. . Автор (авторы):. Чуракова Нина Анатольевна(. chura. -. nina. ...Обратные тригонометрические функции
Разработка урока по теме: «Обратные тригонометрические функции». 10 класс. Тип урока. : изучение нового материала. Цели урока. :. обучающие. ...Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции
Конспект урока по алгебре и началам анализа по теме. «Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции». . ...Тригонометрические преобразования
Конспект. элективного занятия в 10 классе. 19.11.08. Тема: Тригонометрические преобразования. Цель:. . Повторение основного тригонометрического ...Степени и корни. Степенные функции
Поурочные разработки. по. . алгебре и началам анализа к УМК А.Г. Мордковича 11 класс. Глава 6. . Степени и корни. Степенные функции. . Урок ...График квадратичной функции и модуль
Администрация города Улан - Удэ. Комитет по образованию. МАОУ «Средняя общеобразовательная школа № 25». Урок алгебры в 9 классе. ...Применение производной к исследованию функций. Наибольшее и наименьшее значение функции
ГОУ «Школа здоровья и индивидуального развития». Красногвардейского района. Санкт-Петербурга. Урок алгебры и начал анализа. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Петрова Анастасия
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию