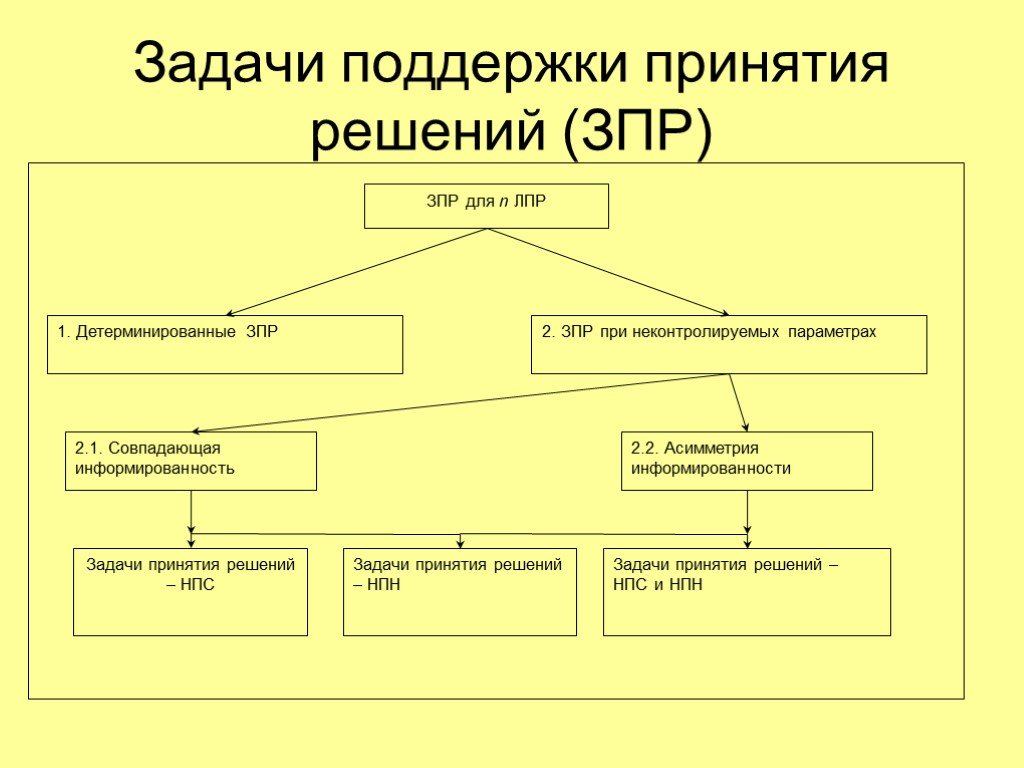
Презентация "Задачи поддержки принятия решений (ЗПР)" по математике – проект, доклад
Презентацию на тему "Задачи поддержки принятия решений (ЗПР)" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 28 слайд(ов).
Слайды презентации
Список похожих презентаций
Задачи практической направленности
В городе N живет 100000 жителей. Среди них 15 % детей и подростков. Среди взрослых 45% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько ...Задачи с целыми числами
Бабушка Миши собралась стряпать пирог, и ей не хватало яблок, бананов и немного клубники. Она попросила Мишу купить 6 яблок, 6 бананов и 12 ягод клубники. ...Задачи на цену, количество, стоимость
УРОК МАТЕМАТИКИ С ЭЛЕМЕТАМИ ЭКОНОМИКИ. 3 класс (программа М.И.Моро). Учитель начальных классов Пономаренко Людмила Викторовна. Тема: Решение задач ...Задачи по вписанной и описанной окружности
Теорема 1. Около всякого треугольника можно описать окружность. Ее центр является точкой пересечения серединных перпендикуляров к сторонам треугольника. ...Задачи на сложение и вычитание дробей
Чтобы сложить (вычесть) десятичные дроби, нужно:. Записать дроби так, чтобы запятая была под запятой; Уравнять количество знаков после запятой; Выполнить ...Задачи на составление уравнений
Цели урока. закрепление вычислительных навыков; закрепление умений решения уравнений; формирование умений решения текстовых задач путем выделения ...Задачи В8. Подготовка к ЕГЭ
На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции ...Задачи на проценты.
Ключевые задачи на проценты 1) Нахождение процента от числа. Чтобы найти процент от числа нужно: - выразить процент обыкновенной или десятичной дробью; ...Задачи в два действия
Цели и задачи. 1) Уточнить термины, связанные с понятием «задача»: условие, вопрос, выражение, решение, ответ. 2) Научить делать краткую запись задач ...Задачи в координатах
Цели урока:. Образовательная; Развивающая; Воспитательная. Образовательная:. Отработка навыков и умений решения простейших задач в координатах и решения ...Задачи «Четырехугольники»
Выберите фигуры, которые относятся к понятию «четырехугольник». верно неверно. Внимание! В нашем городе произошел ряд таинственных происшествий. Раскрыть ...Задачи
Кого из животных нужно взять с собой крестьянину? Первый шаг: крестьянин перевозит козу. Второй шаг: крестьянин возвращается назад. Третий шаг: крестьянин ...Доли. Задачи Г. Остера
Коля и Оля разделили яблоко пополам и увидели, что это яблоко собирались есть ещё два червяка. Коля отделил от своей части яблока половину и уступил ...Подготовка к ЕГЭ - 2017 "Задачи по стереометрии"
Задача №1. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса. Задача №2. Во сколько раз увеличится ...Задачи военно-прикладного характера
Замечательный квадрат. Задача. Великая Отечественная война началась 22 июня 1941 года. Узнать, сколько дней продолжалась война, поможет вам удивительный ...Задачи на проценты
Цель урока:. обобщение и систематизация знаний по теме «Проценты»; повторить перевод процентов в десятичные дроби и наоборот; усвоение практической ...Задачи группы В 12
Схема решения задач на движение и На совместную Работу.Уметь строить и исследовать простейшие математические модели. Задачи на движение. От станции ...
Задачи на разрезание
Основная цель:. познакомить учащихся с задачами на разрезание; развитие пространственного представления и логического мышления, интуиции и смекалки. ...Задачи для 1 класса
Я слышу – и забываю, Я вижу – и запоминаю,. Я делаю – и понимаю. Китайская мудрость. Веселые задачи. Мотыльки васильки. Вот синеют у реки Чудо-диво ...Задачи на совместную работу
. СОТРУДНИЧЕСТВО. Задачи на совместную работу. (урок 3) 5 класс. Учитель математики и информатики Забудько Ольга Николаевна. 2016 год. МБОУ ГСШ №1 ...Конспекты
Девять решений геометрической задачи
Муниципальное бюджетное общеобразовательное учреждение. «Верхнеуслонская средняя общеобразовательная школа». Верхнеуслонского муниципального района ...Задачи на увеличение числа на несколько
Урок математики в 1 классе. Тема урока:. Задачи на увеличение числа на несколько единиц. (с двумя множествами предметов) УМК «Школа России». Целеполагание ...Задачи на сравнение
ОС «Школа 2100», учебник «Математика-2 ч.» Л.Г. Петерсон. МАТЕМАТИКА, 1 класс. ТЕМА. Задачи на сравнение. ЦЕЛЬ:. . учить решать задачи на ...Задачи на смеси, проценты, пропорции
Решение текстовых задач. Решение текстовых задач вызывает наибольшие. затруднения учащихся? Поэтому руководствуюсь следующим:. Чтобы научить ...Задачи на разностное сравнение
Тема:. «Задачи на разностное сравнение». Основные цели:. - помочь усвоить правила разностного сравнения чисел, ввести схему из отрезков для моделирования ...Задачи на разностное сравнение
Технологическая карта урока математики. Дидактическое обоснование:. «Математика 1 класс» (2 часть) М.И. Моро, С.И. Волкова, С.В. Степанова, УМК ...Усвоение таблицы умножения числа 8. Задачи на приведение к единице
Тема:. Усвоение таблицы умножения числа 8. Задачи на приведение к единице. Цели. : учащиеся научатся сравнивать задачи первого и второго вида на ...Задачи, решаемые составлением системы уравнений
9 класс алгебра. Тема урока. : « Задачи, решаемые составлением системы уравнений». Учебно-воспитательные задачи:. 1). Сформировать модель алгоритма ...Задачи на встречное движение
Конспект урока по математике. Тема урока:. Задачи на встречное движение. Тип урока:. открытие новых знаний. Цель урока:. способствовать развитию ...Задачи и загадки
МОУ «Теньковская средняя общеобразовательная школа». Камско-Устьинского муниципального района РТ. Методическая разработка. урока математики ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 октября 2019
Категория:Математика
Содержит:28 слайд(ов)
Поделись с друзьями:
Скачать презентацию