Презентация "Степенные функции" по математике – проект, доклад
Презентацию на тему "Степенные функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 31 слайд(ов).
Слайды презентации
Список похожих презентаций
Степенные функции с отрицательным целым чётным показателем
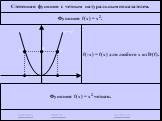
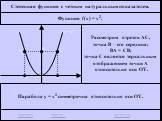
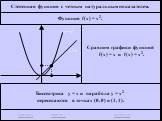
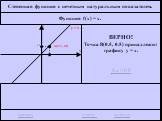
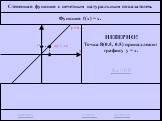
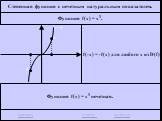
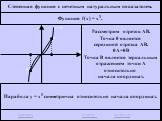
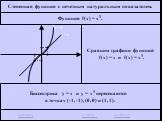
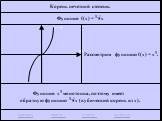
повторение. График какой функций изображен на рисунке. (данный график построен из графика функции ) Прочитайте данный график. Ни чётная, ни нечётная. ...Тригонометрические функции углов в произвольном треугольнике 1-2
Продолжите фразу:. Синусом острого угла прямоугольного треугольника называется. А С В. отношение противолежащего катета к гипотенузе. Косинусом острого ...Степенные ряды. Область сходимости степенного ряда
Содержание:. Определение степенного ряда Примеры степенных рядов Область сходимости степенного ряда. 4. Равномерная сходимость функционального ряда. ...Свойства функции
. Монотонность. Возрастающая Функцию у = f(х) называют возрастающей на множестве Х, если для любых двух точек х1 и х2 множества Х, таких, что х1 < ...Свойства и график логарифмической функции
- 5 - 4 - 3 - 2 -1 0 1 2 3 4 5 4 3 2 1 -1 -2 -3 -4. D(f)= E(f)= y=0 при х= y>0 при х y. Логарифмическая функция, её свойства и график. Опр. Логарифмической ...Производная показательной функции
www.thmemgallery.com Company Logo План урока. Устная работа. Определение производной. Правила дифференцирования. Производные элементарных функций. ...Преобразования графиков квадратичной функции
Квадратичной функцией называется функция вида у = ax²±bx±c Например : у=2x²+3x-4, а=2, b=3,c=-4 Графиком квадратичной функции является парабола Для ...Построение графика функции методом ее исследования с помощью производной
доцент кафедры математического образования Батан Любовь Федоровна. учитель математики первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя ...Взаимное расположение графиков линейной функции
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Взаимно обратные функции
Задача. у = f (x), x - ! Найти значение у при заданном значении х. Задача. у = f (x), у- ! Найти значение х при заданном значении у. Дано: у = 2х ...Взаимно обратные функции
Цель проекта: Изучить поведение взаимно обратных функций. Установить связь графиков прямой и обратной функций. Подготовиться к успешной сдаче ЕГЭ. ...Алгоритмы построения графиков функции
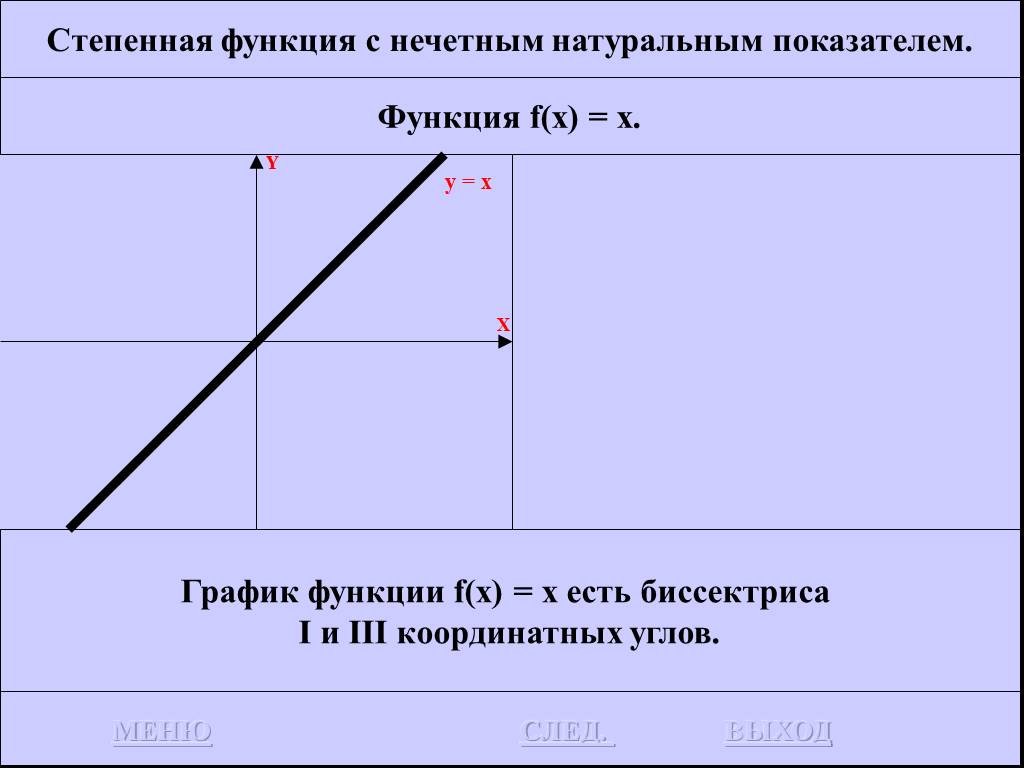
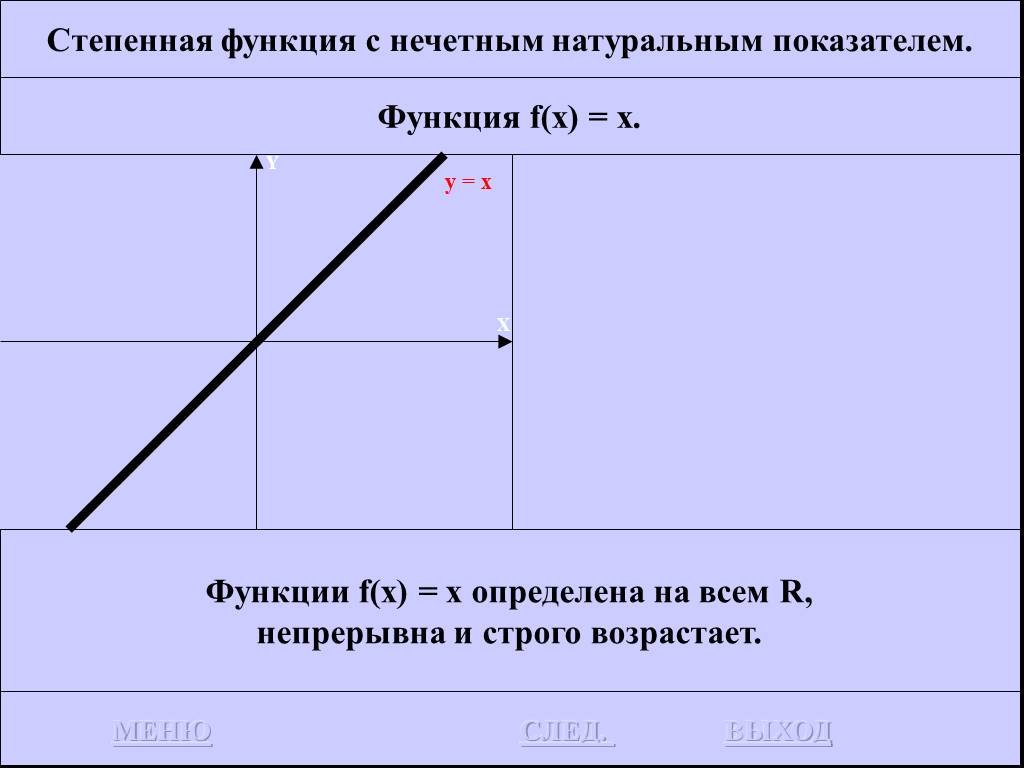
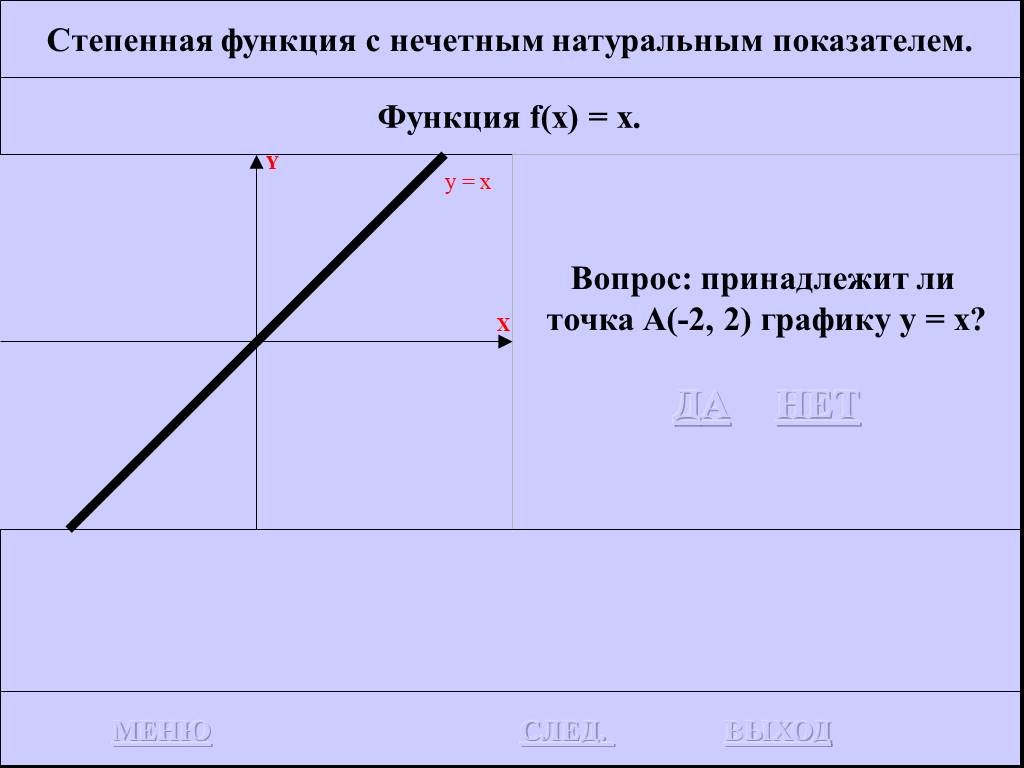
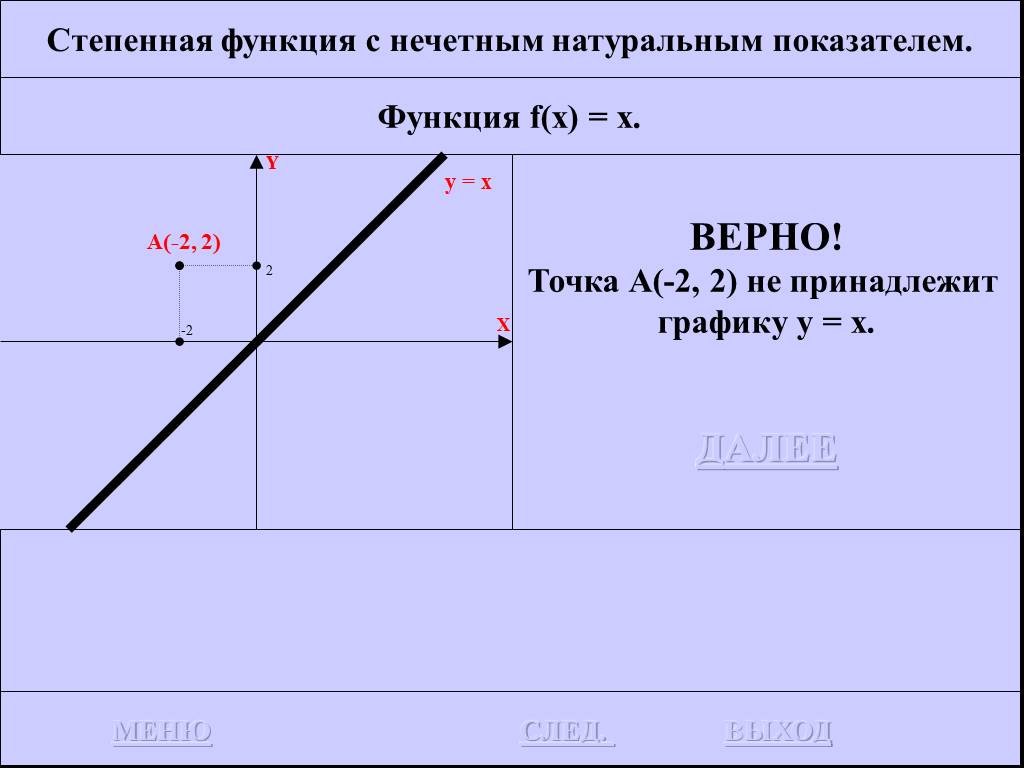
График функции у = |х| а) Если х≥0, то |х| = х функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х. Построить ...Алгоритмы - их функции и виды
Разветвляющийся алгоритм. Сюда пойдешь – клад найдешь. Сюда пойдешь – жену найдешь. Сюда пойдешь – мегабайт найдешь. Составить блок-схему алгоритма ...Алгоритм построения графика квадратичной функции
1)направление «ветвей» параболы. если а>0, то «ветви» параболы направлены вверх; если а 0 - «ветви» параболы направлены вверх;. 2)Нахождение координат ...Урок производная сложной функции
Найдите производные функций:. Найдите угловой коэффициент касательной, проведенной к графику функции. в его точке с абсциссой. Точка движется прямолинейно ...Экстремум функции
Точка х1 называется точкой минимума функции f(x), если в некоторой окрестности точки х1 выполняется неравенство. Значения функции в точках х0 и х1 ...Влияние коэффициентов а, b и с на расположение графика квадратной функции
Определите, график какой функции изображен на рисунке:. у = х² – 2х – 1; у = –2х² – 8х; у = х² – 4х – 1; у = 2х² + 8х + 7; у = 2х² – 1. у = ½х² – ...Предел функции в точке
Одна и та же кривая, три разные функции. Отличие – поведение в точке х = а. f(a) – не существует, т.к. в точке х =а функция у = f(х) не определена. ...Возрастание и убывание функции
Числовые промежутки. [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал. Функция f(x) называется возрастающей на некотором ...Применение производной функции
с и л а. в у м е. I вариант II вариант Буква С Буква В. Буква И Буква У. Буква Л Буква М. Буква А Буква Е 7. Сложилась фраза. ...Конспекты
Степени и корни. Степенные функции
Поурочные разработки. по. . алгебре и началам анализа к УМК А.Г. Мордковича 11 класс. Глава 6. . Степени и корни. Степенные функции. . Урок ...Степенные функции, их свойства и графики
Конспект урока на тему. «Степенные функции, их свойства и графики». Учитель. : Чижова Светлана Анатольевна г. Иваново. Тип урока:. урок формирования ...Степенные функции, их свойства и графики
Тема урока:. . «Степенные функции, их свойства и графики». . Цели урока:. . Образовательная:. Создать условия для закрепления знаний о свойствах ...Свойства линейной функции
Государственное бюджетное образовательное учреждение. средняя общеобразовательная школа №200 с углубленным изучением финского языка. Красносельского ...Производная сложной функции
Открытый урок. . по теме: «Производная сложной функции». . . Тип урока:. комбинированный. Цели:. образовательная:. - формирование умения ...Производная показательной и логарифмической функции
КГУ «Средняя школа №7 города Зыряновска». «Производная показательной и логарифмической функции». Учитель: ...Применение производной к исследованию функции
МОУ Греково-Степановская СОШ. . Чертковского района Ростовской области. Учитель математики и информатики. Киселева Лариса Анатольевна. Урок алгебры ...Признаки возрастания и убывания функции
Султанова Эльмира Хайкеновна. . КГУ «Колледж сферы обслуживания города Петропавловска», СКО г. Петропавловск. . Преподаватель математики. ...Предел функции в точке
Урок алгебры в 10 классе по теме «Предел функции в точке». Цель урока:. формирование у учащихся наглядно – интуитивных представлений о пределе ...Чётные и нечётные функции
Форма плана конспекта урока. План-конспект урока. «Чётные и нечётные функции». 1.ФИО (полностью) - Сороковикова Ирина Георгиевна. 2.Место работы ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 января 2019
Категория:Математика
Содержит:31 слайд(ов)
Поделись с друзьями:
Скачать презентацию




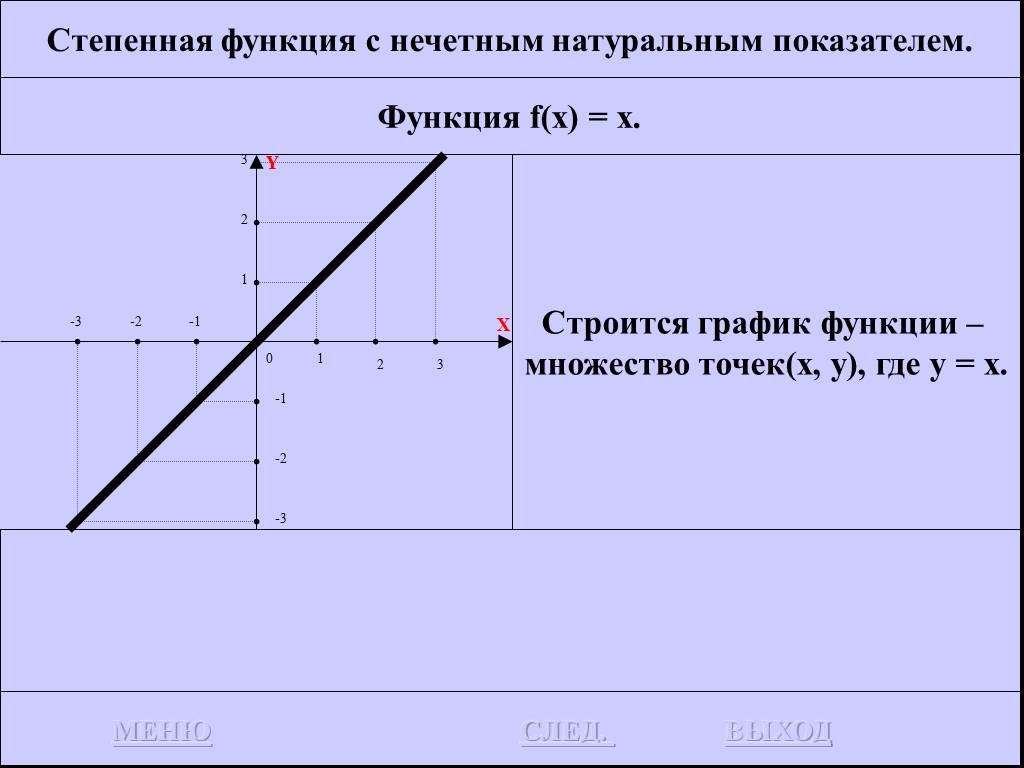
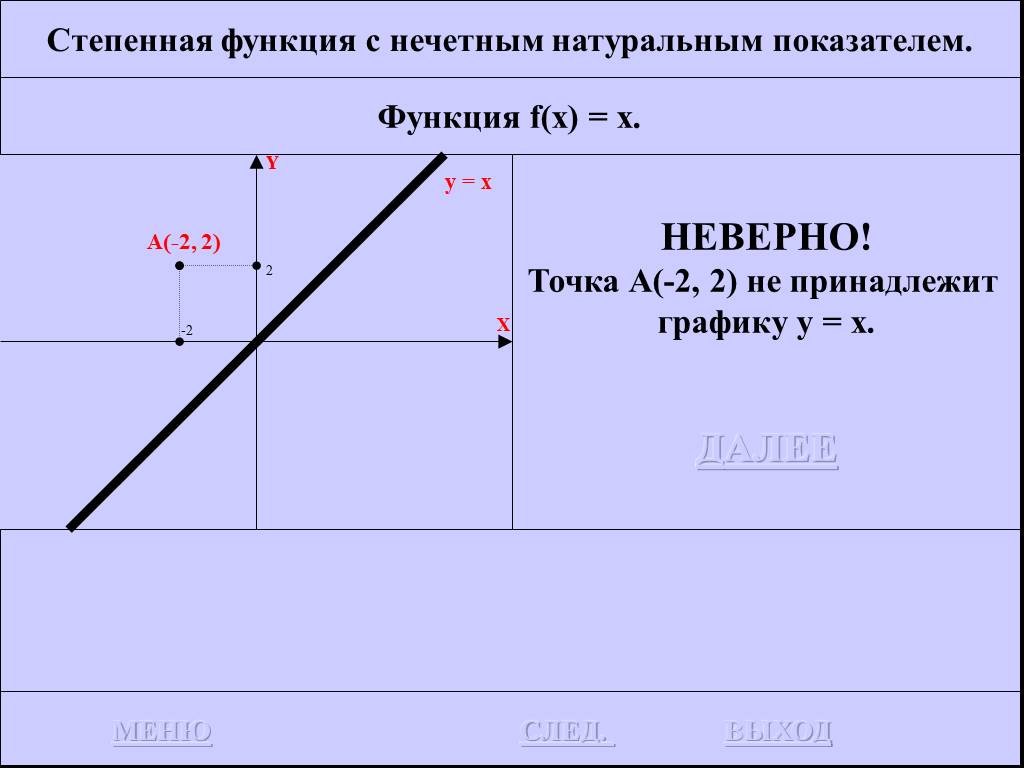
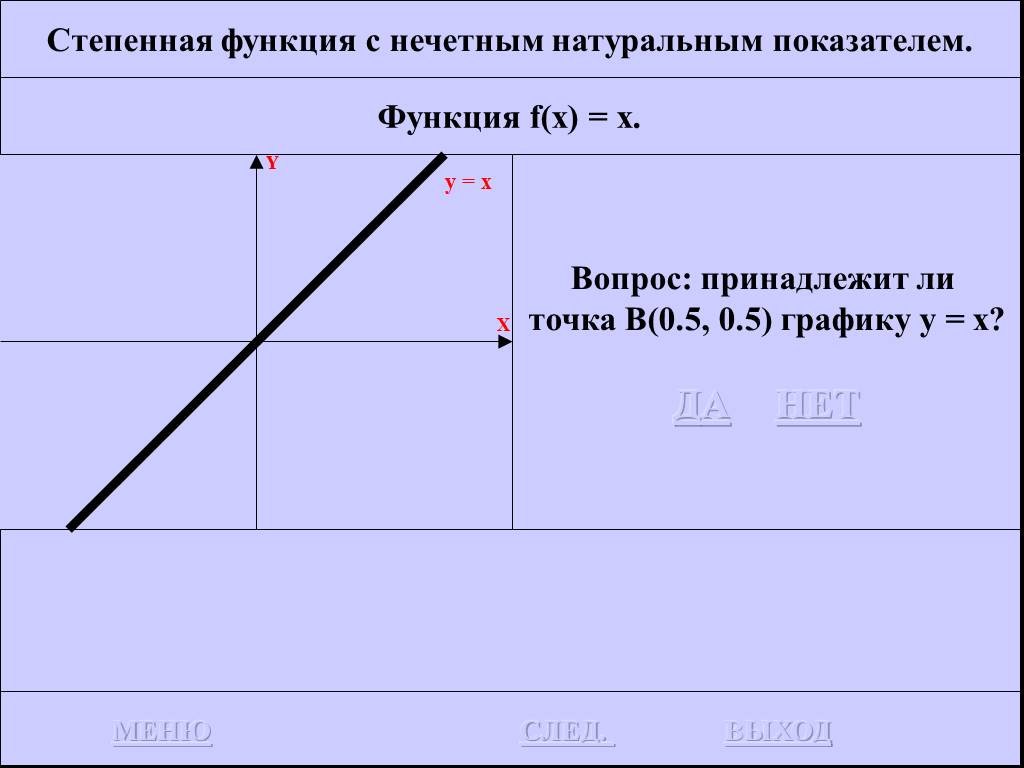
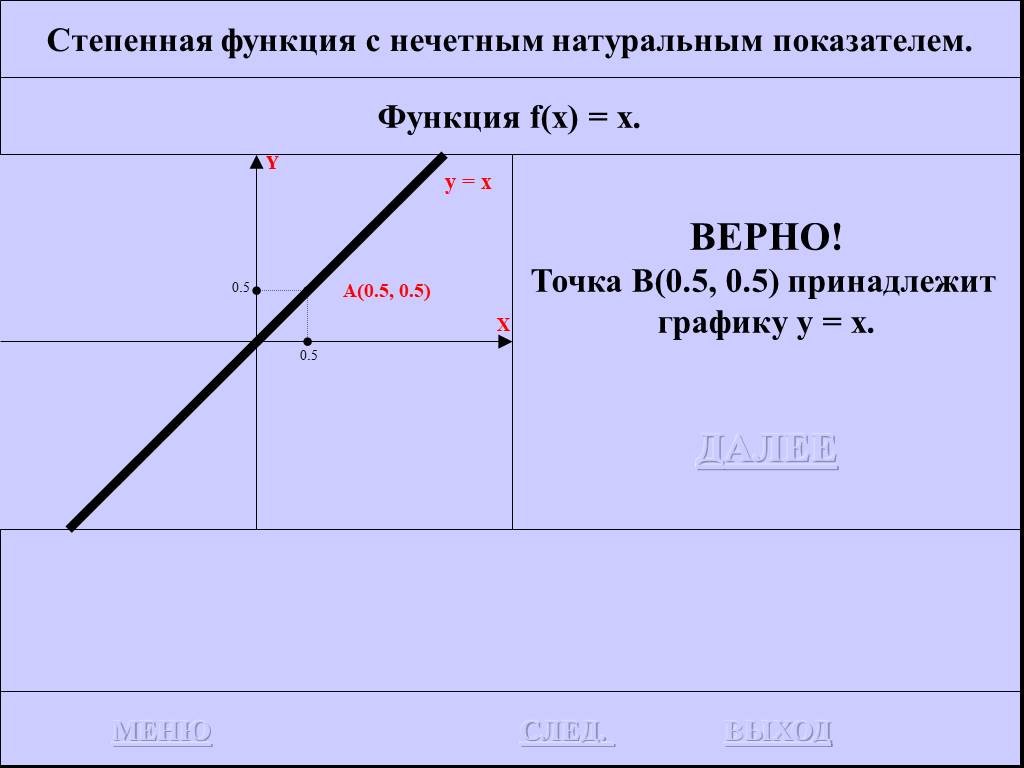
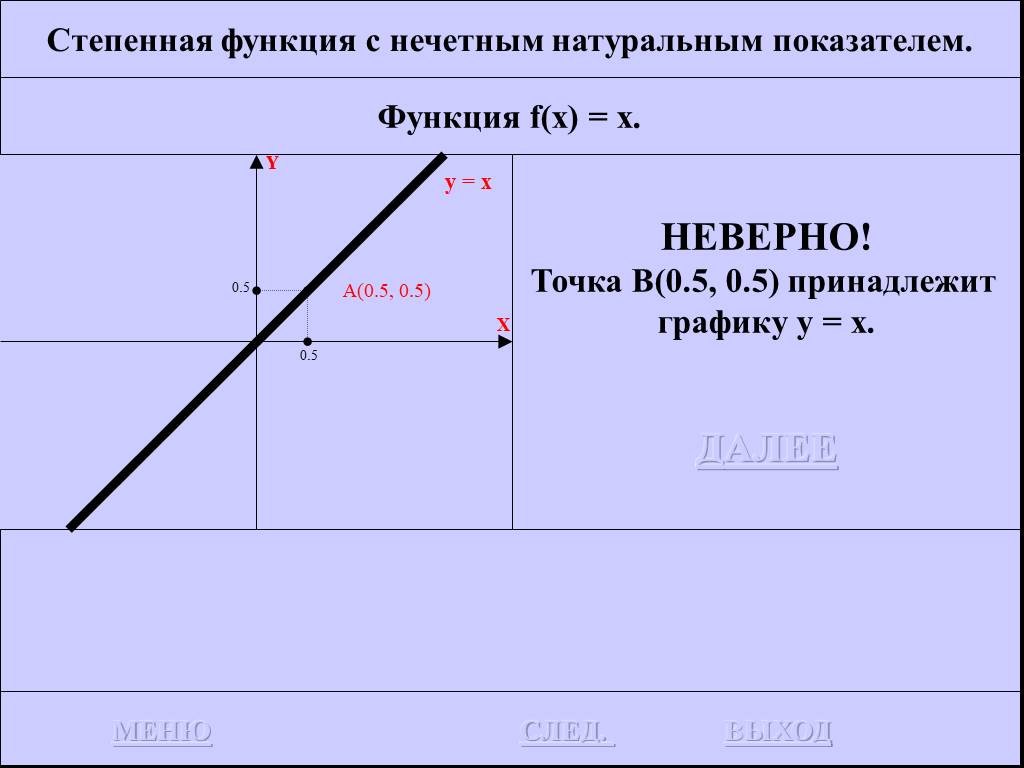
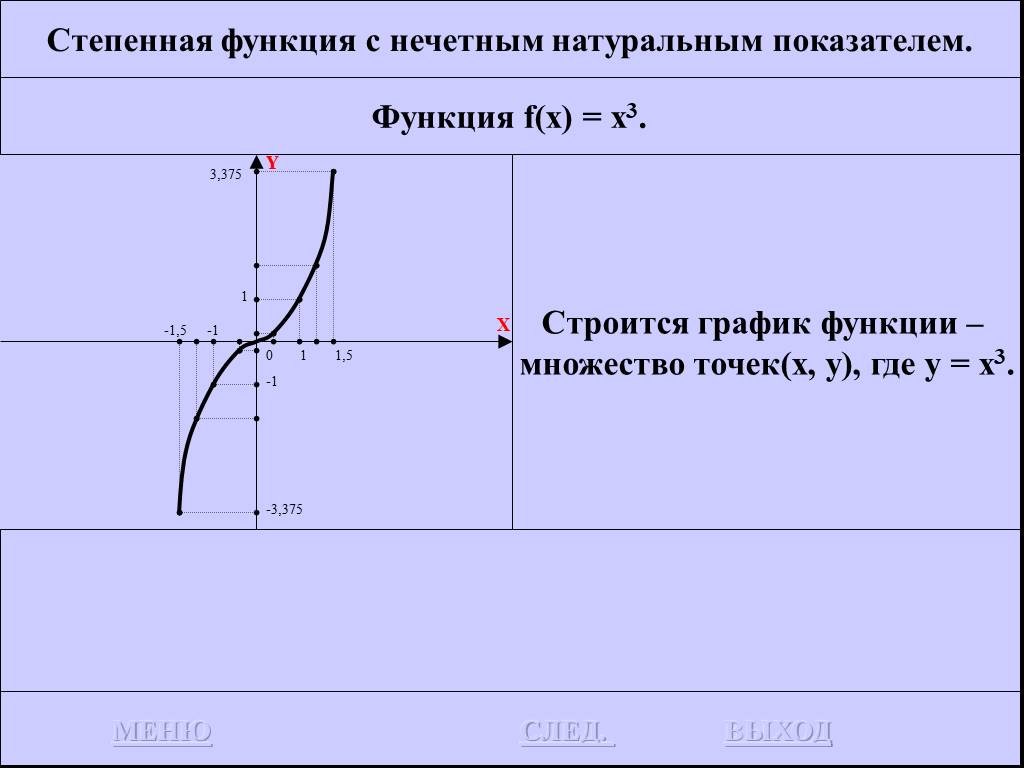
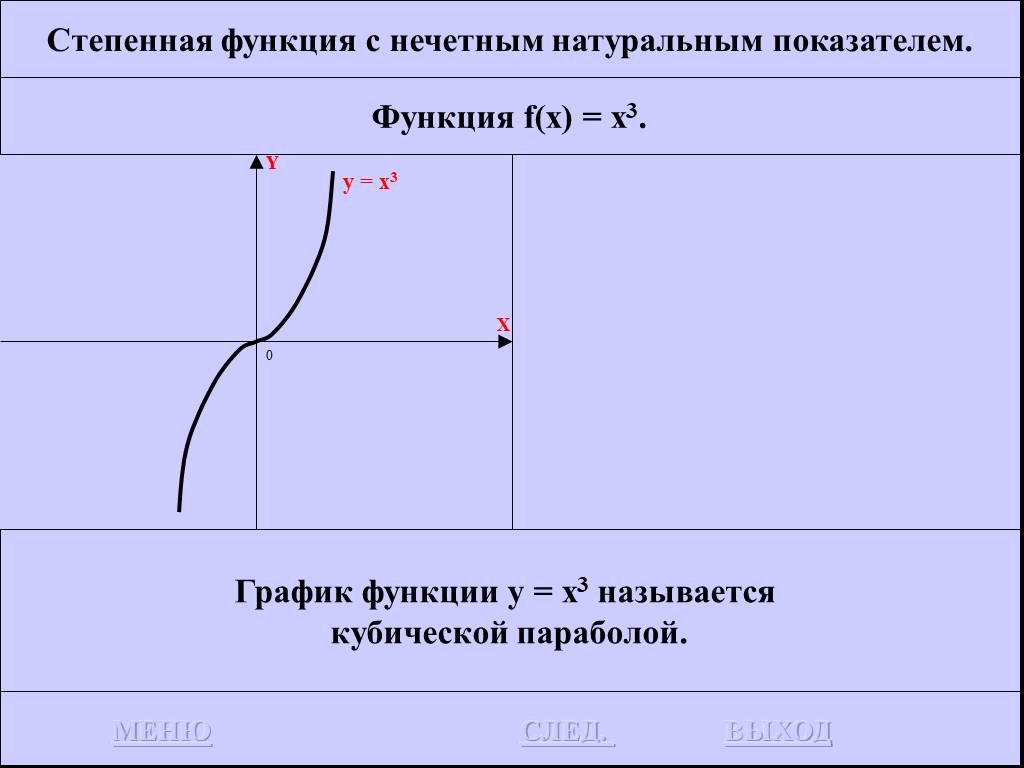
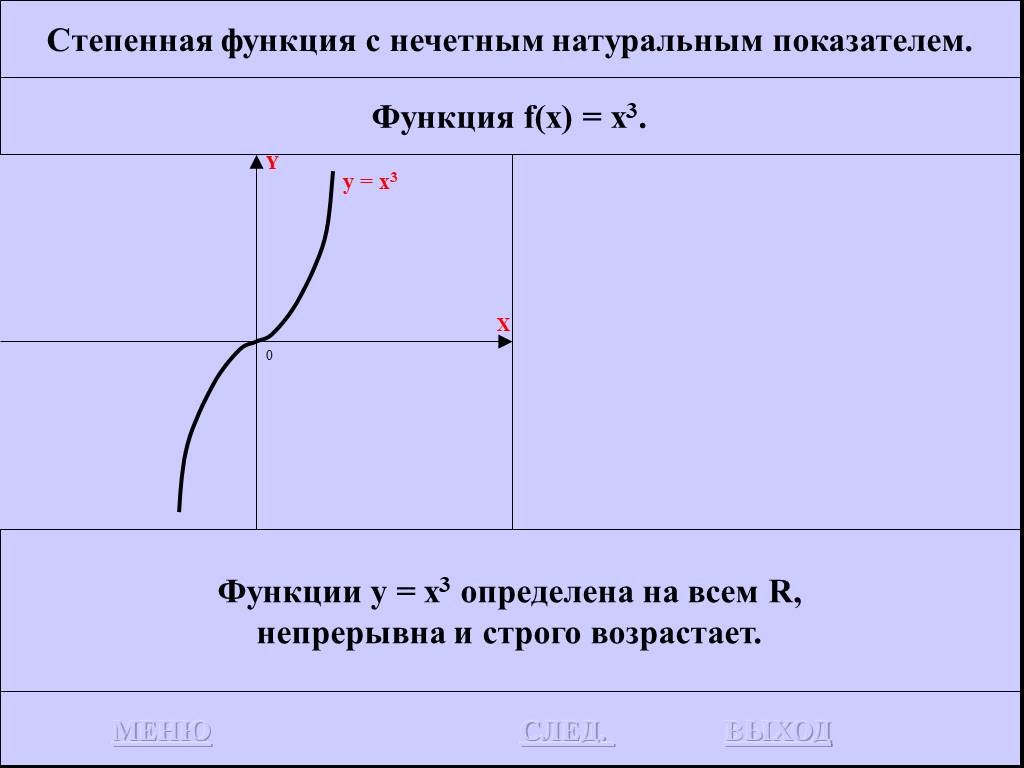
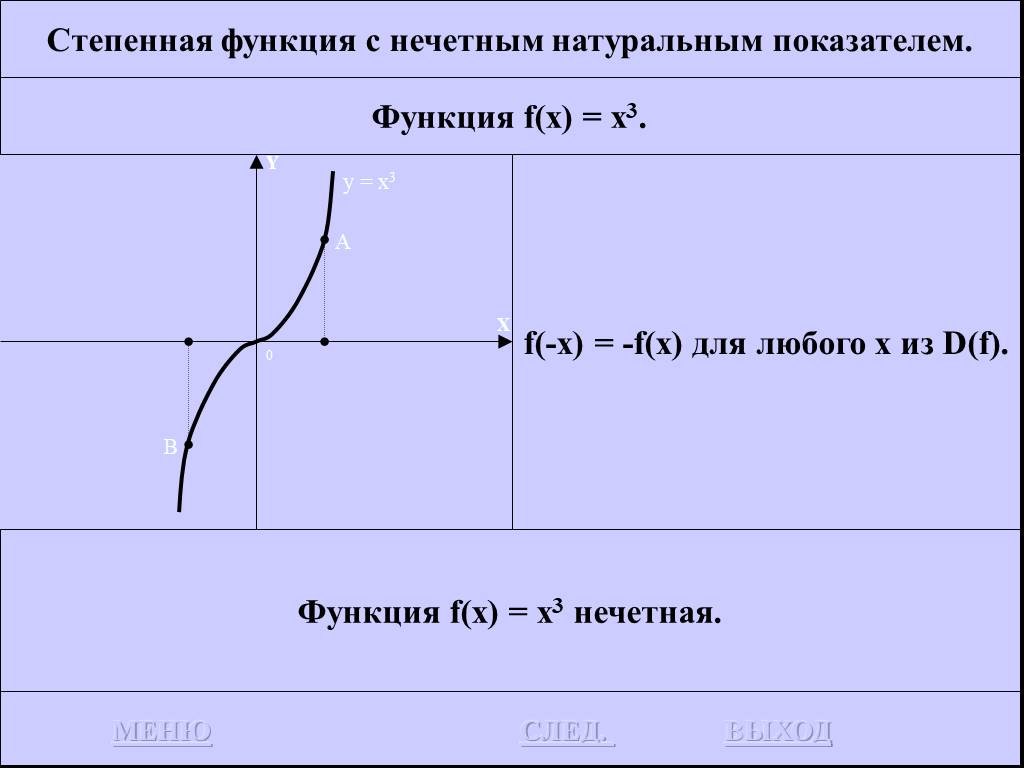
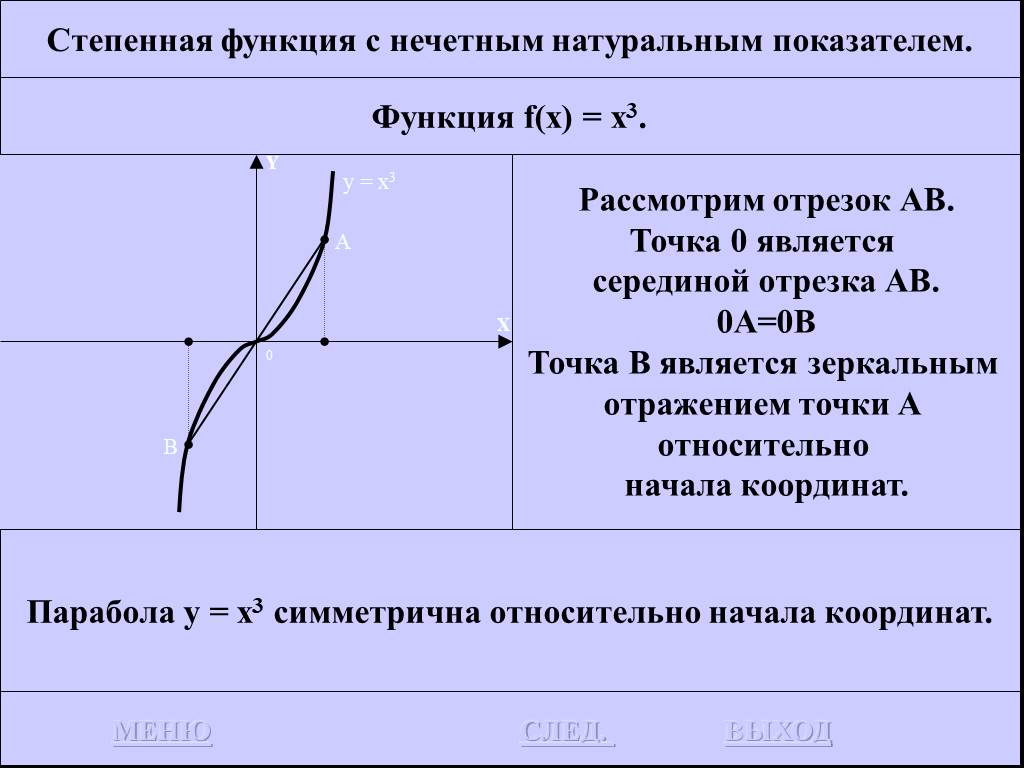
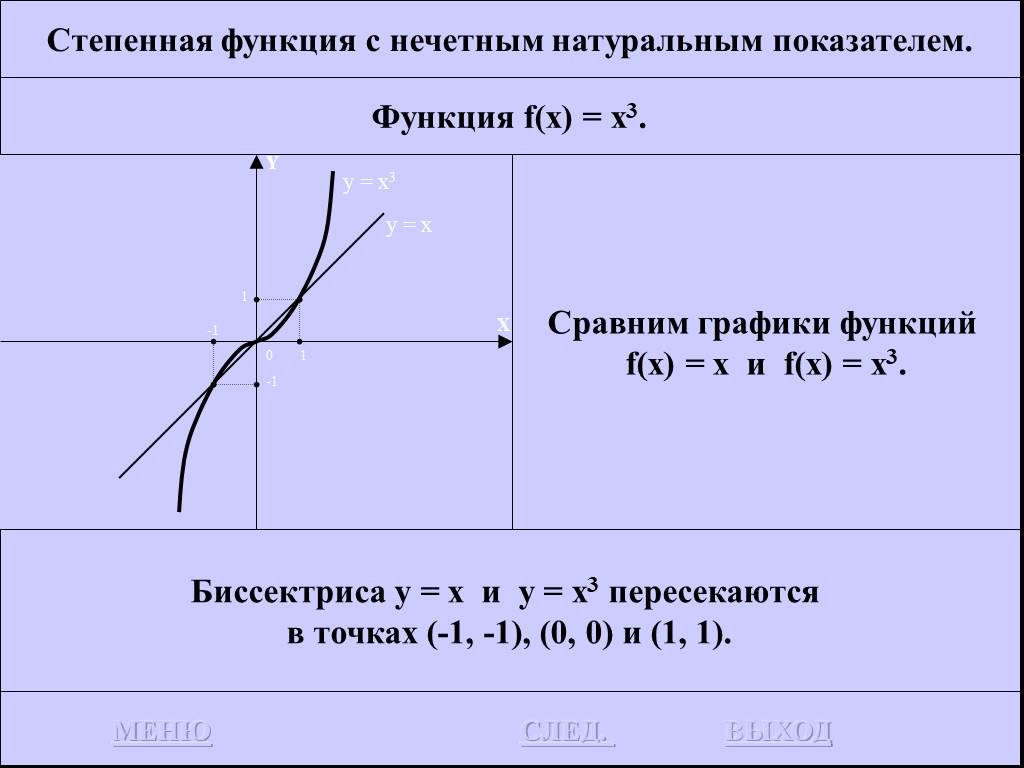
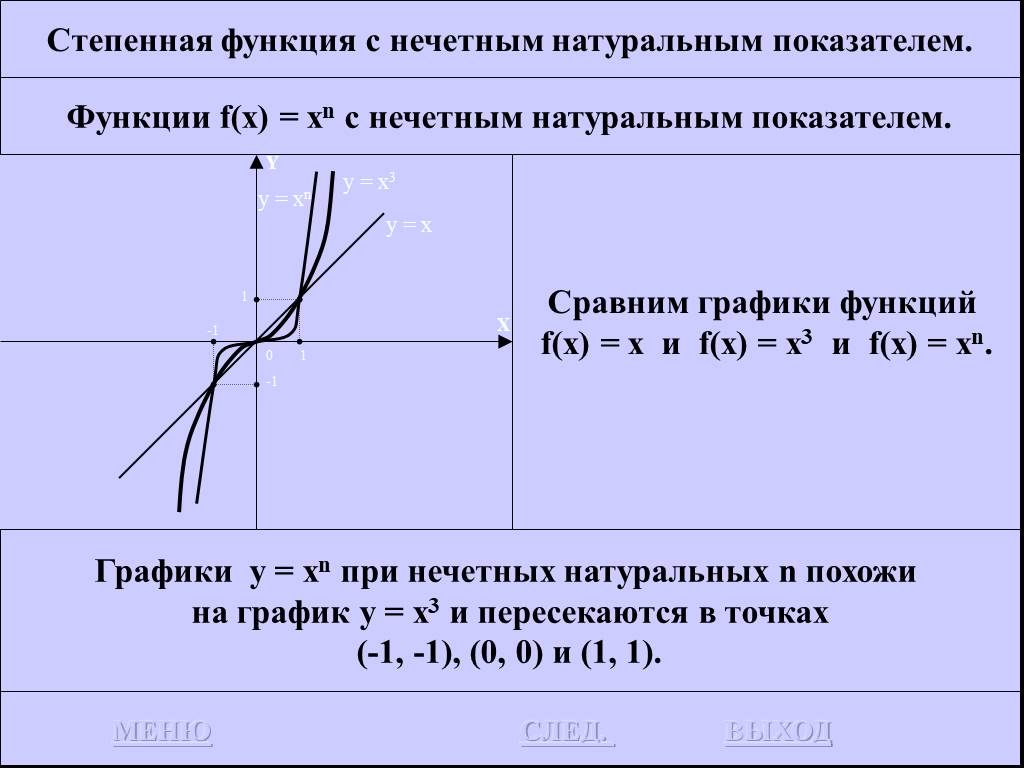

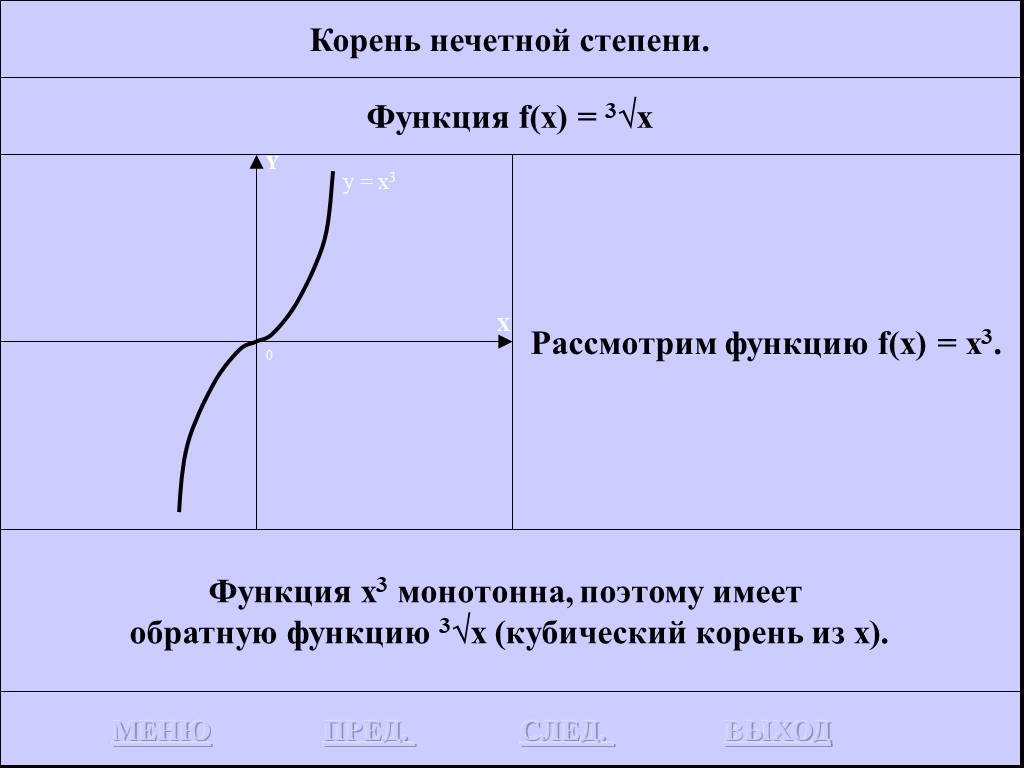
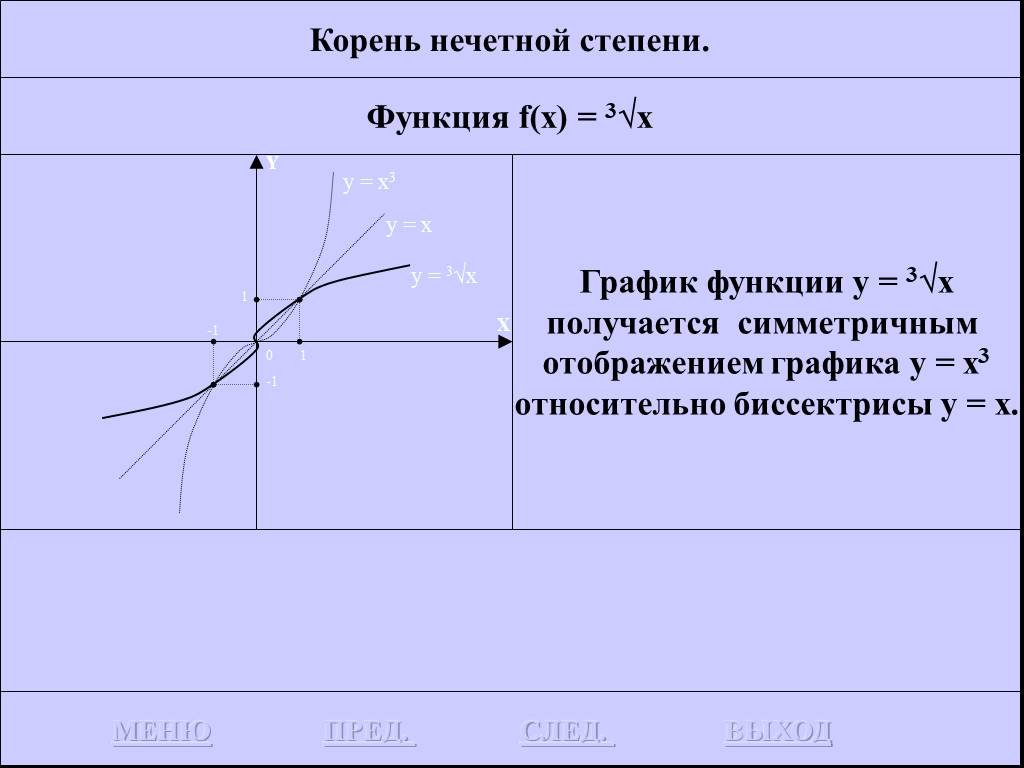
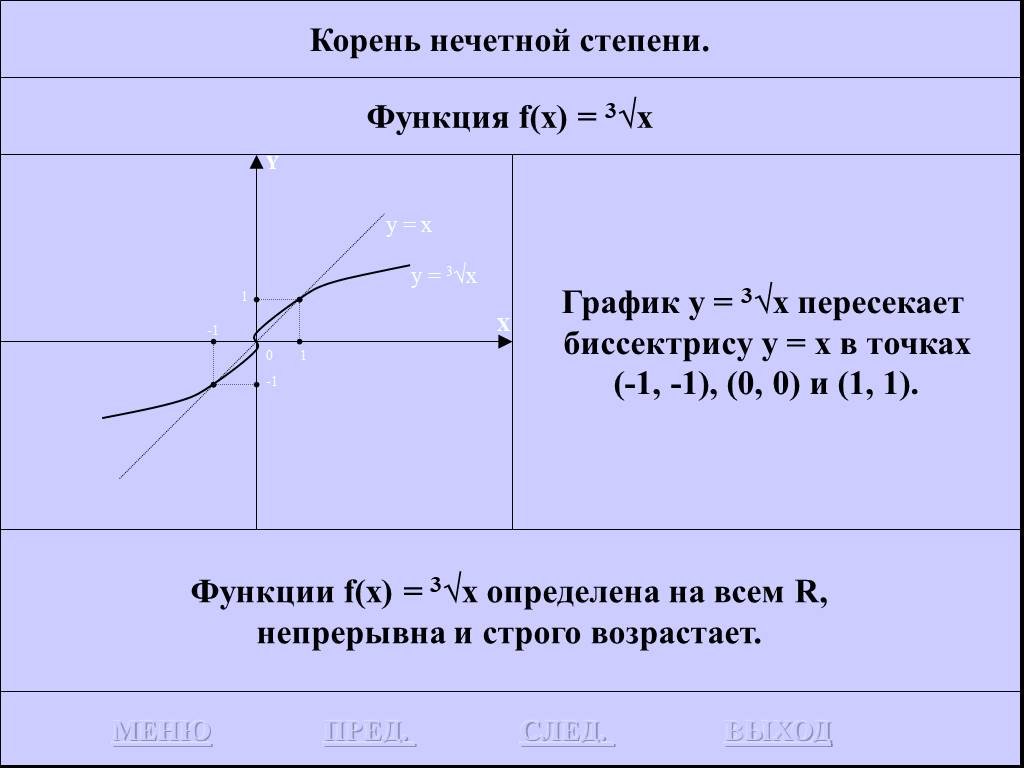
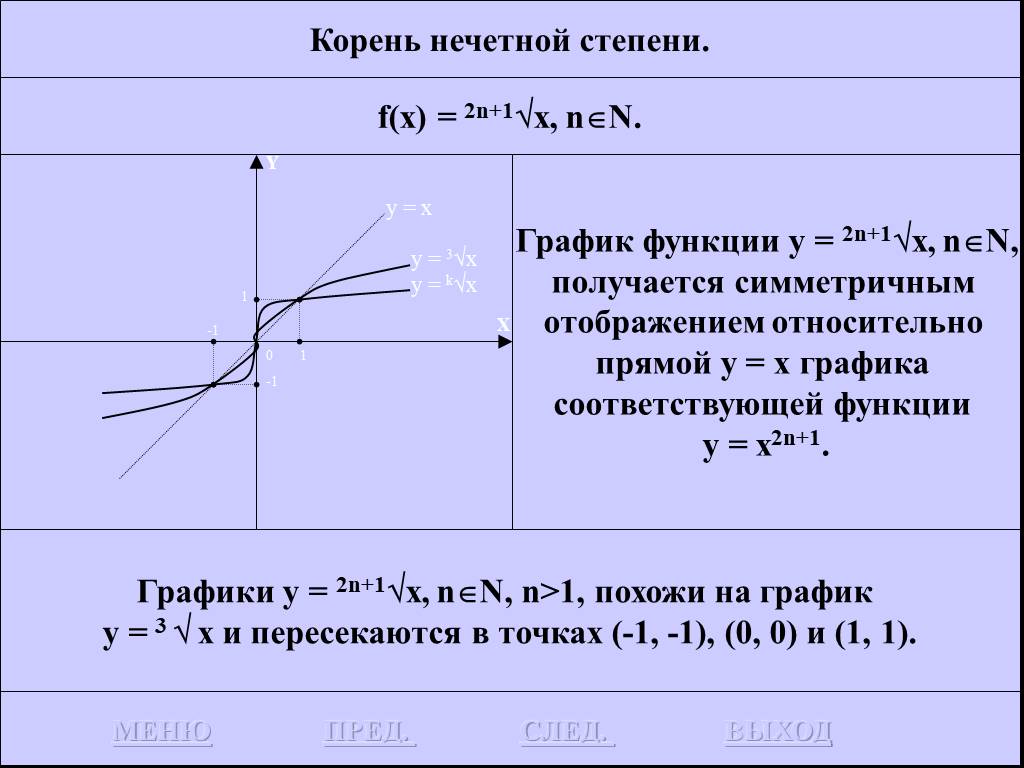
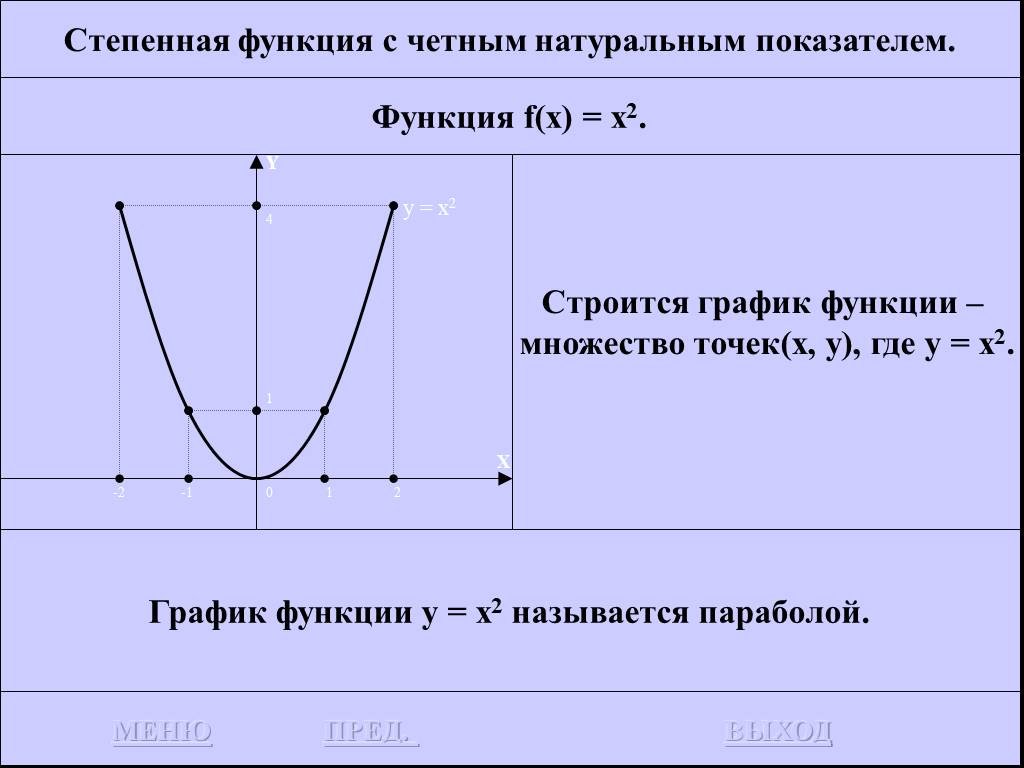
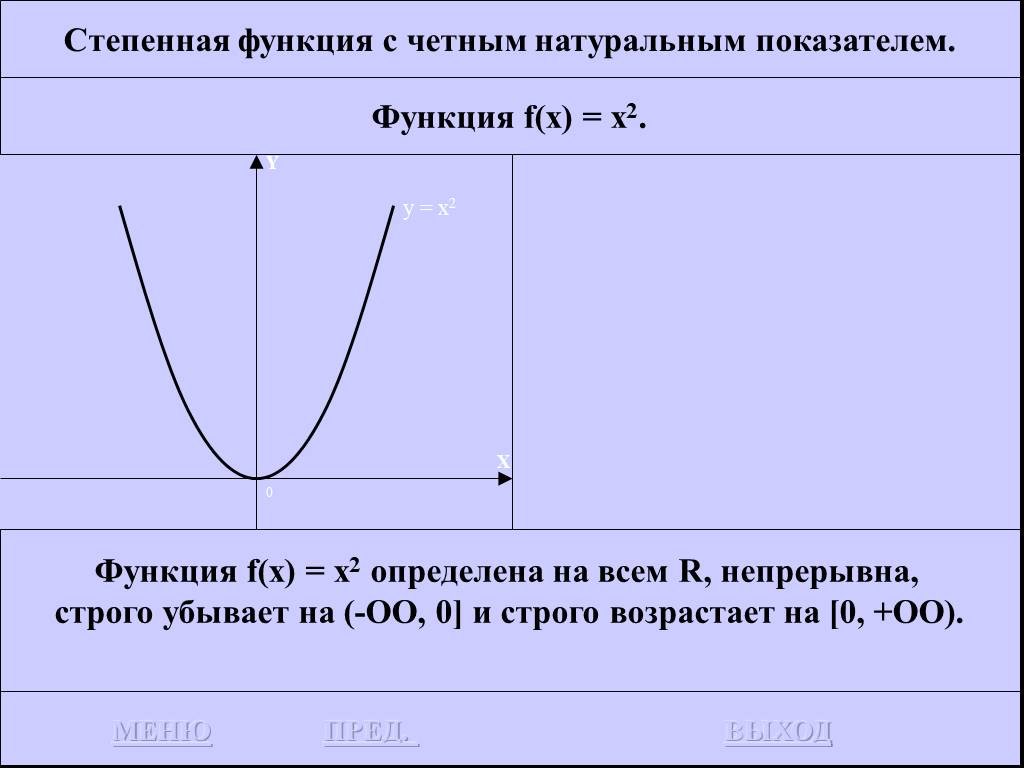
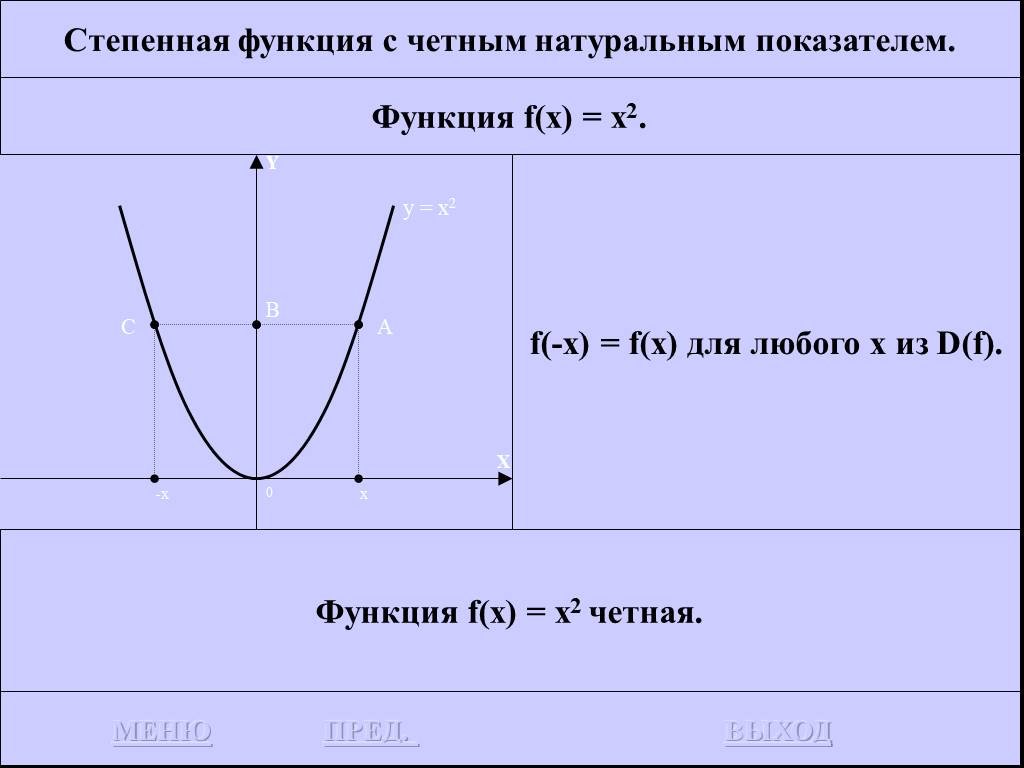
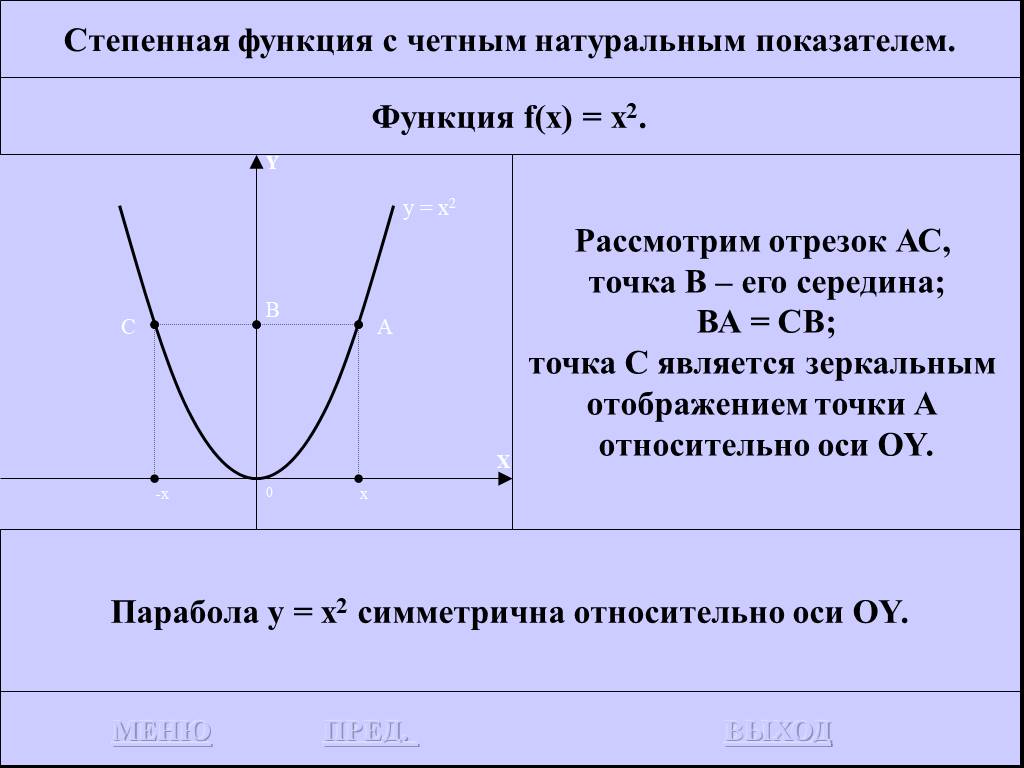
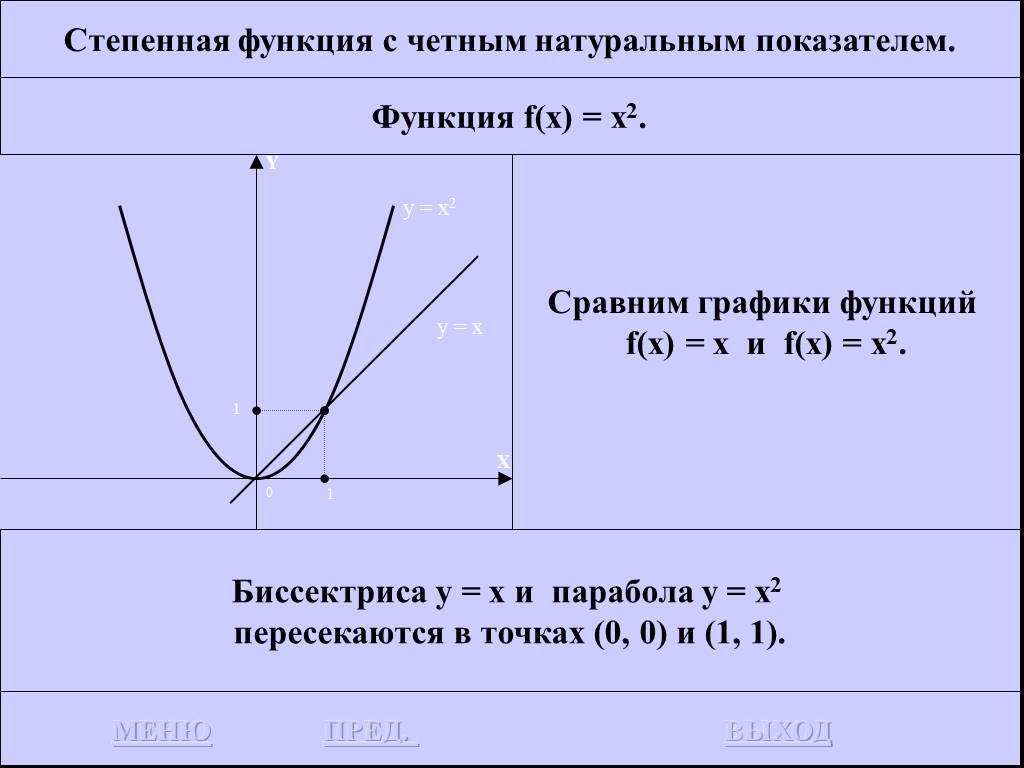
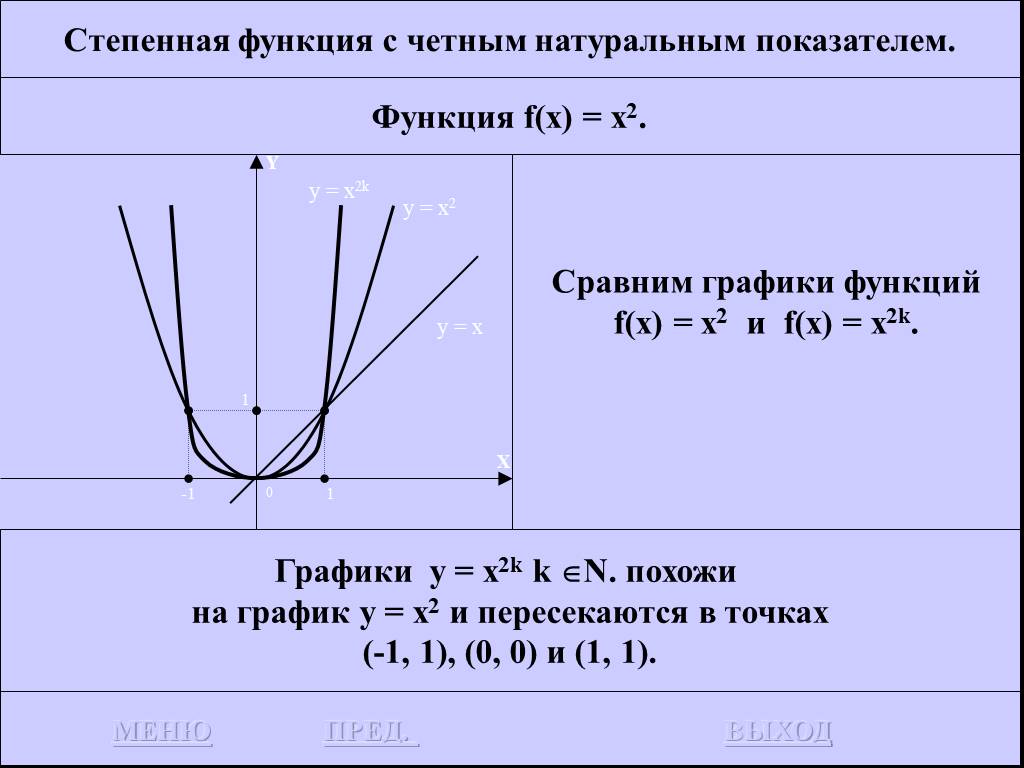




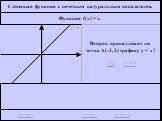
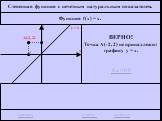
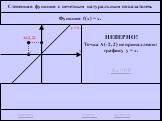
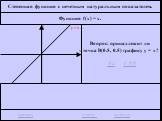

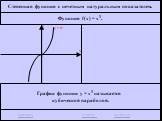
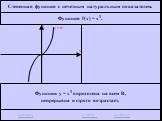


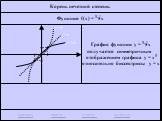
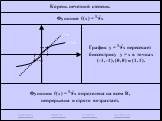
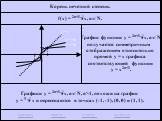
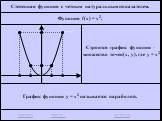
![Функция f(x) = x2 определена на всем R, непрерывна, строго убывает на (-OO, 0] и строго возрастает на [0, +OO). Функция f(x) = x2 определена на всем R, непрерывна, строго убывает на (-OO, 0] и строго возрастает на [0, +OO).](https://prezentacii.org/upload/cloud/19/01/116213/images/thumbs/screen26.jpg)