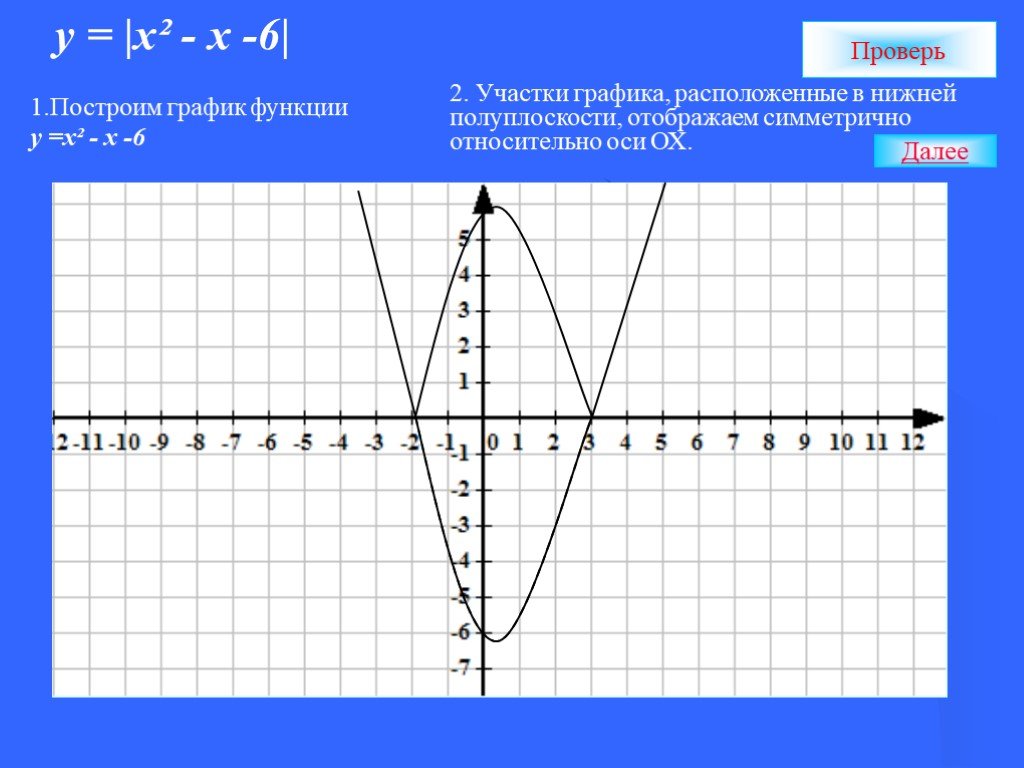
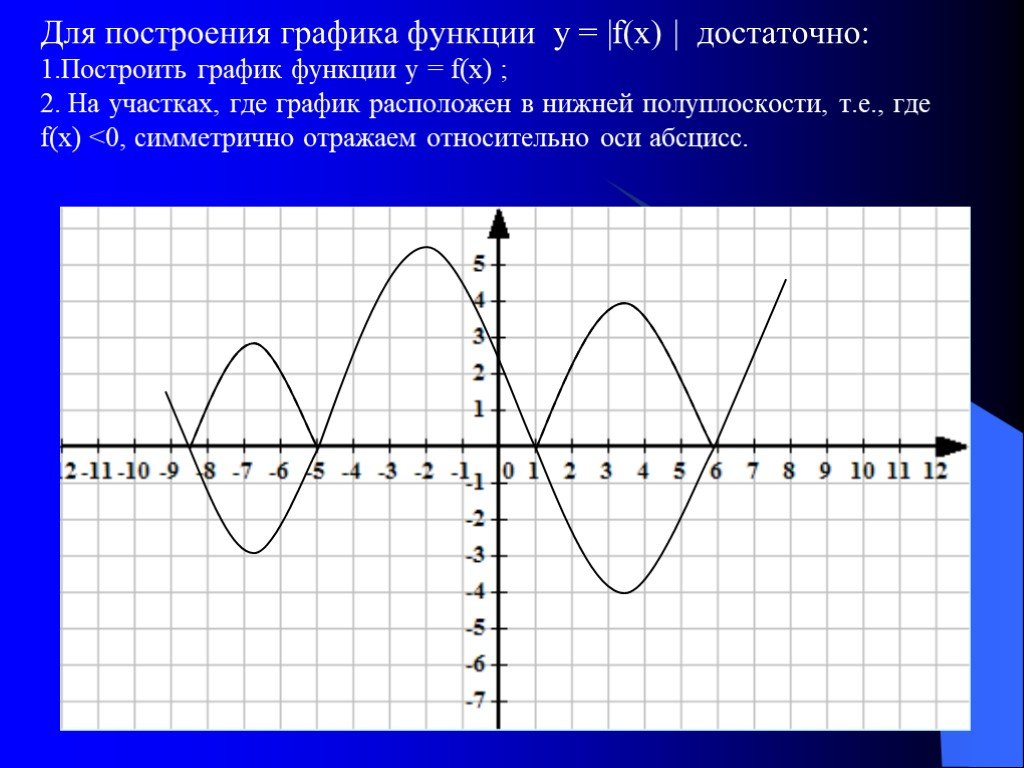
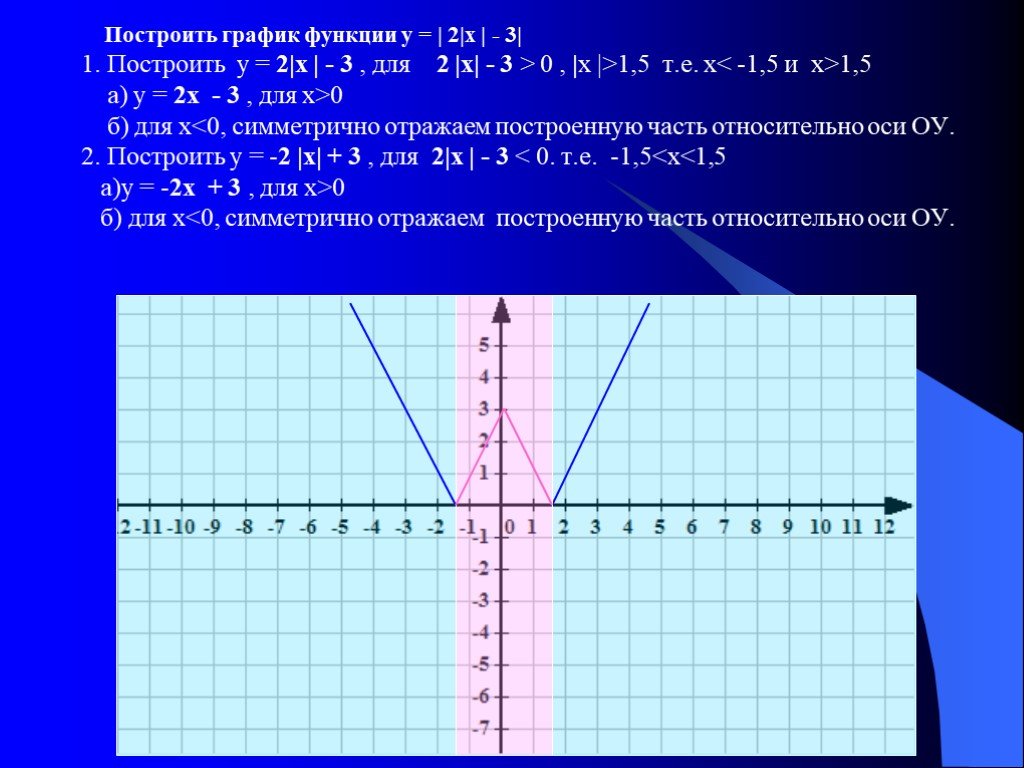
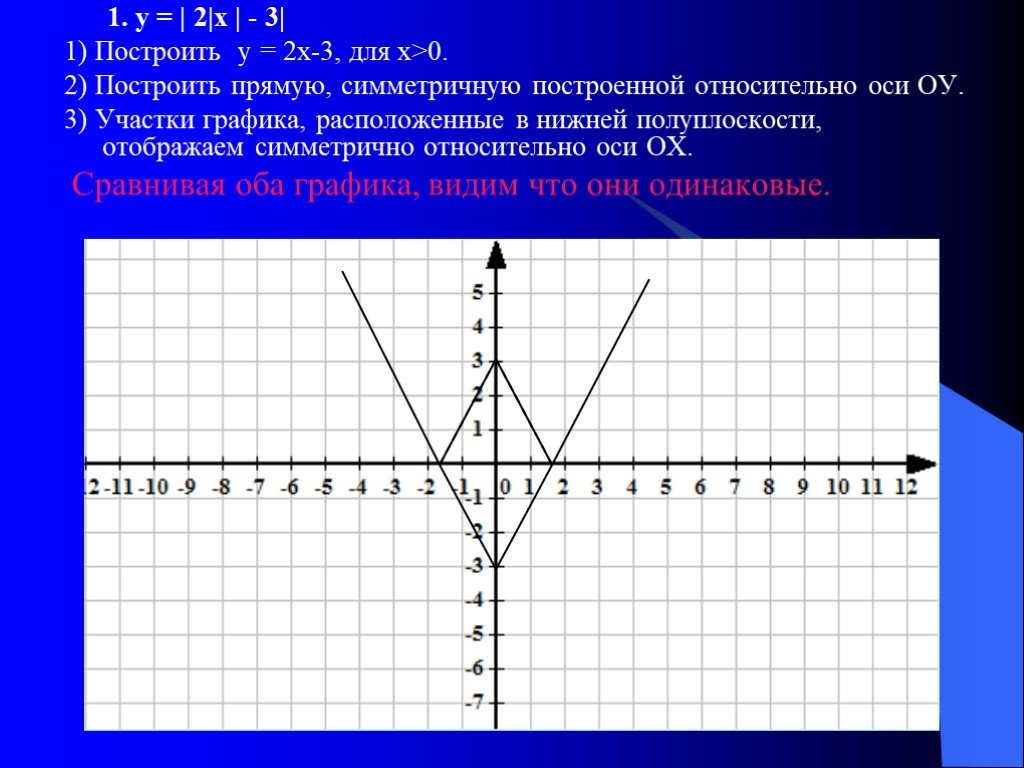
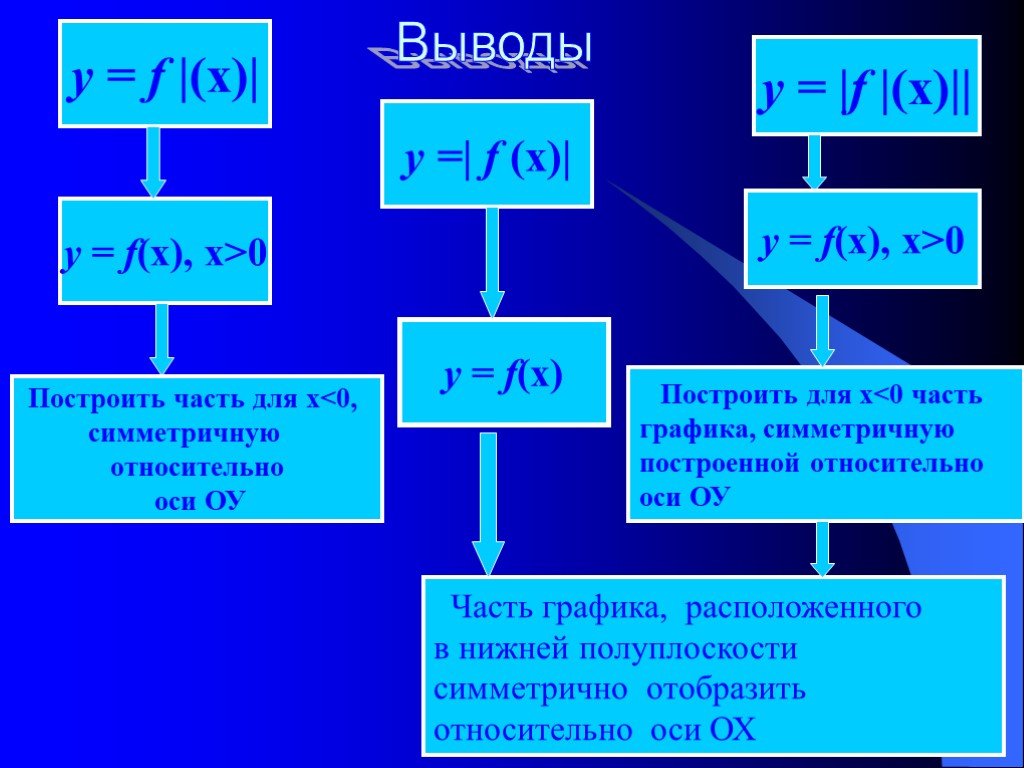
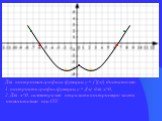
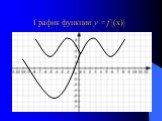
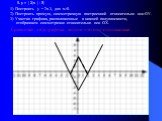
Презентация "Алгоритмы построения графиков функции" по математике – проект, доклад
Презентацию на тему "Алгоритмы построения графиков функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение различных задач с помощью построения графиков функции
ЦЕЛИ:. Рассмотреть аналитический и графический способы решений уравнений Выяснить, какой способ и при каких условиях является наиболее удобным для ...Зачем нужно строить асимптоты графиков дробно-рациональной функции?
В работе сделан экскурс в историю возникновения понятия асимптоты, сделан сравнительный анализ различных определений асимптоты. Рассматривается построение ...Преобразования графиков квадратичной функции
Квадратичной функцией называется функция вида у = ax²±bx±c Например : у=2x²+3x-4, а=2, b=3,c=-4 Графиком квадратичной функции является парабола Для ...Преобразование графиков функции
Повторение. Как построить график функции если известен график функции. . Рассмотрим построение графика функции. 1 случай: m – положительное число. ...Алгоритм построения графика квадратичной функции
1)направление «ветвей» параболы. если а>0, то «ветви» параболы направлены вверх; если а 0 - «ветви» параболы направлены вверх;. 2)Нахождение координат ...Взаимное расположение графиков линейной функции
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Алгоритмы - их функции и виды
Разветвляющийся алгоритм. Сюда пойдешь – клад найдешь. Сюда пойдешь – жену найдешь. Сюда пойдешь – мегабайт найдешь. Составить блок-схему алгоритма ...Производная функции
Проблемный вопрос. Можно ли находить производные, не используя определение? Существуют ли более удобные способы? Цели и задачи. Научиться находить ...Преобразование графиков тригонометрических функций
y = cos(x+2) y=cos2x y=sinx +2 y=-3cosx y=sin1/2x y=sin(x-5) y=tg2x y=2ctgx y=ctg1/3x y=1/3sinx y=4-cosx y=ctgx+1. Сгруппируйте функции по какому-нибудь ...Построить график функции
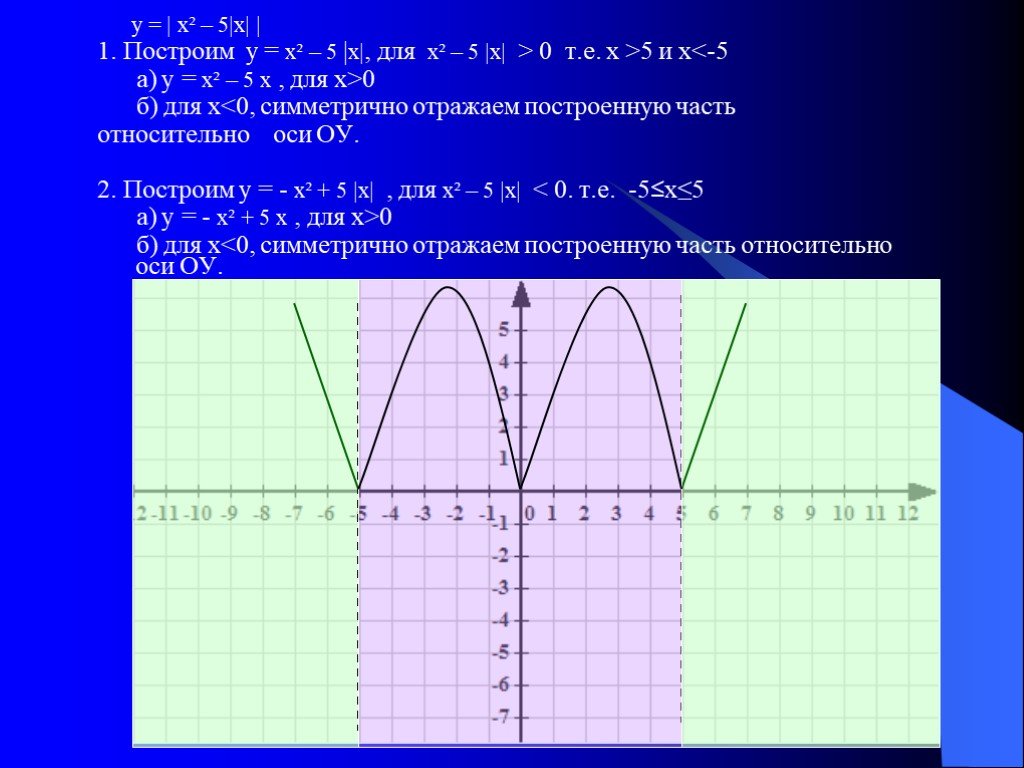
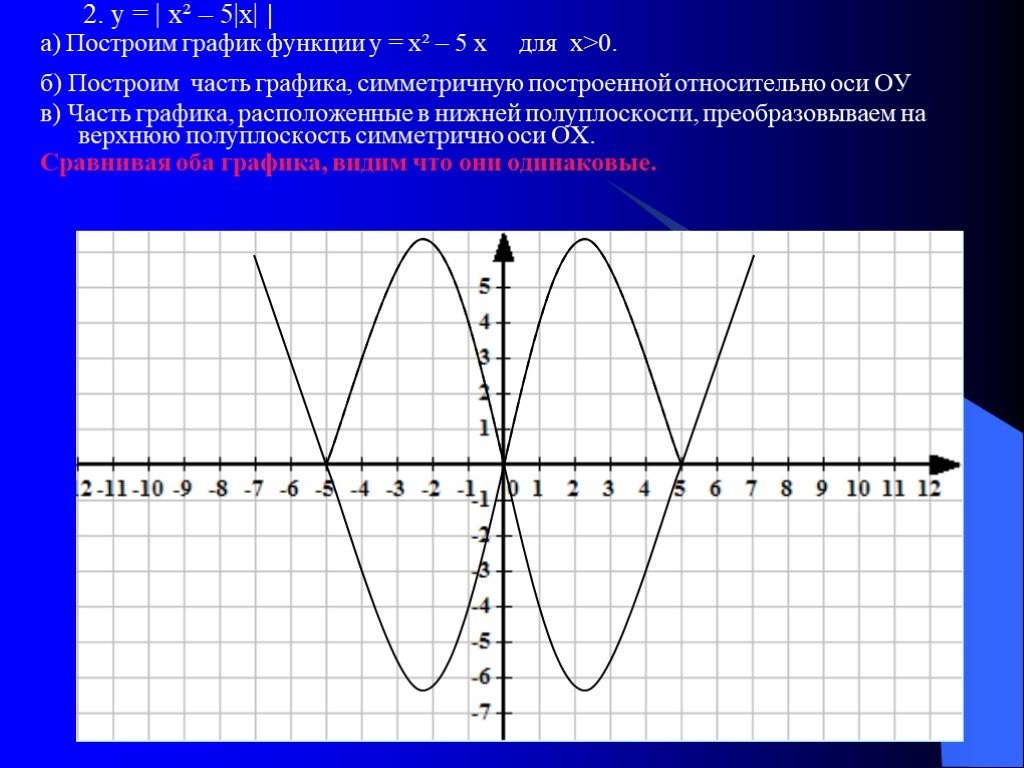
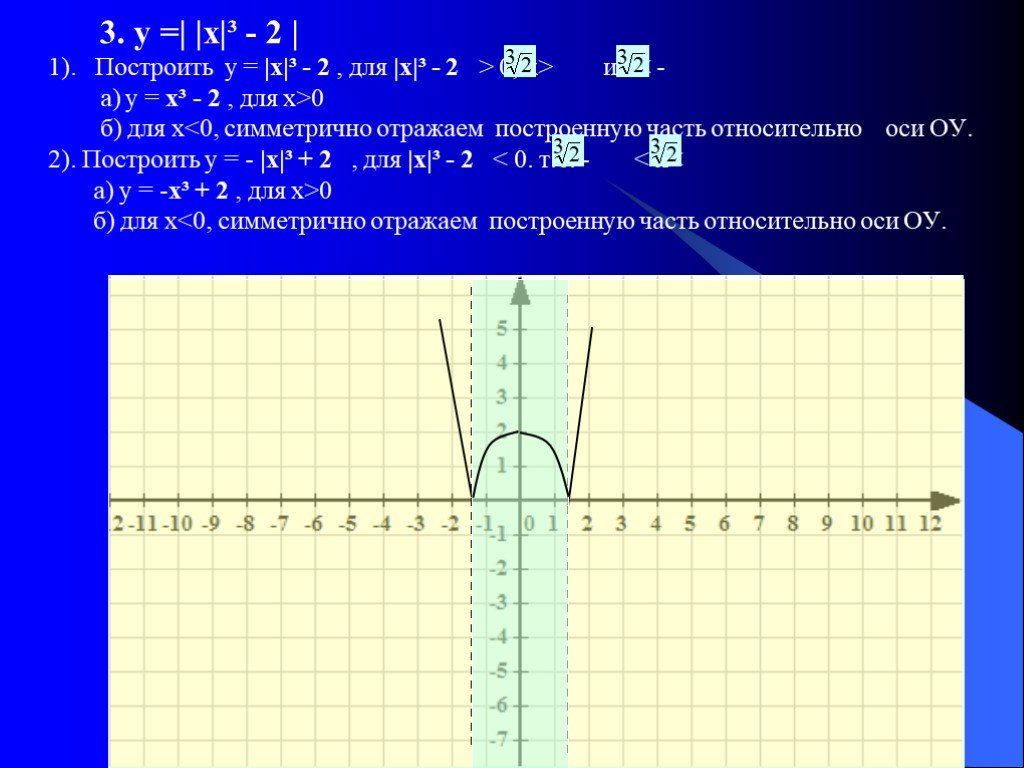
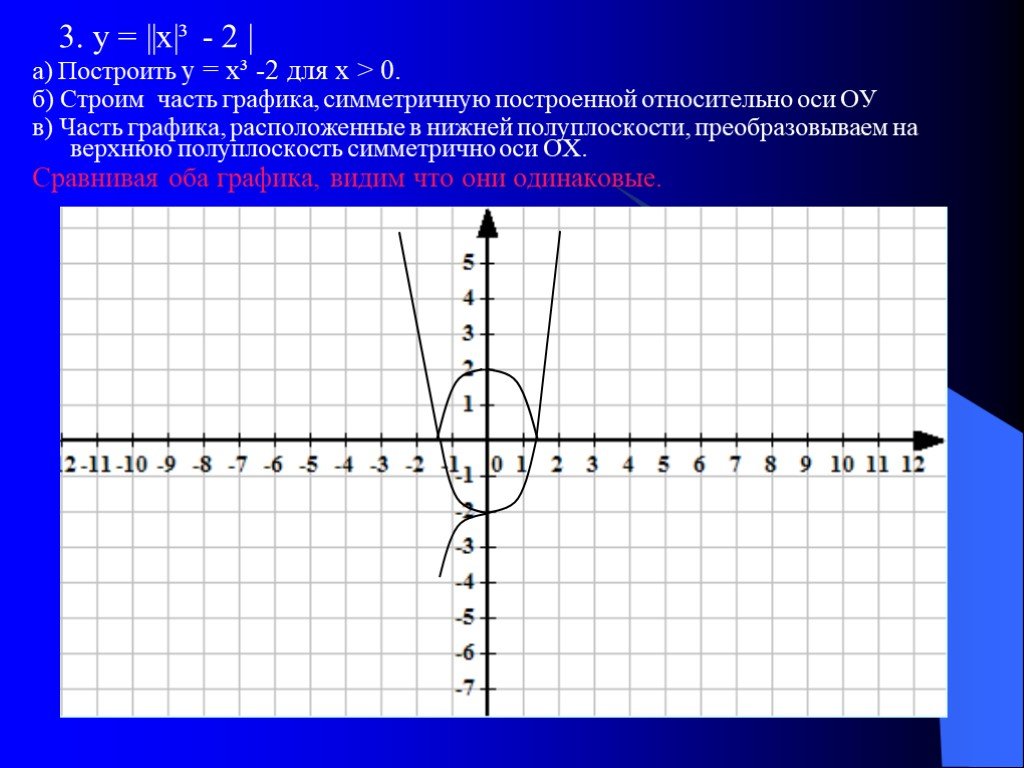
Содержание:. 1. Функция y=sin x, её свойства и разновидности; 2. Функция y=cos x, её свойства и разновидности; 3. Примеры задач. 4. Закончить просмотр. ...Построение графиков функций и уравнений, содержащих переменную под знаком модуля
Тема урока: «Построение графиков функций и уравнений, содержащих переменную под знаком модуля». Тип урока:. «Урок обобщения и систематизации знаний». ...Понятие функции
Множество х: Все Жильцы.Множество y: номера квартир.
Правило соответствия (зависимости) между множествами : «Каждому жильцу дома будет соответствовать ...
Сопряжение. Геометрические построения
Дать понятие о сопряжении, об элементах, обязательных в любом сопряжении. Ознакомить с правилами построения сопряжения двух прямых и с правилами построения ...Взаимно обратные функции
Цель проекта: Изучить поведение взаимно обратных функций. Установить связь графиков прямой и обратной функций. Подготовиться к успешной сдаче ЕГЭ. ...Асимптоты. Построение эскизов графиков
Определение: прямая вида x=a называется вертикальной асимптотой для y=f(x), если. 1. Определение: прямая вида y=b называется горизонтальной асимптотой, ...Алгоритмы теории игр
План лекции. Введение Матричные игры Игры с седловой точкой Смешанные стратегии Применение Итоги Литература. Введение. Первая значительная книга по ...Алгоритмы с ветвлениями
Найди ошибку. Вставить ключ в замочную скважину. Достать ключ из кармана. 3. Вынуть ключ. 4. Повернуть ключ два раза против часовой стрелки. Найди ...Алгоритмы работы с величинами
Цель:. Познакомиться с понятием «величина» и показать ее назначение в программировании. 1. Как называется алгоритм, записанный на «понятном» компьютеру ...Алгоритмы работы на координатной плоскости
Цели:. Формировать умение работать на координатной плоскости как с положительными, так и отрицательными координатами. Развивать алгоритмическое мышление. ...Алгоритмы внутренних точек с приближенным решением вспомогательной задачи
1939 – линейное программирование (Канторович). 1947 – симплекс-метод (Данциг). 1967 – метод внутренних точек (Дикин). 1984 – полиномиальный МВТ (Кармаркар). ...Конспекты
Взаимное расположение графиков линейной функции
Открытый урок по алгебре в 7 классе на тему: «Взаимное расположение графиков линейной функции». Напомните пожалуйста, что мы изучали на прошлом ...Преобразование графиков тригонометрических функций
Тема урока : "Преобразование графиков тригонометрических функций ". . . Цели: . . -. образовательные:. обобщить и систематизировать знания ...Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения
Предмет:. алгебра 10 кл. Тема урока:. «Преобразование графика тригонометрической функции у = sin. x. путем сжатия и расширения». Тип урока:. ...Построение графика квадратичной функции, содержащей модуль
Урок по алгебре для 9 класса по теме:. «Построение графика квадратичной функции, содержащей модуль». Конспект урока. Автор:. учитель математики. ...Чётность и нечётность функций. Нулевые функции
АЛГЕБРА И НАЧАЛА АНАЛИЗА. Тема урока. «Чётность и нечётность функций. Нулевые функции». Цели урока. . . Образовательные:. повторить основные ...Степенные функции, их свойства и графики
Конспект урока на тему. «Степенные функции, их свойства и графики». Учитель. : Чижова Светлана Анатольевна г. Иваново. Тип урока:. урок формирования ...Решение квадратных неравенств с помощью графика квадратичной функции
План конспект урока. Тема:. « Решение квадратных неравенств с помощью графика квадратичной функции». Ф.И.О. Квашнина Мария Андреевна. Место работы: ...Производная показательной и логарифмической функции
КГУ «Средняя школа №7 города Зыряновска». «Производная показательной и логарифмической функции». Учитель: ...Взаимное расположение графиков линейных функций
Тема:. Взаимное расположение графиков линейных функций. Тип урока. : Совершенствование знаний, умений, и навыков. Цели урока:. Выяснить ...Взаимное расположение графиков линейных функций
Тема урока: « Взаимное расположение графиков линейных функций». Цель урока:. закрепить умения и навыки нахождения углового коэффициента, познакомить ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию