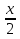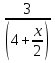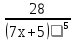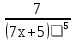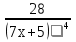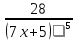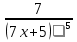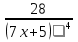Конспект урока «Производная сложной функции» по математике

Открытый урок
по теме: «Производная сложной функции»
Тип урока: комбинированный
Цели:
образовательная:
- формирование умения находить по правилу производную сложной функции;
- отработка алгоритма применения правила нахождения производной сложной функции при решении примеров.
развивающая:
- развивать умение обобщать, систематизировать на основе сравнения, делать вывод;
- развивать наглядно-действенное творческое воображение;
- развивать познавательный интерес.
воспитательная:
- воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов при нахождении производных сложных функций;
- формирование умения рационально, аккуратно оформить задание на доске и в тетради.
- воспитание дружеского отношения при проведении урока.
Ученик должен знать:
понятие сложной функции, правило нахождения ее производной.
Ученик должен уметь:
находить по правилу производную сложной функции, использовать это правило при решении примеров.
Межпредметные связи: физика, геометрия, экономика.
Оснащение урока: мультимедиа-проектор, магнитная доска, классная доска, мел, раздаточный материал к уроку.
План урока:
1. Сообщение цели, задач урока и мотивации учебной деятельности – 2 мин.
-
Проверка выполнения домашнего задания – 3 мин (фронтальная проверка, самоконтроль).
-
Устный счет – 5 мин (фронтальная работа, взаимоконтроль).
-
Подготовка к усвоению (изучению) нового учебного материала через повторение и актуализацию опорных знаний – 5 мин (проблемная ситуация).
-
Изучение нового материала – 13 мин (фронтальная работа под руководством преподавателя).
-
Первичное осмысление и понимание нового материала - 10 мин (фронтальная работа: один учащийся показывает решение примера на доске, остальные решают в тетрадях).
-
Закрепление новых знаний – 10 мин (самостоятельная работа – тест в двух вариантах, с дифференцированными заданиями).
-
Информация о домашнем задании, инструкция о его выполнении – 2 мин.
-
Подведение итогов урока, рефлексия – 2 мин.
I. Ход урока: Сообщение цели, задач и плана урока, мотивации учебной деятельности:
- проверить подготовленность аудитории и готовность учащихся к уроку, отметить отсутствующих.
- отметить, что на данном уроке продолжается работа по теме “Производная функции”.
II. Проверка домашнего задания.
На дом заданы примеры №221,223,226,227(в,г):
- учащиеся индивидуально проверяют свои ответы и ставят себе (самоконтроль) оценку в лист контроля. У каждого ученика имеется лист контроля, критерий оценки за домашнюю работу и образец листа контроля в раздаточном материале к уроку
Лист контроля
| Домашняя работа | Тест | Итоговая оценка | |
|
|
|
|
|
- вызвать к доске ученика показать оформление решения примера № 227 с комментарием выполненных действий.
- обратить внимание на правильное решение и правильное оформление решения домашнего примера
III. Устный счет.
-
Задайте формулами элементарные функции, из которых составлена сложная функция: f(x)=sin(x2+3); g(x)=
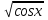 ; h(x)=
; h(x)=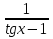 ;
; -
Найдите область определения функций:
F(x)=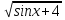 ; g(x)=
; g(x)=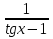
IV. Подготовка к (усвоению) изучению нового учебного материала через повторение и актуализацию опорных знаний.
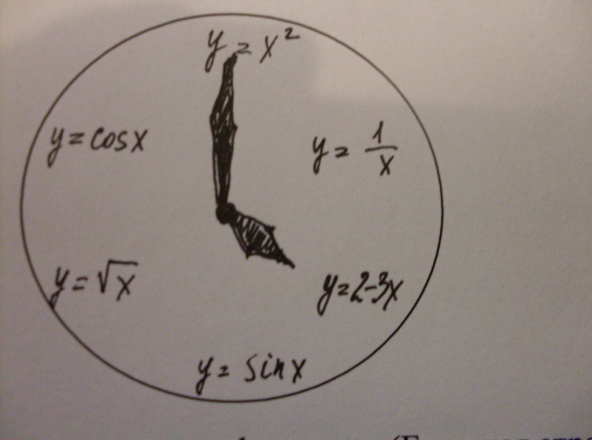
Cоставьте сложную функцию (Большая стрелка – «главная» функция, маленькая стрелка – «подчиненная» функция)
- постановка проблемно ситуации: найти производную функции y=(2x+3)100; y=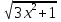
- на прошлых уроках мы научились находить производные элементарных функций. Функции y=(2x+3)100; y=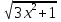 сложные. Умеем ли мы находить производные сложных функций?
сложные. Умеем ли мы находить производные сложных функций?
[Нет.]
Значит, с чем мы должны сегодня познакомиться?
[С нахождением производной сложных функций.]
Учащиеся сами формулируют тему и задачи урока, преподаватель записывает тему на доске, а ученики – в тетради.
- историческая справка, связь с будущей профессиональной деятельностью.
V. Усвоение новых знаний.
- показать на доске нахождение производных функций y=(2x+3)100; y=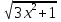 ;
;
- объяснение построить на основе изложенного материала в учебном пособии ( стр 119).
VI. Первичное осмысление и понимание нового материала.
- повторить алгоритм нахождения производной сложной функции;
- решить примеры: № 224(а,б), №225(а,б), №230(а,б)
Дополнительные задания
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
VII. Закрепление новых знаний с помощью теста по вариантам.
Задания с тестами дифференцированные: примеры с № 1-3 оцениваются на “3”, до № 4 – на “4”, все пять примеров – на “5”.
Ученики решают в тетради и проверяют ответы друг у друга с помощью мультимедиа и ставят оценку друг другу (взаимоконтроль) в лист контроля.
Тест.
Вариант 1.
Найти производные функций. (А., В., С. – ответы)
| Задание | Ответы | |||
| А | В | С | ||
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 | y =(4+ |
|
|
|
| 5 |
|
|
|
|
Вариант 2.
Найти производные функций. (А., В., С. – ответы)
| Задание | Ответы | |||
| А | В | С | ||
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 | Y=(7x+5)-4 | |
|
|
| 5 |
|
|
|
|
VIII. Информация о домашнем задании, инструкция о его выполнении.
Домашнее задание: п. 16(2) №224(в,г), №225(в,г), №230(в,г)
IX. Подведение итогов урока, рефлексия:
- сдача листов контроля;
- рефлексия.
| Домашняя работа | Тест | Итоговая оценка | |
|
|
|
|
|
ТЕСТ Вариант 1. Найти производные функций. (А., В., С. – ответы)
| Задание | Ответы | |||
| А | В | С | ||
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 | y =(4+ |
|
|
|
| 5 |
|
|
|
|
| Домашняя работа | Тест | Итоговая оценка | |
|
|
|
|
|
ТЕСТ. Вариант 2. Найти производные функций. (А., В., С. – ответы)
| Задание | Ответы | |||
| А | В | С | ||
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 | Y=(7x+5)-4 | |
|
|
| 5 |
|
|
|
|
Здесь представлен конспект к уроку на тему «Производная сложной функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.