Конспект урока «Производная» по математике для 10 класса
Зачётный урок по теме: «Производная».
10 класс
Цели.
-
Контроль знаний, умений, навыков по теме: «Производная».
-
Подготовка учащихся к итоговой аттестации.
3. Формирование грамотной математической речи, умения слушать
своих одноклассников, анализировать и оценивать их ответ.
4. Формирование трудовых навыков, умения распределять своё
рабочее время на уроке, приобщение к самостоятельному труду.
5. Формирование математического мировоззрения
6. Формирование умения обсуждать и корректировать ответы своих
одноклассников, дополнять их.
7. Формирование интереса к предмету математики путём
использования нестандартных форм и приёмов, игровых
моментов, использование ИКТ.
8. Формирование математической культуры: культуры речи, аккуратного и
грамотного оформления записей в карточке и в тетради , использование
математических терминов и символики.
Ход урока.
1 этап. Вводная часть. (2 мин.)
2 этап. Зачёт по теории. (10 мин.)
Учащиеся сидят в группах по 2-3 человека В каждую группу учитель направляет проверяющего (лучшие учащиеся класса, которые предварительно сдали учителю теоретический блок или освобождены от сдачи в результате своей отличной работы в процессе изучения данной темы), который задаёт вопросы из общего перечня каждому ученику группы. В результате каждый учащийся должны получить не менее 5 вопросов и ответить на них. В результате он зарабатывает соответствующую оценку за теоретический блок в индивидуальной карте ответов.
Задания теоретической части.
| | ||||
| № задания | Вопросы | Отметка проверяющего о правильности выполнения задания | ||
| 1 | Дать определение функции непрерывной в точке и на промежутке. | | ||
| 2 | Что такое приращение функции и приращение аргумента? | | ||
| 3 | Дать определение производной функции. | | ||
| 4 | Физический и геометрический смысл производной? | | ||
| 5 | Расскажите алгоритм отыскания производной. | | ||
| 6 | Какие основные формулы дифференцирования вам известны? | | ||
| 7 | Перечислите основные правила дифференцирования функции. Примеры. | | ||
| 8 | Расскажите алгоритм отыскания производной сложной функции. Примеры. | | ||
| 9 | Расскажите алгоритм составления уравнения касательной к графику функции у=f(х). | | ||
| 10 | Признаки монотонности функции. Примеры. | | ||
| 11 | Экстремумы функции(определения, признаки). | | ||
| 12 | Расскажите алгоритм исследования функции на монотонность и экстремумы. Примеры. | | ||
| 13 | Расскажите алгоритм исследования функции для построения графика. | | ||
| 14 | Расскажите алгоритм отыскания наибольшего и наименьшего значений функции на промежутке. | | ||
| 15 | Применение производной в жизни. Примеры. | | ||
| Оценка учителя за практическую часть | | Оценка проверяющего | | |
Теоретический зачёт сопровождается слайдами на интерактивной доске, где отражены вопросы и критерий оценивания.
|
|
3 этап. Зачёт по практике. ( 25 мин.)
После того, как каждый учащийся ответил на вопросы теоретической части и получил соответствующую оценку в карте ответа, все карты сдаются учителю и начинается зачёт по практике.
Каждый учащийся получает карточку с тестом , бланк ответа в форме таблицы и чистый лист для вычислений. В бланке ответа необходимо поставить крестик на пересечении выбранного задания и правильного варианта ответа.
Бланк ответов.
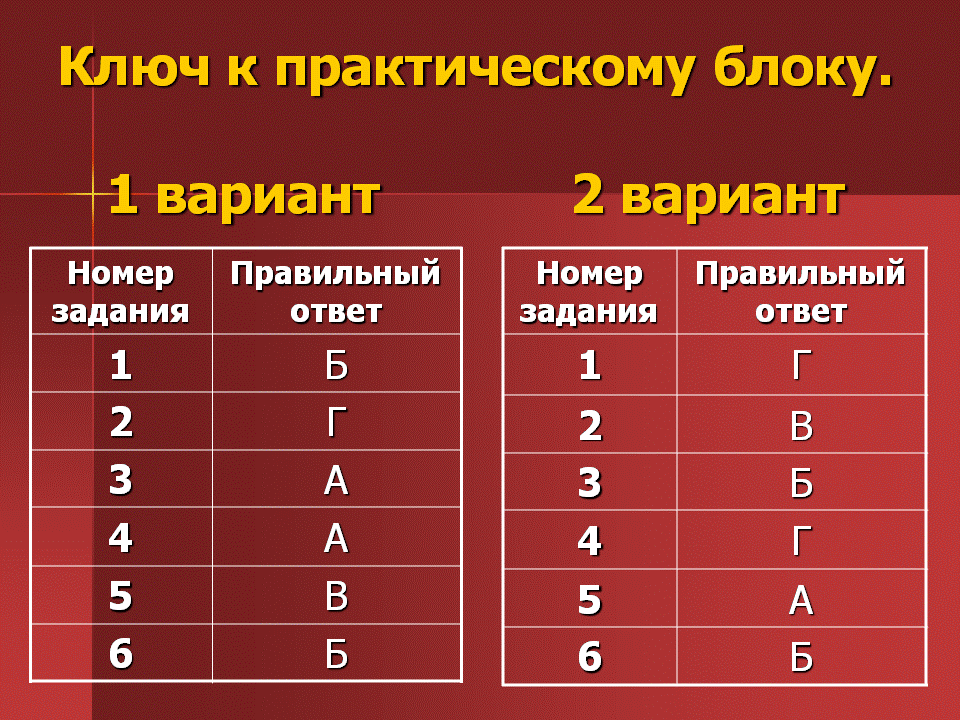
Критерий и ключ к практической части демонстрируется на интерактивной доске, после того, как учащиеся выполнили и сдали свою работу. В результате на конец урока каждый учащийся имеет полное представление о том, как он сдал зачёт. В случае недовольства полученной оценкой, каждый ученик имеет право пересдать зачёт в ближайшее, назначенное для него учителем время и повысить свою оценку.
| Варианты ответа | ||||
| А | Б | В | Г | |
| 1 | | | | |
| 2 | | | | |
| 3 | | | | |
| 4 | | | | |
| 5 | | | | |
| 6 | | | | |
Задания практической части.
| 2 вариант. №1. Найдите наименьшее значение функции №2. Найдите значение производной функции а) -2; б) 0; в) -6; г) 8. №3. Найдите наименьшее значение функции а) 18; б) -18; в) -24; г) 6. №4. Найти экстремумы функции : а) б) в) г) №5. Найдите производную функции g(x) = а) 1 №6. Найдите сумму корней уравнения (g(f(x)))' = 0, если f(x) = а) корней нет; б) 0; в) -2; г) 3. |
|
|
4 этап. Подведение итогов, обсуждение оценок. ( 3 мин.)
Здесь представлен конспект к уроку на тему «Производная», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.