Конспект урока «Производная сложной функции» по математике для 11 класса
Тема: “Производная сложной функции”.
Тип урока: – урок изучения нового материала.
Форма урока: применение информационных технологий.
Место урока в системе уроков по данному разделу: первый урок.
Цели:
-
научить распознавать сложные функции, уметь применять правила вычисления производных; совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером;
-
развивать готовность к информационно-учебной деятельности через применение информационных технологий.
-
воспитывать адаптивность к современным условиям обучения.
Оборудование: электронные файлы с печатным материалом, индивидуальные компьютеры.
Ход урока.
I. Организационный момент (1 мин.).
II. Постановка целей. Мотивация учащихся (1 мин.).
-
Обучающие цели: научиться распознавать сложные функции, знать правила дифференцирования, уметь применять формулу производной сложной функции при решении задач; совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером.
-
Развивающие цели: развивать познавательные интересы через применение информационных технологий.
-
Воспитательные цели: воспитывать адаптивность к современным условиям обучения.
III. Актуализация опорных знаний (5 мин.).
-
Дать определение производной функции.
-
Назовите правила вычисления производной.
3. Устная работа.
Найдите производные функций.
а) y = 2x2 + xі ;
б) f(x) = 3x2 – 7x + 5;
в) f(x) = ![]() ;
;
г) f(x) = 1/2x2;
д) f(x) = (2x – 5)(x + 3).
4. Правила вычисления производных.
Повторение формул по компьютеру со звуковым сопровождением.
IV. Программированный контроль (5 мин.).
| Вариант 1. | Вариант 2. | ||
| У = 2х + 5. | У = 2х – 5. | ||
| У = 4cos x. | у = 3sin x. | ||
| у = tg x + ctg x. | у = tg x – ctg x. | ||
| у = | у = | ||
| У = х2 +7х + 5 | У = 2х2 – 5х + 7 | ||
| Варианты ответов. | |||
| 1 | 2 | 3 | 4 |
| 2 | -2 | 5 | -5 |
| 4sin x | -4sin x | 3cos x | -3cos x |
| 1/cos2x + 1/sin2x | 1/cos2x – 1/sin2x | 1/sin2x – 1/cos2x | 1 |
| 1,6х0,6 + 2,5х1,5 | 2,6х0,6 + 1,5х1,5 | 1,5х0,5+ 4х3 | 2,5х0,5+ 4х3 |
| 2х + 7 | 2х +5 | 4х + 5 | 4х – 5 |
Обменяйтесь тетрадями. Отметьте в диагностических картах верно выполненные задания знаком +, а неверно выполненные задания знаком “–”.
V. Изучение нового материала (5 мин.).
Сложная функция.
Рассмотрим функцию, заданную формулой f(x) = ![]()
Для того, чтобы найти производную данной функции, надо сначала вычислить производную внутренней функции u= v(x) = xІ + 7x + 5, а затем вычисляют производную функции g(u) = ![]() .
.
Говорят, что функция f(x) – есть сложная функция, составленная из функций g и v, и пишут:
f(x) = g(v(x)).
Область определения сложной функции – множество всех тех х из области определения функции v , для которыхv(x) входит в область определения функции g.
ТЕОРЕМА.
Пусть сложная функция у = f(x) = g(v(x)) такова, что функция у = v(x) определена на промежутке U , а функция u = v(x) определена на промежутке Х и множество всех её значений входит в промежуток U. Пусть функция u = v(x) имеет производную в каждой точке внутри промежутка Х , а функция y = g(u) имеет производную в каждой точке внутри промежутка U. Тогда функция y = f(x) имеет производную в каждой точке внутри промежутка Х , вычисляемую по формуле
y'x = y'u • u'x.
Формулу читают так: производная y по x равна производной y по u, умноженной на производную u по x.
Формулу записывают ещё так:
f' (x) = g' (u) v' (x).
Доказательство.
В точке х ![]() Х зададим приращение аргумента
Х зададим приращение аргумента![]() , (х+
, (х+![]() х)
х) ![]() Х. Тогда функция u = v(x) получит приращение
Х. Тогда функция u = v(x) получит приращение ![]() , а функция y = g(u) получит приращение y. Надо учесть, что, так как функция u=v(x) в точке x имеет производную, то она непрерывна в этой точке и
, а функция y = g(u) получит приращение y. Надо учесть, что, так как функция u=v(x) в точке x имеет производную, то она непрерывна в этой точке и ![]() при
при ![]() .
.
При условии, что ![]() , имеем
, имеем
![]() получим
получим
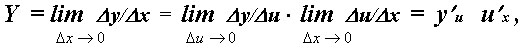
![]()
![]()
![]()
то есть формулу y' x = y' u · u'x .
VI. Закрепление изученного материала (11 мин.).
Применим полученную формулу для решения задач.
Пример 1.
Найти производную функции у = (1+х2)100.
Решение.
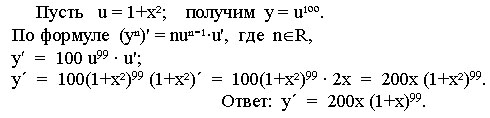
Пример 2 и Пример 3 из учебника (устно разобрать решение).
Решение примеров № 304, № 305, № 306 с последующей проверкой по компьютеру.
VII. Примеры для самостоятельного решения (8 мин.).
На рабочем столе компьютера.
Папка: “Производная сложной функции”. Документ: “Самостоятельная работа”.
-
у = (х2 – 3х + 1)3 – 1-я группа.
-
у = (1 + х – 2х2)10 – 1-я группа.
-
У = (
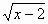 + 2)2 – 2-я группа.
+ 2)2 – 2-я группа. -
У = (2 –
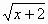 )2 – 2-я группа.
)2 – 2-я группа.
Проверка.
-
у' = (6х – 9)(х2 – 3х + 1).
-
у' = (10 – 40х)(1 + х – 2х2).
-
у' = 1 +
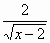
-
у' = 1 –
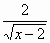
VIII. Индивидуальные задания (6,5 мин.).
На рабочем столе компьютера.
Папка: “Производная сложной функции”. Документ: “Индивидуальные задания”.
-
y = 2x + 3,6 sin5(p - x);
-
y = sin (2x2 – 3).
-
y = (1 + sin3x) cos3x;
-
y = tg x (tg x – 1).
IX. Итог урока (1 мин.).
-
Дать определение производной функции.
-
Назовите правила вычисления производных.
-
Какая функция является сложной?
-
Какова область определения сложной функции?
-
Назовите формулу нахождения производной сложной функции.
X. Задание на дом (0.5 мин.).
Здесь представлен конспект к уроку на тему «Производная сложной функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

