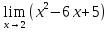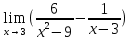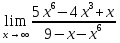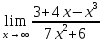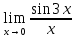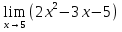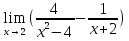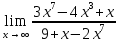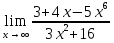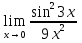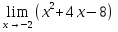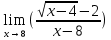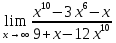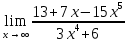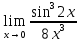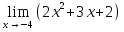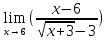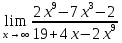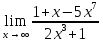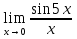Конспект урока «Вычисление пределов функции» по математике

План урока

Тема: «Вычисление пределов функции»

Тип урока – практическая работа.

Цель: закрепить и усовершенствовать практические приемы вычисления предела функции.

Задачи:

1. Формировать умения и навыки вычисления пределов;

2. Познакомить учащихся со способами раскрытия неопределенностей ( ;

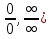3. Сформировать у учащихся навыки вычисления предела многочлена и отношения многочленов;

4. Сформировать у учащихся навыки применения первого и второго замечательных пределов для раскрытия неопределенностей ( ;

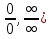5. Развивать мышление учащихся при выполнении упражнений;

6. Формировать умения и навыки самостоятельно умственного труда;

7. Способствовать воспитанию дисциплинированности, усидчивости, навыков самостоятельности и умения работать индивидуально.

Структура занятия:

1. Организационный момент (1-2 минуты)

2. Проверка домашнего задания (7-10 минут)

3. Сообщение темы занятия, актуализация опорных знаний (3-5 минут)

4. Формирование, закрепление первичных умений и применение их в стандартных ситуациях (40-45 минут)

5. Применение знаний и умений в измененных ситуациях (25минут)

6. Итог урока, рефлексия (3-4 минуты)

7. Задание на дом (1 минута)

Ход занятия

1. Организационный момент

Перед началом урока преподаватель проводит проверку подготовленности кабинета к занятию.

Приветствие учащихся, определение отсутствующих, заполнение группового журнала.

2. Проверка домашнего задания:

Выясняет, были ли сложности с выполнением домашнего задания. При необходимости отвечает на вопросы учащихся. Просит некоторых учащихся сдать тетради для проверки домашнего задания.

3. Сообщение темы занятия, актуализация опорных знаний

Сообщается тему урока: «Вычисление пределов». Вместе с учащимися формулирует цель урока.

Прежде чем начать вычислять значения пределов функции, просит учащихся дать определение предела функции и вспомнить основные свойства пределов.

Число b называется пределом функции f(x) в точке a, если для всех значений x, достаточно близких к а и отличных от а, значения функции f(x) сколь угодно мало отличаются от числа b.

Основные свойства пределов:

1. Предел алгебраической суммы конечного числа переменных величин равен алгебраической сумме пределов слагаемых;

2. Предел произведения конечного числа переменных величин равен произведению их пределов;

3. Постоянный множитель можно выносить за знак предела;

4. Предел отношения двух переменных величин равен отношению пределов, если предел знаменателя не равен 0;

5. Предел положительной степени переменной величины равен той же степени предела этой же переменной;

6. Если переменные x,y,z удовлетворяют неравенствам xyz и x->a, z->a, то и y->a.

4. Формирование, закрепление первичных умений и применение их в стандартных ситуациях:

Сначала рассмотрим примеры непосредственного нахождения предела функции в точке.

№120. Найти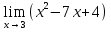

Решение. Для нахождения предела данной функции заменим аргумент x его предельным значением:

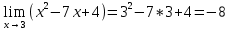
№121. Найти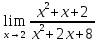

Решение. Проверим, не обращается ли знаменатель дроби в нуль при x=2: имеем 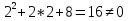. Подставив предельное значение аргумента, находим

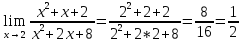
Рассмотрим теперь такие примеры, когда применение свойств предела становится возможным лишь после некоторых предварительных преобразований.

№122. Найти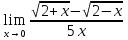

Решение. Здесь пределы числителя и знаменателя при x0 равны 0. Умножив числитель и знаменатель на выражение, сопряженное числителю, получим

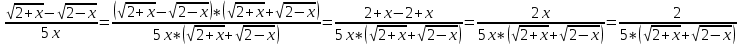
Следовательно,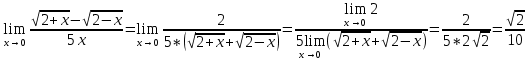

№123. Найти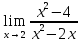

Решение. Здесь имеем неопределенность 0/0. Для того чтобы раскрыть эту неопределенность, разложим числитель и знаменатель дроби на множители и до перехода к пределу сократим дробь на множитель х-2. В результате получим

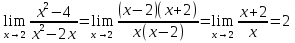
Итак, чтобы найти предел частного двух функций, где пределы делимого и делителя равны 0, нужно преобразовать функцию таким образом, чтобы выделить в делимом и делителе сомножитель, предел которого равен 0, и, сократив дробь на этом сомножитель, найти предел частного.

№124. Найти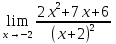

Решение. Здесь имеем неопределенность 0/0. Для того чтобы раскрыть эту неопределенность, разложим числитель на множители и до перехода к пределу сократим дробь на множитель х+2.

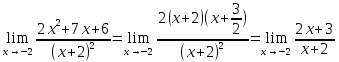
Здесь предел делителя равен 0. Таким образом, знаменатель дроби неограниченно убывает и стремиться к 0, а числитель приближается к -1. Ясно, что вся дробь неограниченно растет, что условно записывается так: .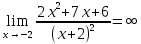

Перейдем к примерам нахождения предела функции на бесконечности.

№131. Найти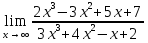

Решение. При x->∞ имеем неопределенность вида ∞/∞. Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель на x³.Тогда получим

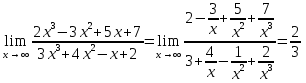
№134. Найти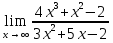

Решение. Разделив числитель и знаменатель на x³ и перейдя к пределу, получим

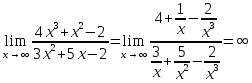
поскольку числитель последней дроби стремиться к пределу, отличному от нуля, а знаменатель – к нулю.

№135. Найти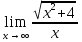

Решение. При стремлении аргумента x к бесконечности имеем неопределенность вида ∞/∞. Чтобы раскрыть ее, разделим числитель и знаменатель дроби на x. Тогда получим

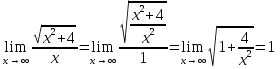
№136. Найти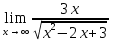

Решение. Предельный переход 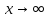всегда можно заменить предельным переходом при 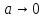, если положить а=1/x (способ замены переменной). Так, полагая в данном случае x=1/а, найдем, что 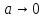при 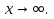Следовательно,

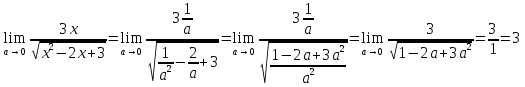
№137. Найти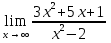

Решение. 1 способ. Разделив числитель и знаменатель на x², находим

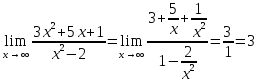
2 способ. Положим x=1/а; тогда что 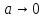при 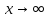. Значит

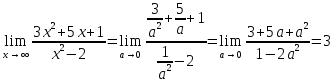
№142. Найти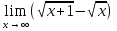

Решение. Здесь требуется найти предел разности двух величин, стремящихся к бесконечности (неопределенность вида ∞-∞). Умножив и разделив данное выражение на сопряженное ему, получим

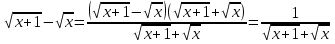
Следовательно .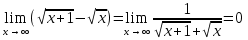

Рассмотрим примеры, в которых используются замечательные пределы.

№ 143. Найти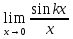

Решение. Произведем подстановку kx=y. Отсюда следует, что 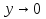при 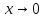, а x=y/k. Тогда получим

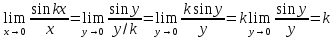
Так как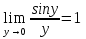

№ 144. Найти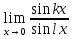

Решение. Имеем

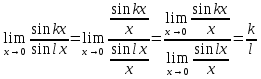
Здесь мы разделили числитель и знаменатель дроби на x (это можно сделать, так как 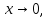но x0), а затем воспользовались результатом предыдущего примера.

№ 145. Найти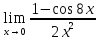

Решение. Преобразуем числитель к виду 1-cos8x=2sin²4x. Далее находим

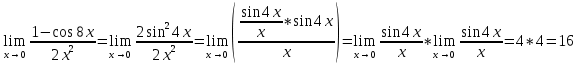
№ 146. Найти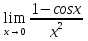

Решение. 1 способ. Здесь имеет место неопределенность вида 0/0. Применяя известную тригонометрическую формулу и выполняя элементарные преобразования, получим

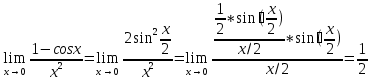
2 способ. Преобразуем числитель следующим образом:

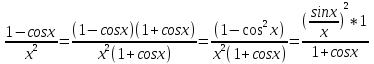
Следовательно,

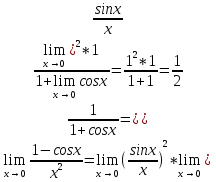
№ 147. Найти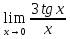

Решение. Заменив tg x на sin x/cos x, получим

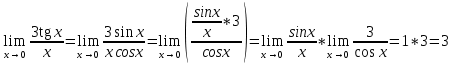
№ 154. Найти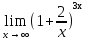

Решение. Имеем

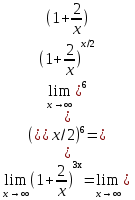
Положим x/2=y. Тогда при неограниченном возрастании x переменная y также будет неограниченно возрастать. Поэтому, используя второй замечательный предел, получим 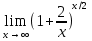= 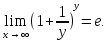Итак, .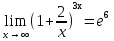

№ 155. Найти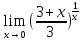

Решение. Запишем основание степени в виде 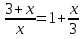, а показатель степени – в виде 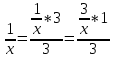. Следовательно,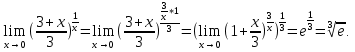

№ 156. Найти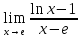

Решение. Имеем

=

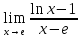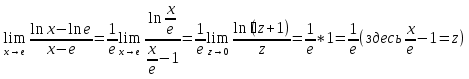
5. Применение знаний и умений в измененных ситуациях:

Предлагает учащимся выполнить самостоятельную работу (4 варианта, см. приложение).

6. Подведение итогов урока, рефлексия

Объявляет итог урока, называет оценки.

В качестве рефлексии учащимся предлагается закончить предложения и высказать свои мнения.

Данное занятие для меня…

Я почувствовал(а), что…

В будущем я…

Сегодня работать для меня было…

Мне бы хотелось изменить…

На следующем занятии мне бы хотелось…

7.Задание на дом

[2, стр.180], №130, №133, №140, №151, №158.

ПРИЛОЖЕНИЕ

Самостоятельная работа

Вычисление пределов

Вариант – 1