Конспект урока «Вычисление производных» по математике
Краевое государственное бюджетное профессиональное
образовательное учреждение
«Спасский политехнический колледж»
Методическая разработка открытого урока.
Предмет: Математика.
Тема: Вычисление производных.

2014 год
Цели урока:
Обобщить и оценить знания учащихся по данной теме:
-
Проверить умения учащихся применять формулы и правила вычисления производных.
-
Развивать мышление, речь, умение комментировать, тренировать память.
-
Воспитывать трудолюбие, чувство товарищества и взаимопомощи.
-
Прививать интерес к предмету путем дружеского соперничества в командах
Методы и приемы: словесный, наглядный.
По типу: урок обобщения и систематизации знаний.
Оборудование: раздаточный материал (разноуровневые карточки с практическими заданиями, листы учета знаний), плакаты с теоретическим материалом в схемах и таблицах, карточки с основными формулами.
Ход урока
1 ЭТАП. Организационный момент
Эпиграфом к сегодняшнему уроку будут слова Ньютона “При изучении наук примеры не менее поучительны, нежели правила” и слова Ломоносова “Примеры учат больше, чем теория”.
К этим словам мы вернемся позднее. Группа разбивается на три разноуровневые группы (причем ребята сами оценивают свои знания и выбирают группу). Капитан каждой группы получает памятку по оценки заданий и карточку с таблицей, в которую он будет выставлять баллы после каждого задания всем членам команды.
2 ЭТАП. Комбинированная работа
(работа у доски, работа по карточкам, устная и письменная работа с классом)
Разминка
-
Представитель каждой команды вытягивает некоторую записанную букву алфавита. За три минуты придумать математические термины, начинающиеся на эту букву.За каждый названный термин команда получает один балл.
-
Если группа сформулирует определение, то получает дополнительно еще три балла. Если группа не может сформулировать определение, то другие группы получают возможность заработать дополнительно три балла, сформулировав это определение.
Работа у доски (к доске вызываются трое учащихся):
Вычислить производную:
а) у = 4х2 + 5х + 8
б) у = (2х – 1)3 и найти их значение в точке х0 = 2.
Найти значения переменной х, при которых верно равенство:
а) sin' х = (х – 5)'
б) (2cos x)' = (![]() х + 7)'
х + 7)'
Вычислить производную: у = ![]()
 Работа по карточкам (разноуровневая работа, выполняется учащимися на местах):
Работа по карточкам (разноуровневая работа, выполняется учащимися на местах):
Карточка №1 (уровень А).
Найдите производную функции:
-
у = 5 – 7х
-
у = (х – 5)(2х – 5)
-
у =
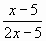
Карточка №2 (уровень В).
Найдите производную функции:
-
у = (х3 – 2х2 + 5)6;
-
у = cos(х3-3)
-
у =
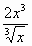 у =
у = 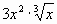
Карточка №3 (уровень С).
Найдите производную функции:
-
у = sin3 5x
-
y =
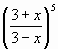
-
y =
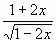
Карточка №4 (уровень А).
Найдите производную функции:
-
у = cos x + ctg x
-
y = 5 sin 3x
-
y = 4x5 + tg 3x – cos2x
Устная работа с классом
Вычислить производную:
-
у = 2х – 3
-
у = х2 – 3х + 4
-
у = 3 cosx
-
у = sin5x
-
у = tg(2 – 5х)
-
у = arcsin2х
-
у = (х – 3)2
-
у = (3 – 4х)2
2 Дана функция f(x) = 4х2. Вычислить f '(1), f '(-2).
3 Дана функция f(x) = х3. Решите уравнение: f(x) = f '(х).
Письменная работа с классом
Решить уравнение: ((41 – 5х)2)' = х0, где х0 – корень уравнения ![]() .
.
3 ЭТАП. Работа по группам
Каждая команда получает карточки с заданиями разного уровня сложности.
По одному человеку от команды решают у доски, остальные в тетрадях.
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
-
у = 4х4 -
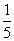 х5 + х2 -3х
х5 + х2 -3х -
у = (х + 4)3 у =
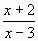
-
Вычислите у '
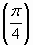 , если у(х) = ctgx – tgx.
, если у(х) = ctgx – tgx. -
Решите уравнение: f ' (x) = 0, если f (x) = х4 - 2х2 + 1

Карточка №2 (уровень сложности В)
1 Найдите производную функции:
-
у = -
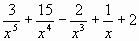
-
у = sin(2х2 + 3)
-
у =
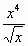
-
у = cos3x
-
Вычислите у ' (600), если у(х) =
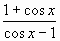
-
Решите уравнение: f ' (x) = 0, если f (x) = -
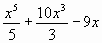
-
Дополнительно. Решить уравнение | х + 2 | + | х – 3 | = 5
Карточка №3 (уровень сложности С)
Найдите производную функции:
-
у =
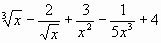
-
у = (х2 + 6)
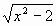
-
у =
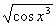
-
у = arctg 2x
-
Вычислите у '
 , если у(х) = sin x · cos2 x
, если у(х) = sin x · cos2 x -
Решите уравнение: f ' (x) = 0, если f (x) = x – tg x
-
Дополнительно. Решить неравенство у ' > 0, если у(х) = (3х – 1)10 · (2х + 5)7.
4 ЭТАП. Соревнование по группам
На доске записаны задания трех уровней сложности. Каждая группа выбирает свой уровень и выполняет задания в группе на местах, распределяя задания на каждого ученика группы. Каждому заданию соответствует некоторая буква.
Выигрывает та команда, которая вперед угадывает слово.
Вычислить производную:
| Задание | |
| А | у = 4х3 – 2х2 + х – 5 |
| В | у = (х3 – 1)(х2 + х + 1) |
| С | у = |
| А | у = (х2 -5х + 8)6 |
| В | у = |
| С | у = |
| А | у = sin (4х – 1) |
| В | у = sin2 |
| С | у = |
| А | у = |
| В | у = |
| С | у = |
| А | у = tg x – x |
| В | у = arcsin 2x |
| С | у = arctg(2x2 – 5) |
| А | у = arccos x |
| В | у = sec 2x |
| С | у = sin2 x · cos x |
Шифры:
| Соответствующая буква | |
| 12х2 – 4х + 1 | а |
| 6х5 + 4х3 + 3х2 – 2х – 1 | а |
| - | т |
| - | и |
| - | м |
| - | е |
| - | т |
|
| з |
|
| и |
| 2 tg 2x · sec 2x | м |
|
| и |
|
| м |
| 6(х2 – 5х + 8)(2х – 5) | т |
|
| а |
|
| е |
| 4 cos (4x – 1) | е |
|
| з |
|
| з |
Задания, с которыми не справились группы, решаются совместно, обосновываются выводы.
Капитан оценивает работу каждого по следующим критериям:
-
решил сам без ошибок и помог товарищу – 5 баллов
-
решил сам, но консультировался у товарища – 4 балла
-
решал с помощью карточки с формулами и учителя – 3 балла
5 ЭТАП. Итог урока
1. Самооценка труда учащихся.
-
Выполнил ли программу урока полностью;
-
Какие виды работ вызвали затруднения и требуют повторения;
-
В каких знаниях уверен.
2. Оценка труда товарищей:
-
Кто, по-вашему мнению, внес наибольший вклад;
-
Кому, над чем следовало бы еще поработать.
3. Оценка работы класса учителем.

6 ЭТАП. Домашнее задание: составить проверочную карточку из трех заданий по данной теме (разноуровневую)
Здесь представлен конспект к уроку на тему «Вычисление производных», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.