Конспект урока «Вычисление углов между скрещивающимися прямыми» по математике для 11 класса

Конспект урока по математике

для учащихся 11 класса

«Вычисление углов между скрещивающимися прямыми»

(Подготовка к ЕГЭ)

Автор:

Учитель математики МОУ «СОШ № 55»

Ленинского района города Саратова

ПЕТРОВА Людмила Дмитриевна

Тип урока: урок обобщения и систематизации знаний.

Урок одной задачи по тему:
«Угол между скрещивающимися прямыми».

1. Характеристика темы урока.
   1) Центральным моментом технологии подготовки к ЕГЭ является обучение школьника приёмам мысленного поиска способа решения, а для этого следует показать ему всю картину поиска в трудных заданиях.
   2) Решение задачи по стереометрии, планиметрии оформляются примерно одинаково. В основе лежат общематематические и даже, можно сказать, общенаучные принципы.
   Структура текста решения такова: оно разделяется на этапы, а те, в свою очередь, могут быть разбиты на более мелкие части, содержащие цепочки умозаключений: как правило, следствий, равенств и даже неравенств, в зависимости от постановки и содержания задачи.
   3) Особая роль при решении геометрической задачи отводится чертежу, он не обязательно должен быть ровно один. Обычно на нём, в соответствии с условием задачи отмечают следующие данные:
   а) обозначения точек, прямых, плоскостей и других геометрических объектов;
   б) длины отрезков, величины углов, площади и объёмы;
   в) соотношения равенства длин или углов, перпендикулярности прямых или плоскостей.
   На чертеже можно ещё и вводить новые:
   а) обозначения объектов – первоначальных или возникающих в процессе дополнительных построений;
   б) величины – буквенные или вычисленные в процессе решения;
   в) соотношения равенства или перпендикулярности, определяемые построением или выведенные с помощью рассуждений.
   Одним словом, на чертеже фактически можно решать задачу, или, по крайней мере, демонстрировать фрагменты её решения.
   4) В связи с возможностью решать задачу прямо на чертеже возникают некоторые ограничения и проблемы.
   Ученику необходимо побеспокоится о том, чтобы проверяющий смог понять, в каком порядке и на основании чего появились на чертеже новые пометки. С этой целью пишется текст решения, который хотя и дублирует отчасти чертёж, тем не менее, отличается большей содержательностью, т.к. в нём :
   а) отражается хронология проведённых умозаключений;
   б) указываются причинно-следственные связи между утверждениями.
   Чертёж должен быть абсолютно ясным и разборчивым, а главное, понятным.
   Укажем типы задач по стереометрии, встречающиеся на ЕГЭ и вызывающие определённые трудности.
   1. Угол между скрещивающимися прямыми
   2. Расстояние от точки до прямой, до плоскости, расстояние между скрещивающимися прямыми.
   3. Угол прямой с плоскостью.
   4. Угол между плоскостями.

2. Цели урока.

1. Методическая цель урока.
   Показать приёмы формирования у школьников навыков решения задач на вычисление углов в пространстве, умения применять изученный теоретический материал на практике, развивать их самостоятельность при решении задач разными методами.
   Методы:

А) использование моделей фигур и интерпретация их на чертеже;

Б) отбор соответствующих задач, способствующих формированию навыков и умений учащихся;

В) рассмотрение различных способов решения одной задачи.

2) Образовательная цель урока.
Рассмотреть 3 метода решения одной задачи на вычисление угла между скрещивающимися прямыми.
3) Воспитательные цели урока.
Формирование мировоззрения: показать, что источник возникновения изучаемых понятий представляет собой определённую систему знаний в геометрии.

III. На доске девиз.

«Незнанием никогда не следует
хвалиться: незнание есть бессилие».
- Н. Г. Чернышевский.

Сегодня на уроке при решении одной задачи на вычисление угла между скрещивающимися прямыми мы рассмотрим 3 метода решения.
Методы:
1. Поэтапно-вычислительный
2. Векторно-координатный
3. Геометрический

Задача.
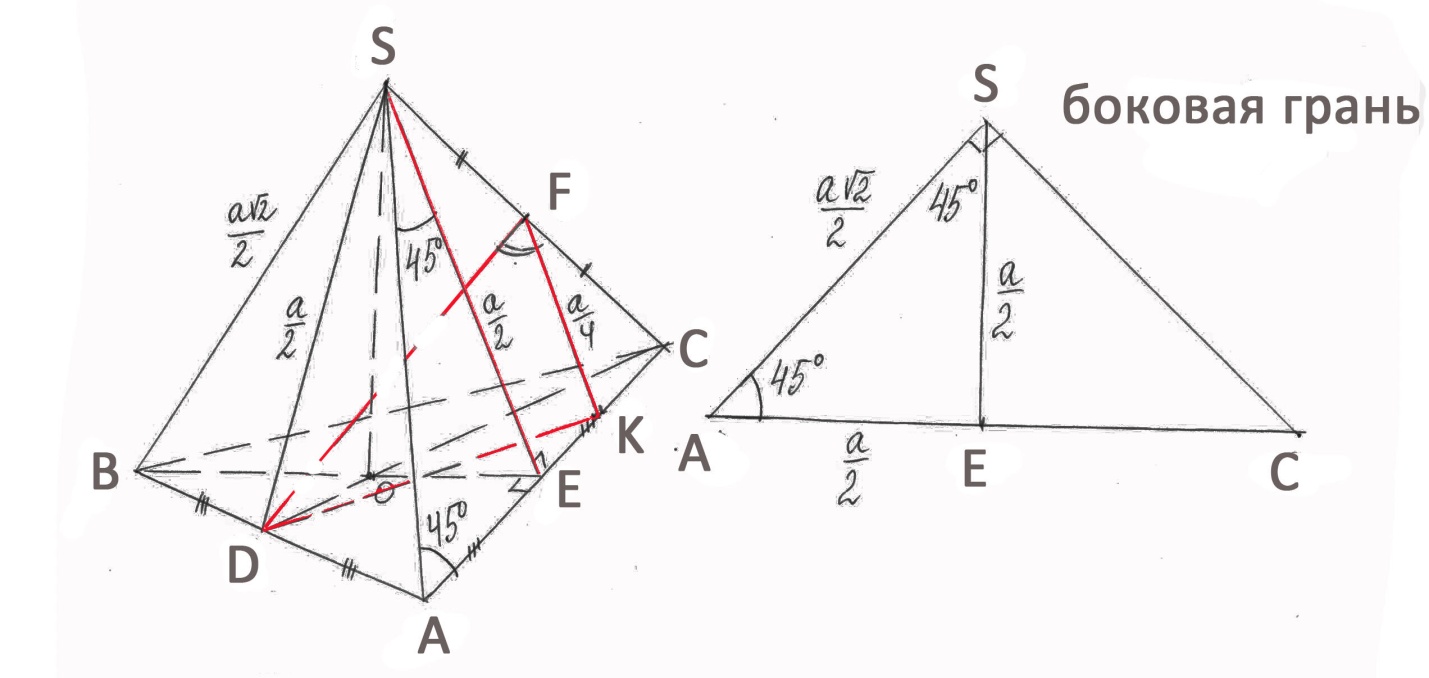
На ребрах АВ, АС и SC правильной треугольной пирамиды SABC, у которой все плоские углы при вершине S прямые, взяты соответственно точки D, E, F – середины этих рёбер. Найти угол между прямыми DF и SE.

Решение.

1. Поэтапно вычислительный метод.

1. Построение чертежа.

2. Угол между прямыми DF и SE – искомый. DF и SE – скрещивающиеся прямые, т.к. SE лежит в плоскости ASC, а прямая пересекает эту плоскость в точке F, не лежащей на прямой SE.

3. Построим какой-нибудь угол, равный искомому. Для этого в плоскости SAC, которая проходит через прямую SE (одну из скрещивающихся прямых) и точку F (на другой скрещивающейся прямой), через т. F проведём прямую FK||SE.
   DFK равен искомому. Пусть DFK = .

4. Угол  поместим в некоторый треугольник, для чего проведём DK.  - угол треугольника DFK.

5. Найдём стороны треугольника DFK.
   а) введём вспомогательный параметр: обозначим сторону основания через ;
   б) треугольник ASC – прямоугольный равнобедренный, SE – медиана; SE = AE = .
   FK – средняя линия треугольника SEC, FK = .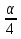

в) Найдём DF из треугольника SDF.
Определим вид этого треугольника.
По условию BSA, BSC, ASC – прямые.
Следовательно,
SCSB SC  (BSA)
SCSA по признаку.

Аналогично,
SD  (BSA) SC  SD по
SC  (BSA) определению.
Следовательно, 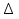DSC – прямоугольный, и 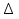DSF тоже прямоугольный.
г) SF = 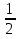SC = () =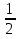

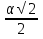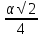
д) По теореме Пифагора DF = = = = = = .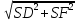

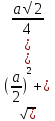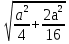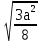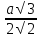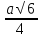DF = .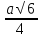

e) По теореме косинусов:
DK² = AD² + AK² – 2DA  AK  cosA = (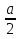)² 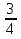 (a)² – 2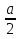 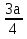   cos60 = + - + .

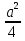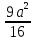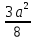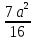DK = = .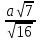

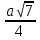6. Из :
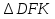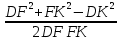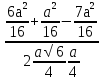   cos = = = 0.
   =90

2. Векторно – координатный метод.
   
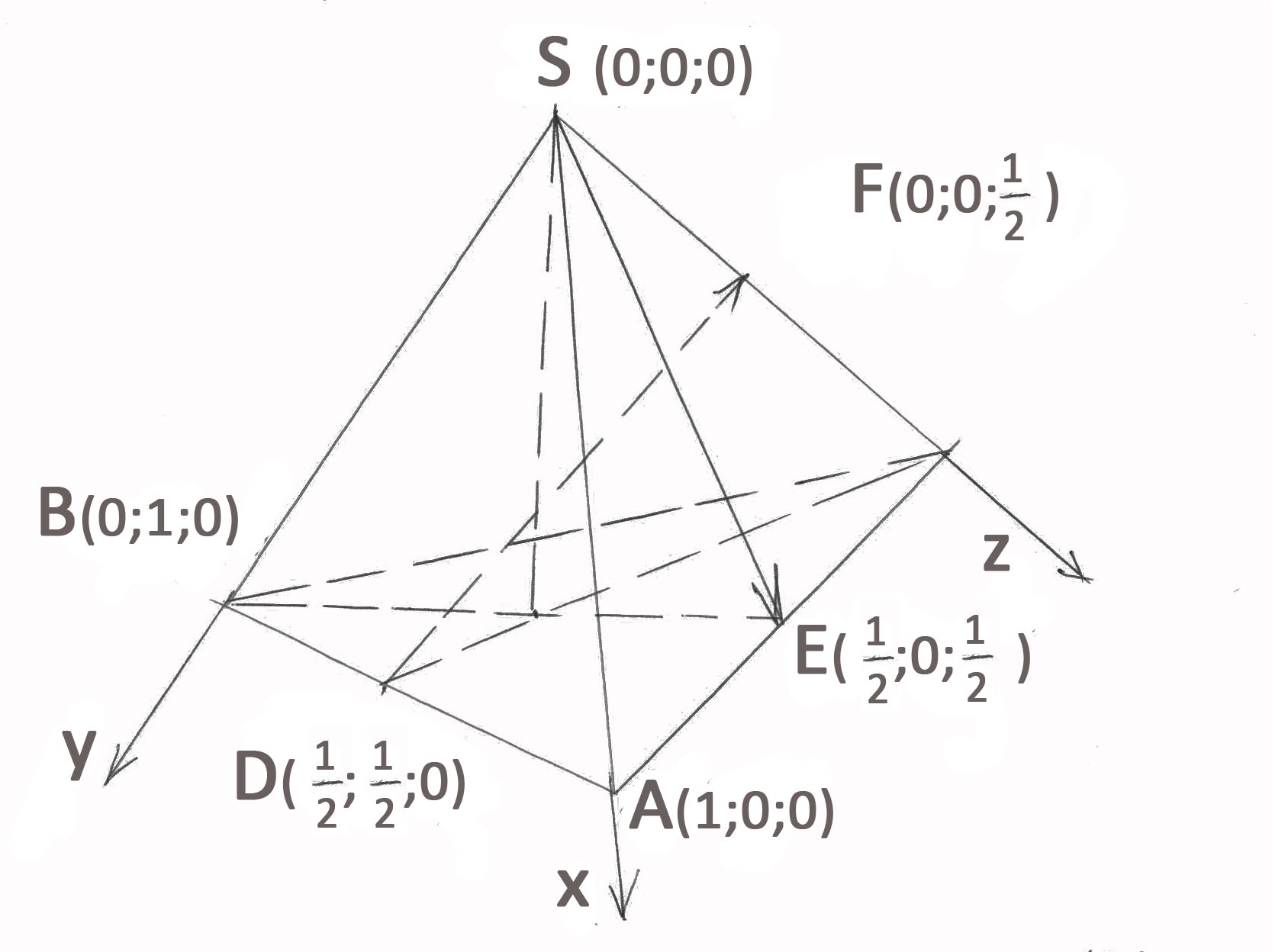
   Т.к. заданная пирамида правильная, то SA=SC=SB. По условию все углы при вершине S прямые. Поэтому: 1) введём в пространстве прямоугольную систему координат: начало – точка S; отрезки SB, SA, SC – единичные отрезки соответствующих осей Sx, Sy, Sz.
   2) Определим координаты точек S, A, B, C, D, E, F.
   3) {; }, {}.
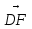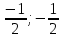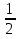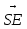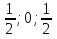   4) cos (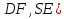= |cos( 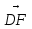, 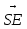)| = = 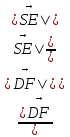= 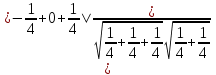0.
   
   =90

3. Геометрический метод.
   
   
   
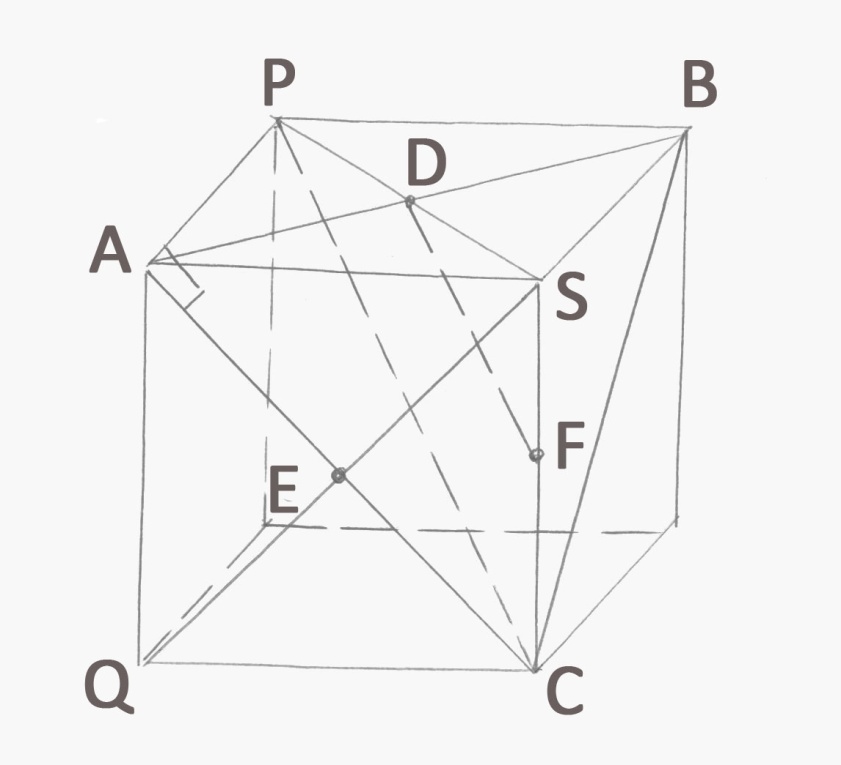
   Т.к. отрезки SA, SB, SC равны между собой и попарно перпендикулярны, то можно принять их за рёбра куба, выходящие из одной вершины.
   Построим этот куб и заданные точки D, E, F.
   1) Соединим вершины P и С куба и проведём диагональ SQ.
   2) Нетрудно убедиться, что DF||PC (средняя линия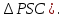
   3) Угол между прямыми SE и DF равен углу между PC и SQ.
   4) АС – проекция прямой РС на плоскость ASC.
   АСSQ (свойство диагоналей квадрата)
   РСSQ (теорема о трёх перпендикулярах)
   Следовательно, DFSQ и тогда DFSE, т.е. угол равен 90.

4. Итог урока.
   На примере одной задачи мы рассмотрели 3 различных метода решения. Можно сказать, что эффективность каждого метода зависит конкретно от предлагаемой задачи. Какой метод выбрать зависит от вас, вашей математической подготовки и опыта, т.е. количества решенных вами задач. Вы убедились, какой большой теоретический материал необходим для решения задачи.

Наш урок я хочу закончить словами:
«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию»
- Ян-Амос Каменский

5. Домашнее задание. Задачи на стенде.

1. В правильной пирамиде SABC отношение бокового ребра к стороне основания равно 2:1. На рёбрах АВ и АС взяты соответственно точки М и К – середины этих рёбер. Найти угол между прямыми SM и ВК.

2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ угол между прямыми B₁D и CD₁ равен 90 и АВ:AD = 1:2. Найти угол между прямыми АС и А₁D.

3. На рёбрах ВВ₁ и С₁D₁ куба ABCDA₁B₁C₁D₁ взяты соответственно точки Р и Q такие, что ВР:ВВ₁=2:3, С₁Q : C₁D₁ = 1:4. Плоскость, проходящая через точки A, P, Q, пересекает прямые DD₁ и B₁C₁ соответственно в точках E и F. Найти угол между прямыми EF и А₁С.

4. В основании пирамиды лежит параллелограмм ABCD, угол BAD которого равен 45, а отношение сторон АВ:АD = 1:2. Грань SAB является равносторонним треугольником, а её медиана SF перпендикулярна плоскости основания. На ребре SC взята точка М, такая что SМ:SC = 2:3. Найти угол между прямыми SF и DM.