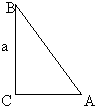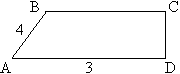Конспект урока «Соотношения между сторонами и углами прямоугольного треугольника» по математике для 8 класса
 Соотношения между сторонами и углами прямоугольного треугольника (8-й класс)
Соотношения между сторонами и углами прямоугольного треугольника (8-й класс)
Цели:
-
Совершенствовать навыки решения прямоугольных треугольников.
-
Развивать познавательный интерес к предмету.
-
Воспитывать ответственность, целенаправленность при решении задач.
Ход урока
1. Организационная часть
Учитель: Сегодня мы с вами отправимся в путешествие, будем покорять Уральские горы, а конкретно гору Народная, высота которой достигает 1895 метров. И цель не сам полет, а добыча новых знаний. Как в любом путешествии мы должны определить свой маршрут. Добираться будем самолетом до Воркуты, а далее в горы пешим ходом, но для начала приобретем билеты и рюкзаки с необходимыми припасами еды.
2. Проверка знаний
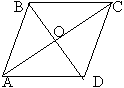
а) Домашнее задание № 601. Найти углы ромба, если его диагонали равны 2![]() 3 и 2.
3 и 2.
| Дано: ABCD-ромб, АС=2 Решение: 1) из tg OBC = OC\BO = 2) Диагонали ромба делят углы, из которых исходят пополам.
|
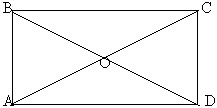
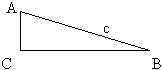
№ 602. Стороны прямоугольника равны 3 см и ![]() 3 см. Найдите углы, которые образует диагональ со сторонами прямоугольника.
3 см. Найдите углы, которые образует диагональ со сторонами прямоугольника.
| Решение:
|
б) Блицтурнир. Ответы даются быстро. Наивысшая оценка 5 баллов- цена билета на самолет.
|
|
| |
| 2) |
|
|
| 3) | sin | |
| 4) |
|
|
| 5) |
|
|
3. Решение задач
– Ребята, за нами осталось покорение вершины и установление флага на самой высокой точке Уральских гор.
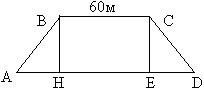
1. № 600. Насыпь шоссейной дороги имеет в верхней части ширину 60 м. Какова ширина насыпи в нижней её части, если угол наклона откосов к горизонту равен 60°, а высота насыпи равна 12 м.
| Наводящие вопросы: Дано: Найти: AD |
Решение:
1) из ![]() ABH tg60° =BH/AH AH=BH/tg60° =12/
ABH tg60° =BH/AH AH=BH/tg60° =12/![]() 3 = 4
3 = 4![]() 3 м.
3 м.
2) ![]() ABH =
ABH = ![]() CDE по катету и одному углу, то AH = ED = 4
CDE по катету и одному углу, то AH = ED = 4![]() 3м
3м
3) HBCE –прямоугольник, то BC=HE=60м.
4) AD= 4![]() 3+4
3+4![]() 3 +60 = 60 +8
3 +60 = 60 +8![]() 3 м.
3 м.
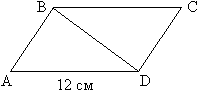
2. № 603
| Дано: Найти: Sпар. |
Наводящие вопросы:
-
Как находится площадь параллелограмма?
-
Как находится площадь прямоугольного треугольника?
-
Как найдем площадь параллелограмма?
Решение:
1) ![]() ABD прямоугольный.
ABD прямоугольный.
cosA = AB/AD, то AB = AD * cosA = 12 * cos47° 50![]() = 12 * 0,6713 = 8,1 см
= 12 * 0,6713 = 8,1 см
2) sinA = BD/AD, то BD = AD * sinA = 12 * sin47° 50![]() = 12 * 0,7412 = 8,9 см
= 12 * 0,7412 = 8,9 см
3) S![]() ABD = 1\2 * 8,1 * 8,9 = 36 cм2
ABD = 1\2 * 8,1 * 8,9 = 36 cм2
4) S =2 * 36 = 72 см2
4. Физкультминутка
5. Самостоятельная работа
Возвращаемся домой, в рюкзаках у нас самородки – драгоценные камни, а пока мы летим в самолете домой – решим самостоятельно задачи. Счастливой посадки.
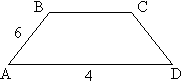
| II вариант | |
| 1) sin | 1) cos |
| Найти AD, CD, площадь трапеции | Найти AD, высоту и площадь трапеции. |
|
|
|
6. Домашнее задание
п.66, 67(правила), №598, №599.
Здесь представлен конспект к уроку на тему «Соотношения между сторонами и углами прямоугольного треугольника», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.